椭圆曲线公钥密码学习

一、         密码背景

基于有限域上离散对数问题的公钥密码体制，最著名的是ElGamal体制，是由T. ElGamal在1985年提出的 ElGamal有较好的安全性，同一明文在不同时刻会产生不同的密文应用广泛，尤其数字签名方面的应用，著明的美国数字签名标准DSS就是ElGamal的一种变形。

二、         加解密算法

加密过程：

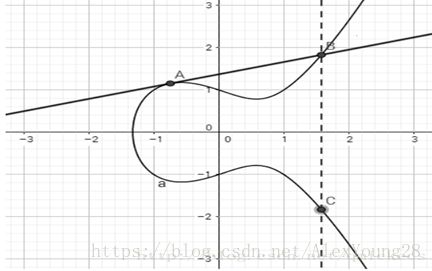
(1)   A将明文消息编码成一个数m

(2)   在区间[1,n-1]内，A选取一个随机数k，计算点P1：P1=(x1,y1)=Kg;

(3)   依据接收方B的公钥，A计算点=(x2,y2)=k;

(4)  A计算密文C=m

(5)  A传送加密数据{Kg,,C}给接收方B；

解密过程：

(1)   接受方B收到加密数据={Kg,,C};

(2)   接受方B使用自己的私钥作如下计算：

 

(3)   B计算m=(C-)/x，得明文m。

三、         椭圆曲线公钥密码算法数论基础

中学的时候我们学过圆锥曲线，比如椭圆、双曲线和抛物线。因为描述这些曲线的方程都是二次方程，圆锥曲线又被称为二次曲线。而椭圆曲线是则是由三次方程描述的一些曲线。更准确地说，椭圆曲线是由下面的方程描述的曲线：

 

y2=x3+ax+b其中4a3+27b2≠0

 

需要注意的是，椭圆曲线之所以叫“椭圆曲线”，是因为其曲线方程跟利用微积分计算椭圆周长的公式相似。实际上它的图像跟椭圆完全不搭边。

下图是椭圆曲线y2=x3−x+1的图像

 

 

 

椭圆曲线有这样的两个性质：

关于X轴对称

画一条直线跟椭圆曲线相交，它们最多有三个交点

  

  椭圆曲线上的运算：

  由于椭圆曲线加密进行的运算实际上都是在椭圆曲线上进行的，所以接下来需要定义一些椭圆曲线上的运算。

必须注意的是，这里把这些运算称为“加法”和“乘法”仅仅是方便描述，他们跟平时认知的加法和乘法完全是两码事，完全可以给他们取其它名字（比如”乘法“和”幂运算“等）。

首先定义坐标系中距离X轴无穷远点为椭圆曲线上的一个特殊点，称为0点。

那么此时上述第二条性质可以加强为：过曲线上任意两点（可重合）的直线必定与曲线相交于第三点。

然后定义椭圆曲线上点的加法。设椭圆曲线上有两点，A和B点，那么作过这两点的直线与该曲线相交于第三点（C点），然后关于X轴对称得到D点，则D为这两个点的和，记作D=A+B。很明显，D点也在该曲线上。所以椭圆曲线上两点之和也是曲线上的点。

特别地，如果两点重合，则作椭圆曲线在A点处的切线，与曲线相交于第二点（B点），然后关于X轴对称得到C点，则C点为A点与自身的和，记作C=A+A

那么关于这个加法，我们可以得到以下结论：

A+B=B+A

也就是椭圆曲线上的加法满足交换律。

A+0=A

因为0点是无穷远点，所以过A点与0点的直线是垂直于X轴的，它与曲线相交于另一点B点，那么B点关于X轴对称的点就是A点，即A点为A点和0点之和。

然后在加法的基础上，定义椭圆曲线上点的乘法。

设P是椭圆曲线上的一个点，那么正整数k乘以点P的结果由下面的式子定义，注意式子中的加法是上面提到的椭圆曲线上点的加法：

1∗P=P

2∗P=P+P

3∗P=2∗P+P

…

k∗P=(k−1)∗P+P

这个乘法满足以下性质：

对于任意正整数k和j，有

k∗(j∗P)=(kj)∗P=(jk)∗P=j∗(k∗P)

   

椭圆曲线上的离散对数问题:

定义了基本的加法和乘法运算后，我们可以由此得到椭圆曲线加密依赖的数学难题。

 

k为正整数，P是椭圆曲线上的点（称为基点），已知k∗P和P，计算k

从程序实现的角度来考虑，假设有这么一个函数：

 Point add(Point A, Point B) {...}

函数参数是两个椭圆曲线上的点，返回值是过两个点的直线与椭圆曲线相交的第三个点关于X轴对称的点。

那么按照如下方式调用函数：

 

Point result =P;

for (int i = 0;i < k - 1; i++)

    result = add(P, result);

sendTo((result,P), others);

如果别人只知道result和P点，是很难求出k的值是多少的。

 

如果我们改一种记法，把椭圆曲线上点的加法记作乘法，原来的乘法就变成了幂运算，那么上述难题的形式跟离散对数问题应该是一致的。即：

k为正整数，P是椭圆曲线上的点，已知Pk和P，计算k=logPPk。

所以这个难题叫椭圆曲线上的离散对数问题。

尽管两者形式一致，但是他们并不等价。实际上这个问题比大整数质因子分解（RSA）和离散对数（DH）难题都要难得多，以致于同样的安全强度下，椭圆曲线加密的密钥比RSA和DH的短不少，这是椭圆曲线加密的一大优势。

 

   有限域上的椭圆曲线:

   但是密码学中，并不能使用上面介绍的实数域上的椭圆曲线。因为

1. 实数域上的椭圆曲线是连续的，有无限个点，密码学要求有限点。

2. 实数域上的椭圆曲线的运算有误差，不精确。密码学要求精确。

所以我们需要引入有限域上的椭圆曲线。

 

所谓有限域上的椭圆曲线，简单来说就是满足下面式子要求的曲线（x, y, a, b都是小于素数p的非负整数）：

y2modp=x3+ax+bmodp其中4a3+27b2≠0modp

对比一下原先的椭圆曲线的方程：

y2=x3+ax+b其中4a3+27b2≠0

可以看到这个只是对原式进行了简单的取模处理而已。实际上RSA和DH中也是基于这种形式的取模运算，它们其实也都是在有限域上进行的。

 

一、         密码局限性（攻击方法）

椭圆曲线安全性依赖于基于椭圆曲线的有限群上的离散对数难题。于基于RSA的数字签名和基于有限域离散对数的数字签名相比，在相同的安全强度条件下，椭圆曲线方案有如下特点：签名长度短，密钥存储空间小，特别适用于存储空间有限、带宽受限、要求高速实现的场合（如在智能卡中应用）。

为使得有较好的安全性，这些参数的选取应满足如下条件：

(1)   P越大越安全，但越大，计算速度就越慢，160位可以满足目前的安全要求；

(2)   为了防止Pohlig-Hellman方法攻击，n为大于素数（n>）,对于固定的有限域GF(P)，n应当尽可能大；

(3)   因为+ax+b无重复因子才可基于椭圆曲线(a,b)定义群，所以要求4+27(mod p)；

(4)  为了防止小步——大步攻击，要保证P的阶n足够大，要求n4;

(5)   为了防止MOV规范法和Smart法，不能选取超奇异椭圆曲线和异常椭圆曲线等两类特殊的曲线。