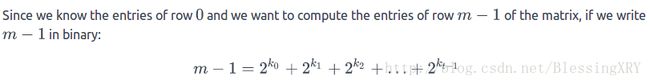【公式推导＋杨辉三角＋异或性质＋进制表示】XOR Matrix HackerRank - xor-matrix

Think:
1知识点：【公式推导＋杨辉三角＋异或性质＋进制表示】
2题意：
定义异或矩阵元素a[i, j]：

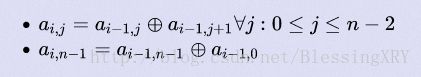
第一行输入n, m表示n行m列的异或矩阵，第二行输入n个元素表示异或矩阵的第一行，题目要求我们输出异或矩阵的第m行
2.1数据范围：
·1 <= n <= 1e5
·1 <= m <= 1e18
·1 <= a[i, j] <= 1e9
3解题过程
3.1公式推导：
a[i, j] = a[i-1, j] ^ a[i-1, j+1]
即对于a[i, j]单个元素：
a[0, j] = a[0, j]
a[1, j] = a[0, j] ^ a[0, j+1]
a[2, j] = a[1, j] ^ a[1, j+1] = (a[0, j] ^ a[0, j+1]) ^ (a[0, j+1] ^ a[0, j+2])
= a[0, j] ^ a[0, j+1] ^ a[0, j+1] ^ a[0, j+2]
a[3, j] = a[2, j] ^ a[2, j+1] = (······) ^ (······)
= a[0, j] ^ a[0, j+1] ^ a[0, j+1] ^ a[0, j+1] ^ a[0, j+2] ^ a[0, j+2] ^ a[0, j+2] ^ a[0, j+3]
   .
   .
   .
即：
a[i, j] ⇦ a[0, j]、a[0, j+1]、a[0, j+2]、···· 、a[0, j+i]
进而推得：
a[x+i, j] ⇦ a[x, j]、a[x, j+1]、a[x, j+2]、···· 、a[x, j+i]

3.2杨辉三角
将a[i, j]由a[0, j]、a[0, j+1]、a[0, j+2]、···· 、a[0, j+i]表示，发现系数满足杨辉三角：

3.3异或性质
·a[i, j] ^ a[i, j] = 0
·a[i, j] ^ 0 = a[i, j]
通过异或性质a[i, j] ^ a[i, j] = 0和a[i, j] ^ 0 = 0化简系数矩阵
得新的系数矩阵为：
0.           1
1.          1 1
2.         1 0 1
3.        1 1 1 1
4.       1 0 0 0 1
5.      1 1 0 0 1 1
6.     1 0 1 0 1 0 1
7.    1 1 1 1 1 1 1 1
8.   1 0 0 0 0 0 0 0 1
9.  1 1 0 0 0 0 0 0 1 1
…
即：
a[0, j] = a[0, j]
a[1, j] = a[0, j] + a[0, j+1]
a[2, j] = a[0, j] + a[0, j+2]
a[3, j] = a[0, j] + a[0, j+1] + a[0, j+2] + a[0, j+3]
a[4, j] = a[0, j] + a[0, j+4]
a[5, j] = a[0, j] + a[0, j+1] + a[0, j+4] + a[0, j+5]
a[6, j] = a[0, j] + a[0, j+2] + a[0, j+4] + a[0, j+6]
a[7, j] = a[0, j] + a[0, j+1] + a[0, j+2] + a[0, j+3] + a[0, j+4] + a[0, j+5] + a[0, j+6] + a[0, j+7]
a[8, j] = a[0, j] + a[0, j+8]
a[9, j] = a[0, j] + a[0, j+1] + a[0, j+8] + a[0, j+9]
可以发现，对于幂为2的行，只需要通过a[0, j]和a[0, j+i]两个二项式系数即可计算得到a[i, j]，即：

3.4进制表示：

4.【建议参考】题解代码：

#include 
using namespace std;

#define N 111111
int a[N];
int b[N];
int n;

void move(int k) {
    // compute the 2^k'th row
    for (int i = 0; i < n; i++) b[i] = a[i] ^ a[(i + (1LL << k)) % n];

    // copy back to 'a'
    for (int i = 0; i < n; i++) a[i] = b[i];
}
int main() {
    // take the input
    long long m;
    scanf("%d%lld", &n, &m);
    for (int i = 0; i < n; i++) scanf("%lld", &a[i]);

    // compute the answers
    m--;
    for (int k = 0; k < 60; k++) {
        if (m & (1LL << k)) move(k);
    }

    // print the answers
    for (int i = 0; i < n; i++) printf("%d ", a[i]);
}

vjudge题目链接

以下为Accepted代码

#include 

using namespace std;

typedef long long LL;
const int N = 104014;

int n, a[N], b[N];

void move(int k);

int main(){
  LL m;
  while(~scanf("%d %lld", &n, &m)){
    for(int i = 0; i < n; i++)
      scanf("%d", &a[i]);
    m--;
    for(int k = 0; k < 64; k++){
      if(m & (1LL << k)) move(k);
    }
    for(int i = 0; i < n; i++)
      printf("%d%c", a[i], i == n-1? '\n': ' ');
  }
  return 0;
}
void move(int k){
  for(int i = 0; i < n; i++)
    b[i] = a[i]^(a[(i+(1LL<for(int i = 0; i < n; i++)
    a[i] = b[i];
  return;
}