【平面图理论】平面图学习笔记
我为什么现在要学平面图
因为顺切HNOI2010遇到了平面图判定…
————————————–线割分是我>w<————————————————–
首先是一些定义:
什么是平面图?
对于一个图G=< V,E >,如果能把G画在一个平面上,且画出的图的任意两条边除了V中的节点没有其他交点,则图G为平面图.
平面图的面:
对于一个平面图,由如果存在一些边围成的区域,且这个区域内不包含这个图的点和边,那么我们称这个区域为该平面图的一个面.
比如这里面的红色区域:
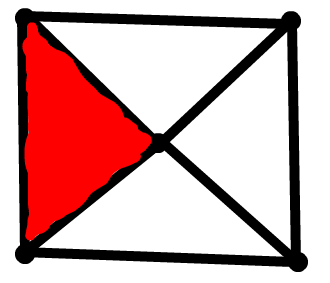
对于包围这个区域的那些边构成的圈,我们称之为这个面的边界.边界的长度,称为这个面的度.
我们定义一个面的集合F,于是对于平面图我们可以将其表示为G=< V,E,F >
平面图的性质(具体内容及证明见国家集训队2003论文刘才良《平面图在信息学中的应用》):
1.若图G=< V,E,F >为连通平面图, ∑f∈F d(f) =2|E|
2.若图G=< V,E,F >为连通平面图, |V|−|E|+|F|=2
当然,对于不连通的平面图,我们可以把它分解成几个联通块,然后对每个联通块这两个性质都成立(这是很显然的),所以就可以得到对不连通的平面图的一些性质.这里我不再赘述.
从上面两个性质又可以得到如下推论:
对于给定的连通简单平面图G=< V,E,F >,若|V|>=3,则|E|<=3|V|-6,|F|<=2|V|-4
原文的第二个推论我觉得好像有问题我不贴了,反正第二个好像也没用
第一个推论的作用就是告诉我们E的数量级是O(|V|)的…
平面图的判定(才不会说我就是因为这个才学平面图的):
做法转自这里
哈密顿回路会连成一个环,这个图必定被分成两部分,如果两条边相交无论同时在内还是在外都会相交,只有一条在环内一条在外才行——二分图!首先判断出那些边不再回路上然后把有矛盾的边连边利用染色法判断能否构成二分图,二分图的成立决定了平面图的成立。
接下来是重点:平面图与对偶图
定义:对于一个平面图,如果它有源点汇点,我们称之为s-t平面图.
每个平面图都能建出相应的对偶图.
对于一个平面图G,其对偶图为G*.G*中的一个点,对应原图G中的一个面.
对于G中的每条边e,如果e属于两个面 f1,f2 ,那么我们在G*中对点 f1∗,f2∗ 连一条边;
如果e只属于一个面f,那么在G*中对点 f∗,f∗ 连一条自环边.
此时有定理:
1.G的面数等于G*的点数,G与G*的边数相等.
2.对于一个s-t平面图,其对偶图中的一个环对应原图中的一个割.
此时就可以看出我们引入平面图与对偶图有什么作用了.
我们都知道求最大流的算法与最短路算法在效率上有不小的差距.
当我们看到一个题数据范围极大但是像是最大流,却又担心单纯的写最大流会TLE的时候
如果原图满足是平面图,我们不妨先转化为求最小割,然后再建出其对偶图然后求解.
对对偶图跑一遍Heap-Dijkstra,利用它求出的距离来做距离标号,构造最大流.
具体题目我好像只知道BeiJing2006 狼与兔子QAQ
之后单独写题解