Transformer小结
Attention is all you need
Transformer
LayerNorm(x + Sublayer(x))
整理的Transformer 伪代码
输入 Inputs 输出 Outputs
X = Positional_Encoding(Input_Embedding(Inputs))
X = LayerNorm(X + Multi-Head_Attention(X))
X = LayerNorm(X + Feed_Forward(X))
Y = Positional_Encoding(Output_Embedding(Outputs))
Y = LayerNorm(Y + Masked_Multi-Head_Attention(Y))
Y = LayerNorm(Y + Multi-Head_Attention( X Q X_Q XQ, X K X_K XK, Y V Y_V YV))
Y = LayerNorm(Y + Feed_Forward(Y))
Y = Linear(Y)
Output Probabilities = Softmax(Y)
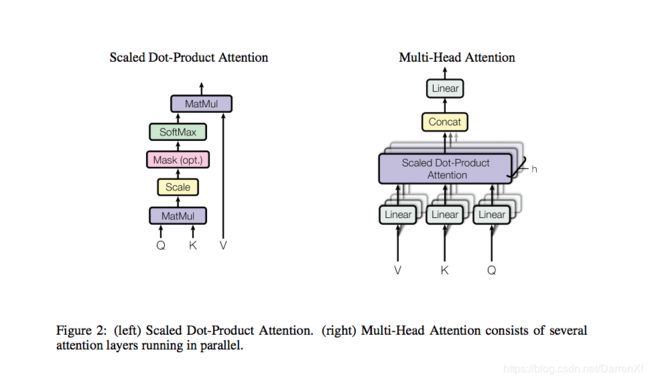
Scaled Dot-Product Attention
Attention(Q, K, V) = softmax( Q K T d k \frac{QK^T}{\sqrt{d_k}} dkQKT)V
Multi-Head Attention
MultiHead(Q,K,V) = Concat( h e a d 1 head_1 head1,…, h e a d h head_h headh) W O W^O WO
where h e a d i head_i headi = Attention( Q W i Q QW_i^Q QWiQ, K W i K KW_i^K KWiK, V W i V VW_i^V VWiV)
W i Q ∈ R d m o d e l ∗ d k W_i^Q ∈ R^{d_{model} \quad * \quad d_k} WiQ∈Rdmodel∗dk
W i K ∈ R d m o d e l ∗ d k W_i^K ∈ R^{d_{model} \quad * \quad d_k} WiK∈Rdmodel∗dk
W i V ∈ R d m o d e l ∗ d v W_i^V ∈ R^{d_{model} \quad * \quad d_v} WiV∈Rdmodel∗dv
W i O ∈ R h d v ∗ d m o d e l W_i^O ∈ R^{hd_v \quad * \quad d_{model}} WiO∈Rhdv∗dmodel
In this work we employ h = 8 parallel attention layers, or heads.
For each of these we use d k d_k dk = d v d_v dv = d m o d e l d_{model} dmodel/h = 64
Due to the reduced dimention of each head, the total computational cost
is similar to that of single-head attention with full dimensionality.
Position-wise Feead-Forward Networks
FFN(x) = max(0, x W 1 xW_1 xW1 + b 1 b_1 b1) W 2 W_2 W2 + b 2 b_2 b2
Positional Encoding
$PE_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}}) $
$PE_{(pos, 2i+1)} = cos(pos/10000^{2i/d_{model}}) $
where pos is the position and i is the dimension.
重新写Transformer的伪代码
输入 Inputs 输出 Outputs
X = Positional_Encoding(Input_Embedding(Inputs))
Q X Q_X QX, K X K_X KX, V X V_X VX = X
X = LayerNorm(X + Multi-Head_Attention( Q X Q_X QX, K X K_X KX, V X V_X VX))
X = LayerNorm(X + Feed_Forward(X))
Q X Q_X QX, K X K_X KX, V X V_X VX = X
Y = Positional_Encoding(Output_Embedding(Outputs))
Q Y Q_Y QY, K Y K_Y KY, V Y V_Y VY = Y
Y = LayerNorm(Y + Masked_Multi-Head_Attention( Q Y Q_Y QY, K Y K_Y KY, V Y V_Y VY))
Q Y Q_Y QY, K Y K_Y KY, V Y V_Y VY = Y
Y = LayerNorm(Y + Multi-Head_Attention( Q X Q_X QX, K X K_X KX, V Y V_Y VY))
Y = LayerNorm(Y + Feed_Forward(Y))
Y = Linear(Y)
Output Probabilities = Softmax(Y)
Hardware and Schedule
We trained our models on one machine with 8 NVIDIA P100 GPUs.
We trained the base models for a total of 100,000 steps or 12 hours.
The big models were trained for 300,000 steps(3.5days)
Optimizer
We used the Adam optimizer with with β 1 β_1 β1 = 0.9, β 2 β_2 β2 = 0.98 and ϵ \epsilon ϵ= 10^{−9}$
Regularization
Residual Dropout
Label Smoothing