CTR预估 论文精读(三)--Factorization Machines

Abstract

In this paper, we introduce Factorization Machines (FM) which are a new model class that combines the advantages of Support Vector Machines (SVM) with factorization models. Like SVMs, FMs are a general predictor working with any real valued feature vector. In contrast to SVMs, FMs model all interactions between variables using factorized parameters. Thus they are able to estimate interactions even in problems with huge sparsity (like recommender systems) where SVMs fail. We show that the model equation of FMs can be calculated in linear time and thus FMs can be optimized directly. So unlike nonlinear SVMs, a transformation in the dual form is not necessary and the model parameters can be estimated directly without the need of any support vector in the solution. We show the relationship to SVMs and the advantages of FMs for parameter estimation in sparse settings.

On the other hand there are many different factorization models like matrix factorization, parallel factor analysis or specialized models like SVD++, PITF or FPMC. The drawback of these models is that they are not applicable for general prediction tasks but work only with special input data. Furthermore their model equations and optimization algorithms are derived individually for each task. We show that FMs can mimic these models just by specifying the input data (i.e. the feature vectors). This makes FMs easily applicable even for users without expert knowledge in factorization models.

1. FM vs SVM

1.1 SVM 缺陷：

1. 支持向量机是机器学习和数据挖掘中最常用的预测模型之一。然而, 在协同过滤等设置中, 支持向量机没有发挥重要作用, 最好的模型要么是标准矩阵/张量分解模型的直接应用, 如 PARAFAC[1], 要么是使用分解参数的特定模型 [2], [3], [4].

   本文表明, 标准支持向量机预测器在这些任务中不成功的唯一原因是, 它们在非常稀疏的数据下, 无法在复杂 (非线性) 内核空间中学习到可靠的参数 (“超平面”)。

1.2 Tensor factorization model缺陷

另一方面, 张量分解模型，甚至是特定的因子分解模型的通病则是：

• 不适用于标准预测数据 (例如 $R^n$ 中的实值特征向量) ；
• 特定模型通常是为特定任务单独推导出来的, 需要花费大量精力进行建模与学习算法设计。

1.3 Factorization Machine

Factorization Machine(FM) 是一个如SVM一般的通用预测器，但是却能在非常稀少的情况下学习到可靠参数。

因子分解机对所有嵌套变量的交互(nested variable interactions)进行建模 (可与支持向量机中的多项式内核相比较)，但使用分解参数化(factorized parametrization)，而不是像 svm 中那样密集的参数化。

1.4 FM, SVM 以及collaborative filter对比

FM:

• 结果表明, FM 的模型等式可以在线性时间内完成计算, 并且它只取决于线性数量的参数。
• 这样就可以直接优化和存储模型参数, 而不需要存储任何训练数据 (例如支持向量) 进行预测。

non-linear SVM

• 非线性支持向量机通常依赖部分训练数据 (支持向量)以双重形式（对偶计算）进行优化和计算预测 (模型方程)。

collaborative filter

结果表明，FM超过了很多对于协同过滤任务的成功算法，如带偏置的FM，SVD++，PITF以及FPMC。

1.5 FM优势

1. FM 允许在非常稀疏的数据下进行参数估计，而SVM则不能；
2. FM具有线型复杂度，可以在原始数据上进行优化，而无需依赖如SVM一般的支持向量；（论文展示了 FM 可扩展到具有1亿个训练实例的大型数据集 (如 Netflix)。）
3. FM 是一个通用的预测器, 可以使用任何为真实值的特征矢量。而其他因子分解模型模型仅在非常受限的输入数据上工作。（论文展示, 只要定义输入数据的特征向量, FM 就可以拟合最新的模型, 如biased MF、SVD ++、PITF 或 FPMC。）

2. 多项式模型

2.1 多项式模型形式

考虑一个模型，它的输出由单特征（$d$ 维）与组合特征的线性组合构成，如果不看二次项，这就是一个线性回归模型，现在引入了交叉项。
$$y(\mathbf{x})=w_0+\sum _{i=1}^n{w}_i\cdot x_i+\sum _{i=1}^n\sum _{j=i+1}^n{w}_{ij}\cdot x_i{x}_j$$
其中单特征的参数 $w_i$ 有 $d$ 个，组合特征的参数 $w_{ij}$ 有 $\frac{d(d-1)}{2}$ 个，且任意两个 $w_{ij}$ 之间相互独立。

2.2 交叉项参数训练问题

现在假设目标函数是 $L(y,f(x))$，为了使用梯度下降法训练交叉项参数，需要求导：
$$\frac{\partial L}{\partial w_{ij}}=\frac{\partial L}{\partial f(x)}\cdot \frac{\partial f(x)}{\partial w_{ij}}=\frac{\partial L}{\partial f(x)}{x}_i{x}_j$$

也就是说，每个二次项参数 $w_{ij}$ 的训练需要 $x_i$ 和 $x_j$ 同时非零，若特征稀疏（例如Onehot过），则一整行中只有一个1，容易导致 $w_{ij}$ 训练无法进行。

3. FM

3.1 FM模型

将矩阵 $W=w_{i,j}$ 矩阵（这是一个对称方阵）分解成 $W=V^{T}V$ 的形式，其中 $V=(v_1,v_2,\cdots ,v_d)$ 是一个 $k\times d$ 矩阵，且 $k\ll d$，于是 $W$ 矩阵的每一个元素都可以用 $V$ 矩阵对应的两列做内积得到：$w_{ij}=v_i\cdot v_j$，同时多项式模型可以重写，这就是因子分解机模型。

$$y(\mathbf{x})=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^n\sum _{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j$$

由于只需要用分解后产生的 $V$ 就能表达 $W$，使得参数个数由 $d^2$ 变成了 $kd$。另一方面，$V$ 矩阵的每一列 $v_i$ 是第 $i$ 维特征的隐向量，一个隐向量包含 $k$ 个描述第 $i$ 维特征的因子，故称因子分解。

3.2 FM能解决参数训练问题的原因

经过因子化之后，组合特征 $x_i{x}_j$ 和 $x_j{x}_k$ 的系数 $(v_i\cdot v_j)$ 与 $(v_j\cdot v_k)$ 不再独立，他们共有了 $v_j$，因此所有包含 $x_j$ 特征的非零组合特征的样本都能拿来训练。这是什么意思呢？现在，如果只看交叉项（不管用什么loss，根据链式法则我们总需要乘上 $\frac{\partial f(x)}{\partial w_{ij}}$：

$$f(x)\propto \sum _i\sum _j{w}_{ij}{x}_i{x}_j\to \frac{\partial f(x)}{\partial w_{ij}}=x_i{x}_j$$
对于稀疏数据而言，$x_i{x}_j=0$ 很常见，梯度为0，FM改一下变成：
$$f(x)\propto \sum _i^d\sum _{j=i+1}^d(v_i\cdot v_j)x_i{x}_j\to \frac{\partial y}{\partial v_i}=\sum _j{v}_j\cdot x_i{x}_j$$

原本的多项式模型，为了训练 $w_{ij}$，要求 $x_i$ 和 $x_j$ 不能同时为0，现在我们假设 $x_i̸=0$，则条件变为 “$x_j$ 绝对不可以为0”。另一方面，同样假设 $x_i̸=0$，但是对 $j$ 没有限制，在所有的特征中，任意不为0的 $x_j$ 都可以参与训练，条件减弱为 “存在 $x_j̸=0$ 即可”。因此，FM缓解了交叉项参数难以训练的问题。

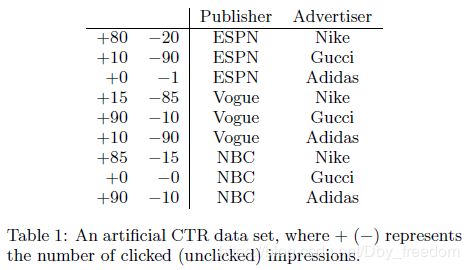
论文 Filed-aware Factorization Machines for CTR Prediction 中，例举了两个很好的示例显示出FM与多项式模型的差别。

For Poly2, a very negative weight $w_{ESPN,Adidas}$ might be learned for this pair. For FMs, because the prediction of (ESPN, Adidas) is determined by $w_{ESPN}\cdot w_{Adidas}$, and because $W_{EPSN}$ and $w_{Adidas}$ are also learned from other pairs (e.g., (ESPN, Nike), (NBC, Adidas)), the prediction may be more accurate.
Another example is that there is no training data for the pair (NBC, Gucci). For Poly2, the prediction on this pair is trivial, but for FMs, because wNBC and wGucci can be learned from other pairs, it is still possible to do meaningful prediction.
注：这里的Ploy2的联结特征处理方式与多项式模型相同，都是需要联立特征同时非零才能得到准确训练值（而大规模稀疏条件下，同时非零对可能不存在或者很少）；

总结：
而FM的提升点主要就是将 $w_{i,j}$ 转换为 $<v_i,v_j>$ 来计算，其中 $v_i,v_j$ 是一个 $k\ast 1$的矩阵，整个 $V=(v_1,v_2,\cdots ,v_d)$ 是一个 $k\times d$ 矩阵，即使不存在特征 $i,j$ 同时非零的样本，依旧可以凭借其他包含组合项计算得到 $v_i,v_j$， 如组合项存在非零值的 $<v_i,v_a>$, $<v_c,v_j>$等。这才是FM对于稀疏特征处理的最大优势所在，当然，相比于多项式模型，速度提升是第二大优势。

3.3 FM计算的复杂度

$$f(x)\propto \sum _i^d\sum _{j=i+1}^d(v_i\cdot v_j)x_i{x}_j$$
时间复杂度上，若只看交叉项，两层循环 $O(n^2)$，内层k维内积$(O(k))$，综合起来应该是 $O(k{d}^2)$。然而，交叉项是可以化简的，化简为下面的形式后，复杂度是 $O(kd)$。
$$\sum _{i=1}^n\sum _{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j=\frac{1}{2}\sum _{f=1}^k\left({\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)}^2-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2\right)$$
其推导过程如下：
$$\begin{gathered} \sum _{i=1}^n\sum _{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j(1) \\ =\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j-\frac{1}{2}\sum _{i=1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_i⟩x_i{x}_i(2) \\ =\frac{1}{2}\left(\sum _{i=1}^n\sum _{j=1}^n\sum _{f=1}^k{v}_{i,f}{v}_{j,f}{x}_i{x}_j-\sum _{i=1}^n\sum _{f=1}^k{v}_{i,f}{v}_{i,f}{x}_i{x}_i\right)(3) \\ =\frac{1}{2}\sum _{f=1}^k⟮\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)\cdot \left(\sum _{j=1}^n{v}_{j,f}{x}_j\right)-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2⟯(4) \\ =\frac{1}{2}\sum _{f=1}^k⟮{\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)}^2-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2⟯ \end{gathered}$$

CSDN貌似不支持多行公式编辑，没办法，舍弃了样式，同志们将就着看。

3.4 FM的梯度下降求解

FM模型方程似乎是通用的，根据任务不同，使用不同的loss。比如，回归问题用MSE，分类问题先取sigmoid或者softmax，然后用cross-entropy，比较灵活。
$$f(x)=w_0+\sum _{i=1}^n{w}_i\cdot x_i+\frac{1}{2}\sum _{f=1}^k\left({\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)}^2-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2\right)$$
我们再来看一下FM的训练复杂度，利用SGD（Stochastic Gradient Descent）训练模型。模型各个参数的梯度如下：
$$\frac{\partial }{\partial \theta }y(\mathbf{x})=\{\begin{array}{ll}1,& \text{if}\theta \text{is}{w}_0\\ x_i,& \text{if}\theta \text{is}{w}_i\\ x_i{\sum }_{j=1}^n{v}_{j,f}{x}_j-v_{i,f}{x}_i^2,& \text{if}\theta \text{is}{v}_{i,f}\end{array}$$
其中，$v_{j,f}$ 是隐向量 $v_j$ 的第 $f$ 个元素。由于 ${\sum }_{j=1}^n{v}_{j,f}{x}_j$ 只与 $f$ 有关，而与 $i$ 无关，在每次迭代过程中，只需计算一次所有 $f$ 的 ${\sum }_{j=1}^n{v}_{j,f}{x}_j$ 就能够方便地得到所有 $v_{i,f}$ 的梯度。显然，计算所有 $f$的 ${\sum }_{j=1}^n{v}_{j,f}{x}_j$ 的复杂度是 $O(kn)$；已知 ${\sum }_{j=1}^n{v}_{j,f}{x}_j$ 时，计算每个参数梯度的复杂度是 $O(1)$；得到梯度后，更新每个参数的复杂度是 $O(1)$ 模型参数一共有 $nk+n+1$ 个。因此，FM参数训练的复杂度也是 $O(kn)$。综上可知，FM可以在线性时间训练和预测，是一种非常高效的模型。

4. FM vs SVM

4.1 Linear kernel SVM Model

线性核：
$$K_l(x,z):=1+<x,z>$$
线性SVM模型等式可写为：
$$\hat{y}=w_0+\sum _{i=1}^n{w}_i{x}_i{w}_0\in R,w\in R^n$$
线性SVM相当于 $d=1$ 的FM情况。

4.2 Polynomial kernel

多项式核允许SVM对变量之间高阶交叉项进行建模，被定义为：
$$\begin{gathered} \varphi (x):=(1,\sqrt{2}{x}_1,\dots ,\sqrt{2}{x}_n,x_1^2,\dots ,x_n^2, \\ \sqrt{2}{x}_1{x}_2,\dots ,\sqrt{2}{x}_1{x}_n,\sqrt{2}{x}_2{x}_3,\dots ,\sqrt{2}{x}_{n-1}{x}_n) \end{gathered}$$
因此多项式核的SVM可表示为：
$$\hat{y}=w_0+\sqrt{2}\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^n{w}_{i,j}^{(2)}{x}_i^2+\sqrt{2}\sum _{i=1}^n\sum _{j=i+1}^n{w}_{i,j}^{(2)}{x}_i{x}_j$$
其中$w_0\in R,w\in R^n,W^{(2)}\in R^{n\times n}$ (symmetric matrix)

4.3 多项式核SVM与FM的区别

多项式核SVM与FM的区别在于，多项式核SVM中的$w_{i,j}$是完全独立的，如 $w_{i,j}$ 和 $w_{i,l}$ ，而FM的$w_{ij}$ 被因子分解，因此 $<v_i,v_j>$ 与 $<v_i,v_l>$ 彼此依赖，因为他们重叠并且共享参数 $v_i$。

这也是为什么多项式核SVM为什么在高稀疏环境下不能学习到交叉项模型稀疏的原因，因为$w_{ij}$ 与 $w_{i,l}$ 彼此独立，若想进行参数 $w_{ij}$ 的学习，必须保证特性 $i$ 项与特征 $j$ 项同时不为0，这在协同过滤以及高稀疏环境下是难以保证的，更多时候两者甚至永远不能同时非零；

相比之下，FM的巧妙之处就是将 $w_{ij}$ 进行了因子分解，其$w_{ij}$ 可以被分解为结构$<v_i,v_j>$ ，而$v_i,v_j$ 相对于$w_{ij}$ 要容易训练的多，具体原因参考上文3.2 FM能解决参数训练问题的原因。

4.4 稀疏环境下的参数估计

这里作者以只有用户 user 以及 item 两个特征属性进行举例说明：

1) 线性核SVM：
$$\hat{y}=w_0+w_u+w_i$$
只有 $j=u$ 或者 $j=i$时，$w_j=1$

事实证明，线性核SVM可以在很稀疏的样本中进行训练，但是表现非常差，如上图2.

2） 多项式核SVM

对于只有两特征user与item，$m(x)=2$，则多项式核SVM如下：
$$\hat{y}=w_0+\sqrt{2}(w_u+w_i)+w_{u,u}^{(2)}+w_{i,i}^{(2)}+\sqrt{2}{w}_{u,i}^{(2)}$$
其中 $w_u$ 与 $w_{u,u}^{(2)}$ 表示含义相同，可以去掉一个，$w_i$ 与 $w_{i,i}^{(2)}$同理可去掉一个，此时只是相比线性核多了一个交叉项$w_{u,i}^{(2)}$，而若想要有效评估参数 $w_{u,i}^{(2)}$，必须有足够多满足 $x_i̸=0\wedge x_j̸=0$ 的交叉项，因为一旦其中之一为0，则该对应样本就无法用于评估$w_{i,j}^{(2)}$。

4.5 总结

1. svm 的密集参数需要同时存在的非零项对，这在稀疏样本中是难以实现的；而FM则可以在稀疏样本下很好地评估交叉项参数；（具体原因看3.2小节及4.4小节）

2. FM 可以直接以原始形式学习，而非线性SVM往往要借助对偶形式进行不等式优化求解；

3. FM独立与训练数据，而SVM则依赖部分数据（支持向量机）。

5. FM vs Other Factorization Models

FM在使用正确输入的情况下，可以拟合任何其他因子分解模型。

1. 像 PARAFAC 或 MF 这样的标准分解模型不如FM这般通用，这些标准分解模型需要特征被分为 m 块，每块只有一个1，其余元素为0（one-hot编码）

2. 对于单个任务设计的特性分解模型，作者证明FM通过特征提取，可以拟合任何分解模型（包括MF, PARAFAC, SVD++, PITF, FPMC），这也使得FM可以在现实中更通用。

6. 结论

FM 将 SVM 的通用性与分解模型的优点结合起来；

与SVM对比：

• FM能够在稀疏严重的情况下估计参数；
• 模型等式只依赖模型参数（SVM还需依赖部分数据——支持向量）
• 可以在原始形式下直接优化（对于SVM的对偶处理方式）

FM的拟合能力不弱于任何多项式核SVM。

与分解模型对比：

• FM是一个通用预测器，可以处理任何真实值向量；（对比分解模型往往只在特定输入数据形式下才能工作）
• 只需在输入特征向量中使用正确的指示（即某些特定组合方式），FM可以近似于任何为单任务设计的特性最新模型，这些模型包括MF, SVD++和FPMC。