matlab中的图像坐标系统

有时我们的图显示了没有轴标记的图像。这是函数imshow的默认行为。但是几何图像变换的分析和解释是通过显示这些形象的排列来辅助的。开启标记的一种方法是在调用imshow之后调用axis。例如：

f=imread('circuit-board.tif');
imshow(f)
axis on
xlabel x
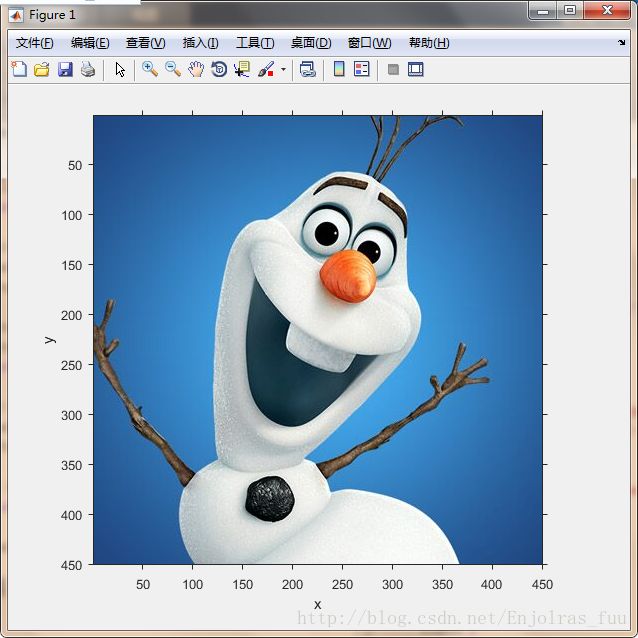
ylabel y

如图，原点在左上角，x轴是水平的，并且向右延伸；y是垂直的，并且向下延伸。这个约定即图像空间坐标系统。在这个系统中，x轴和y轴与规定的图像坐标系统相反。用于设置一定的用户参数选择的工具箱函数iptsetpref可用于始终产生imshow以显示记号标志。为转向带有记号和标记的显示，可调用

iptsetpref imshowAxesVisible on

对于包含M行、N列的图像来说，默认的XData向量是[1,N],默认的YData向量是[1,M
]。可以设置XData和YData特性为其他的值，当工作在几何变换时，这可能非常有用。imshow函数通过可选择的参数值对的使用来支持这一功能。例如，用下面的语法来显示图像，左边和右边像素的中心在x轴的-20和20处，顶部和底部的像素在y轴的-10和10处：

imshow(f,'XData',[-20,20],'YData',[-10,10])
axis on
xlabel x
ylabel y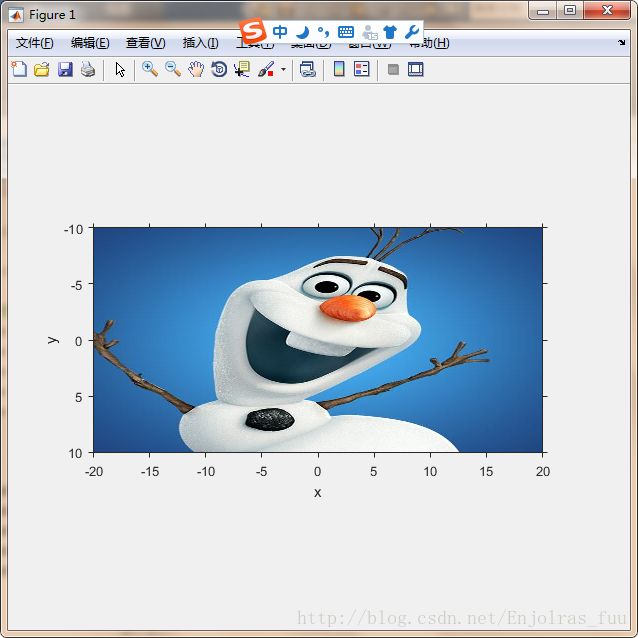

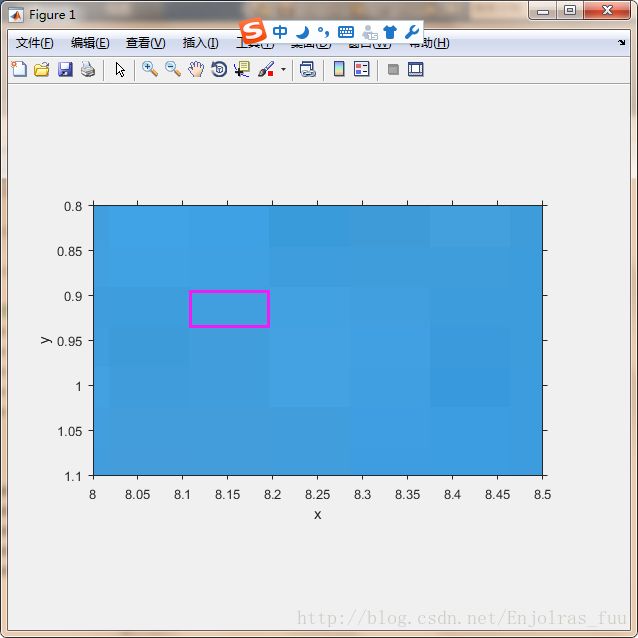
用以下命令放大图像左上角之后的结果：发现其中的像素已经不再是正方形。

axis([8 8.5 0.8 1.1])

关于输出图像位置前面我们谈论了一副用仿射变换旋转过的图像。然而注意，那幅图像并没有显示输出图像的位置。函数imtransform可以通过使用附加参数来提供这个信息。调用语法是：

[g,xdata,ydata]=imtransform(f,tform)

当使用imshow显示图像时，第2个和第3个参数可以像XData和YData参数那样来使用。下面的例子说明了如何使用这些输出参量在相同的坐标系统中一起显示输入和输出图像。

在这个例子中，我们使用旋转和平移来研究如何在相同的坐标系中与输入图像一起显示和定位输出图像。我们以使用标以记号的轴和标记显示原始图像开始。

imshow(f)
axis on

下面我们用imtransform使图像旋转3*pi/4弧度

theta=3*pi/4;
T=[cos(theta) sin(theta) 0
   -sin(theta) cos(theta) 0
   0           0          1];
tform=maketform('affine',T);
[g,xdata,ydata]=imtransform(f,tform,'FillValue',255);

我们在前边一行代码调用imtransform来说明两个新的概念。第一个是可选择的输出参量xdata和ydata的使用，这些用于在xy坐标系统中定位输出图像。另一个概念是选择输入参量：’FillValue’,255。FillValue参数指定用于任何输出图像像素的值，对应输入图像边界外的输入空间位置。
在默认的情况下，FillValue参数的值是0，即黑色。在这个例子中，我们希望它们是白色的。下边，我们希望遵循matlab的常用模式：
（1）创建第一个绘图或者图像显示。
（2）调用hold on，以便后续的绘图或显示命令不清除该图。
（3）创建第二个绘图或者是绘图显示。
当显示输出图像时，从imtransform可选择的输出一起使用imshow的XData/YData语法：

imshow(f)
hold on
imshow(g,'XData',xdata,'YData',ydata)

接下来使用axis函数自动扩展轴的限制，以便两幅图像同时可见：

axis auto

最后，打开标有记号的轴和标记：

axis on

在结果中可以看到，仿射变换关于系统坐标原点（0,0）旋转图像。

接下来，我们检验平移，这是比旋转简单的仿射变换。但是，在目测时有可能被搞混。我们以构成仿射变换tform结构开始，向右移动500，向下移动200：

T=[1 0 0;0 1 0;500 200 1];
tform=maketform('affine',T);

接下来，我们使用基本的imtransform语法显示结果：

g=imtransform(f,tform);
imshow(g)
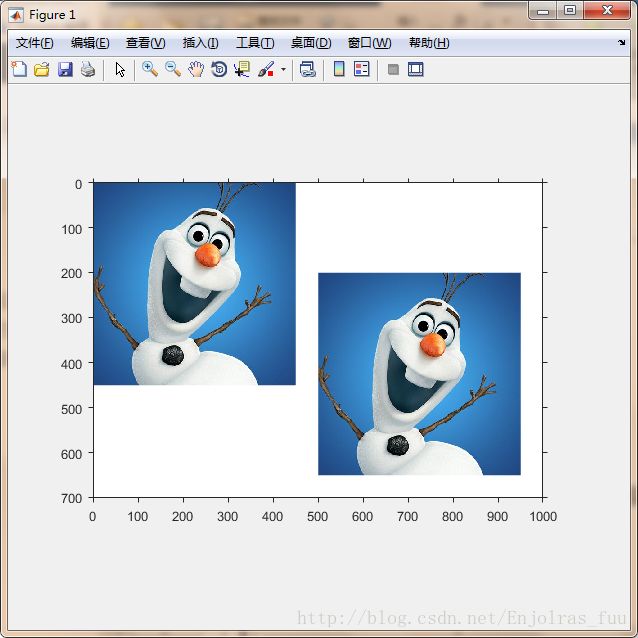
axis on

显示的结果很像原始图像，原因是imtransform正好自动地在输出空间上获取足够的像素以显示变换后的图像。这个自动行为消除了平移。为了看清平移效果，我们使用与上边旋转相同的技术：

[g,xdata,ydata]=imtransform(f,tform,'FillValue',255);
imshow(f);
hold on;
imshow(g,'XData',xdata,'YData',ydata)
axis on
axis auto

关于输出控制网格：
上面说明了如何用xdata和ydata参数形象化平移的效果，从输出imtransform到输入imshow。另一个说法是在输出空间中用imtransform直接控制像素网格。通常，imtransform在输出空间中用下列步骤定位和计算输出图像。
（1）决定输入图像的边界矩阵；
（2）在边界矩阵上把点变换到输出空间中；
（3）计算变换后输出空间中点的边界矩阵；
（4）计算位于输出空间中、边界矩形内的网格上的输出图像像素。
如下自定义函数说明了xdata和ydata参数的使用。这是imtransform的另一个变异，总使用像输出空间矩阵那样的输入空间矩阵。这样一来，输入和输出图像的位置便可以更直接进行比较：

function g=imtransform2(f,varargin)
% IMTRANSFORM2 2-D image transformation with fixed output location
% G=IMTRANSFORM2(F,TFORM,...)applies a 2-D geometric
% transformation to an image.IMTRANSFORM2 fixes the output image
% location to cover the same region as the input image.
% IMTRANSFORM2 takes the same set of optional parameter/value
% pairs as IMTRANSFORM.
[M,N]=size(f);
xdata=[1 N];
ydata=[1 M];
g=imtransform(f,varargin{:},'XData',xdata,'YData',ydata);

函数imtransform2是封装函数的典型示例。封装函数接受输入，有可能改进它们或把它们相加，然后把它们传递给另一个函数。书写封装函数的一种简单方法创建现有函数的变量，这个函数有不同的默认行为，可以容易地使用varargin是书写封装函数的特点。
在下面这个例子中，我们针对几个几何变换，比较imtransform和imtransform2的输出：

f=imread('lena.png');
imshow(f)

这样就显示了原始图像，我们的第一个变换是平移：

tform1=maketform('affine',[1 0 0;0 1 0;300 500 1]);
g1=imtransform2(f,tform1,'FillValue',200);
h1=imtransform(f,tform1,'FillValue',200);
imshow(g1),figure,imshow(h1)

我们的第二个变换在两个方向上用因子4收缩输入图像：

tform2=maketform('affine',[0.25 0 0;0 0.25 0;0 0 1]);
g2=imtransform2(f,tform2,'FillValues',200);
h2=imtransform(f,tform2,'FillValues',200);
imshow(g2),figure,imshow(h2)

此时，两个输出显示了全部输出图像。从imtransform2的输出可以看到，虽然比变换后的图像大，但填充的像素灰度很协调。来自函数imtransform的输出刚好包含变换后的图像。