numpy 矩阵运算

Python 矩阵运算

1、Python numpy 向量运算库

numpy 通过matrix基类支持向量运算， 下面是生产向量的方法

代码&执行结果：
虽然array与matrix形式上类似， 但不是一回事哦；我们可以通过array生成matrix对象， matrix对象提供矩阵计算功能。

>>> from numpy import *;
>>> #numpy 多维数据组件， 不支持向量运用
>>> a1=array([1,2,3]);
>>> type(a1)
'numpy.ndarray'>
>>> #numpy 矩阵组件， 支持向量运算
>>> a1=mat(a1);
>>> type(a1)
'numpy.matrixlib.defmatrix.matrix'>
>>> a1
matrix([[1, 2, 3]])
>>> 

2、矩阵加法

2.1、矩阵与标量相加

矩阵与标量相加， 相当于矩阵的每个元素都加上同一个标量。

>>> a = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> a = mat(a)
>>> a
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
>>> # 矩阵a与标量常数1相加
>>> a + 1
matrix([[ 2,  3,  4],
        [ 5,  6,  7],
        [ 8,  9, 10]])
>>> 

2.2、矩阵与向量相加

结果显示为矩阵中的每个向量都加上相同的向量。

>>> a = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> b = array([10, 20, 30])
>>> a = mat(a)
>>> b = mat(b)
>>> a
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
>>> b
matrix([[10, 20, 30]])
>>> a+b
matrix([[11, 22, 33],
        [14, 25, 36],
        [17, 28, 39]])

2.2、矩阵与矩阵相加

矩阵中的各个向量各种相关

>>> a
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
>>> a + a
matrix([[ 2,  4,  6],
        [ 8, 10, 12],
        [14, 16, 18]])
>>> 

3、 矩阵乘法

3.1 矩阵与标量相乘

矩阵每个元素乘与相同标量， 跟加法有点类似

>>> a
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
>>> a*2
matrix([[ 2,  4,  6],
        [ 8, 10, 12],
        [14, 16, 18]])

3.2 矩阵与向量相乘

矩阵乘法是矩阵运算中最重要的操作之一。两个矩阵A 和B 的矩阵乘积
（matrix product）是第三个矩阵C。为了使乘法定义良好，矩阵A 的列数必须和矩阵B 的行数相等。如果矩阵A 的形状是m x n，矩阵B 的形状是n x p，那么矩阵C 的形状是mxp。我们可以通过将两个或多个矩阵并列放置以书写矩阵乘法，例如C = A*B; 需要注意的是，两个矩阵的标准乘积不是指两个矩阵中对应元素的乘积。具体地，该乘法操作定义为:

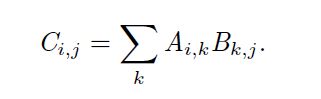
从公式来看矩阵乘法的规则定义相当奇怪， 难以理解， 矩阵的本质就是线性方程式，两者是一 一对应关系。如果从线性方程式的角度，理解矩阵乘法就毫无难度， 可参考博客《理解矩阵乘法》

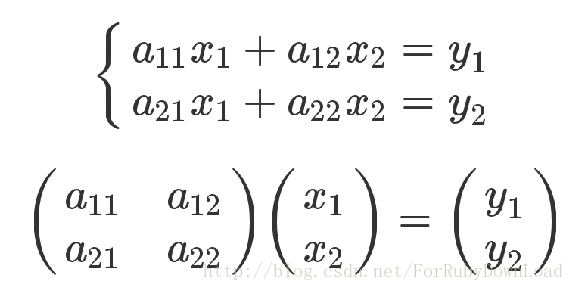
Numpy 矩阵运算代码：

>>> A
matrix([[1, 2],
        [2, 3],
        [3, 4]])
>>> B
matrix([[1, 2, 3, 5],
        [2, 3, 4, 6]])
>>> C = A*B
>>> C
matrix([[ 5,  8, 11, 17],
        [ 8, 13, 18, 28],
        [11, 18, 25, 39]])