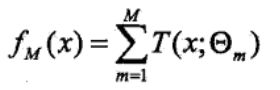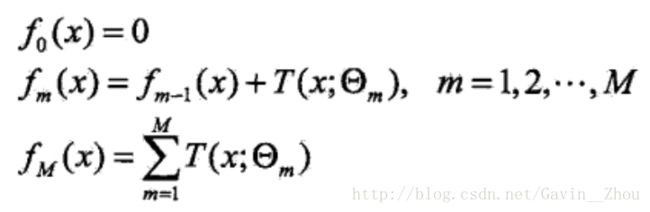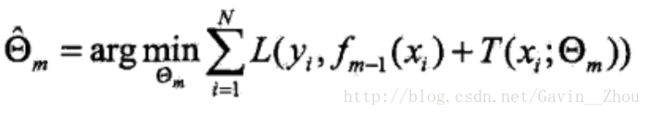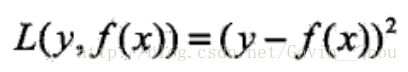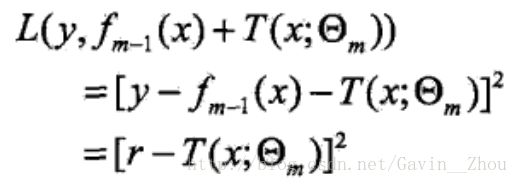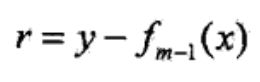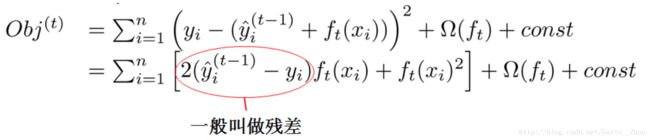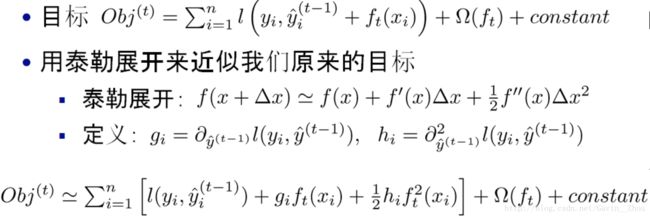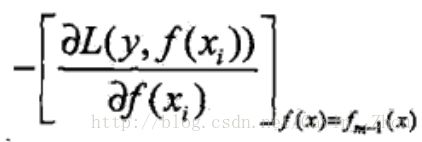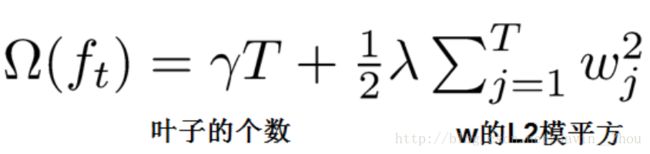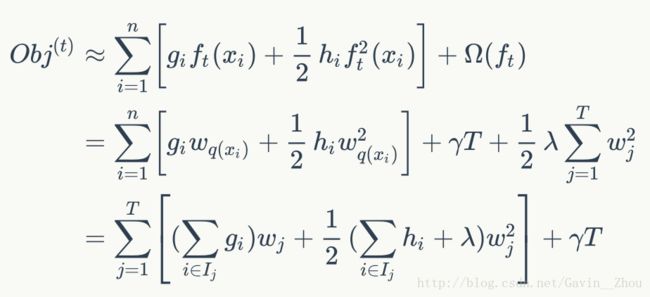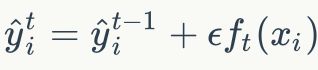GBDT(Gradient Boosting Decision Tree)

GBDT+FFM(FM)+Online Learing(FTRL)是kaggle比赛的重点方法，而且暑期实习面试的时候也有很多面试官问了，还是很有必要学习下的. 我在网上找了下相关资料，感觉讲的都不是很好(可能是我太菜了吧)，所以自己想着写一篇，要是哪里错了，欢迎指正

---

从Ensemble说起

Bagging，Boosting和Stacking是集成学习的三种主要的形式.

Bagging

Bagging=Bootstrap Aggregating，是model averaging的策略.
bootstrap是一种有放回的抽样，那么bagging就是使用bootstrap抽样来进行模型平均(vote). 从训练集从进行子抽样组成每个基模型所需要的子训练集，对所有基模型预测的结果进行综合产生最终的预测结果.

比如: Random Forest就是使用bagging的思想
(1) bootstrap抽样产生样本集M
(2) 从原始的K个特征中选择k(logK)个随机特征作为特征集F
(3) 对样本集M在特征集F上建立决策树(CART)
(4) 重复(1)-(3)产生多个决策树
(5) 投票(average)

这里借鉴别人的一张图：

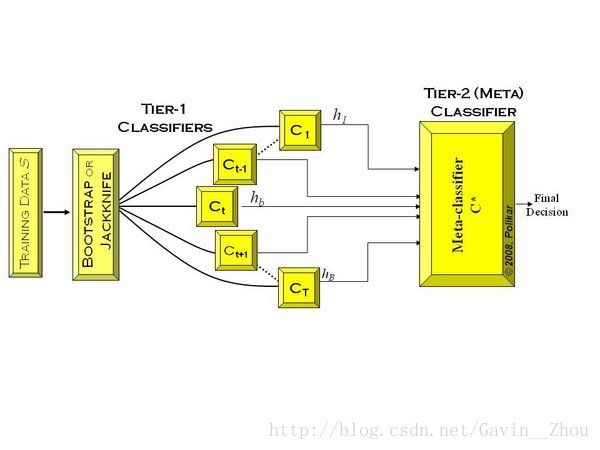
Stacking

是指训练一个模型用于组合其他各个模型。即首先我们先训练多个不同的模型，然后再以之前训练的各个模型的输出为输入来训练一个模型，以得到一个最终的输出.
将训练好的所有基模型对训练基进行预测，第j个基模型对第i个训练样本的预测值将作为新的训练集中第i个样本的第j个特征值，最后基于新的训练集进行训练。同理，预测的过程也要先经过所有基模型的预测形成新的测试集，最后再对测试集进行预测.

别人的一个图画的很好，这里拿来：

Boosting

While boosting is not algorithmically constrained, most boosting algorithms consist of iteratively learning weak classifiers with respect to a distribution and adding them to a final strong classifier. When they are added, they are typically weighted in some way that is usually related to the weak learners’ accuracy. After a weak learner is added, the data are reweighted: examples that are misclassified gain weight and examples that are classified correctly lose weight (some boosting algorithms actually decrease the weight of repeatedly misclassified examples, e.g., boost by majority and BrownBoost). Thus, future weak learners focus more on the examples that previous weak learners misclassified.

总结起来就是:
(1) 分步去学习weak classifier，最终的strong claissifier是由分步产生的classifier’组合‘而成的
(2) 根据每步学习到的classifier去reweight样本(分错的样本权重加大，反之减小)

流程图如下：

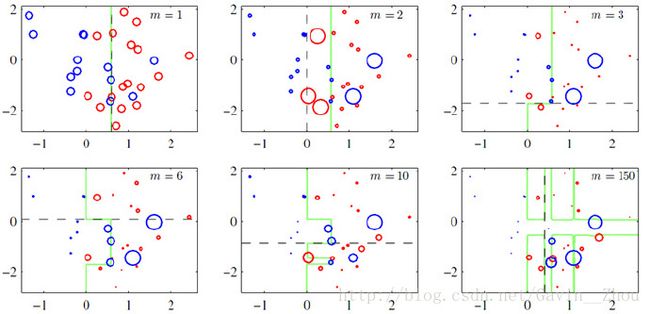
对此有个示例:

其中绿色的线表示目前取得的模型（模型是由前m次得到的模型合并得到的），虚线表示当前这次模型。每次分类的时候，会更关注分错的数据，上图中，红色和蓝色的点就是数据，点越大表示权重越高. 当m=150的时候，模型已经可以将数据正确的分来.

从上面我们可以看出Boosting和Bagging的区别，通过Gradient Boosting算法引入Bagging的思想，加上正则项，使得模型具有比一般Boosting算法(比如Adaboost)更强的robust，这也就是为什么GBDT能流行的原因

Boosting Tree

Boosting实际采用加法模型(classifier的线性组合)+前向分布，如果每次在Boosting中的基函数(classifier)使用决策树的算法就是Boosting Tree.
所以boosting tree模型就是决策树的加法模型:

其中T表示决策树.

对于回归问题的boosting tree的前向分步算法如下:

其中表示第m步之后的当前模型，此时需要求解:

对于回归问题可以使用平方误差作为损失函数L，即:

转换下就是:

其中就是当前模型拟合产生的残差(residual).

对于不是平方误差的情况，可以采用泰勒展开来进行计算，具体的可以参考xgboost作者陈天奇的介绍.
boosted tree introduction
boosted tree introduction 中文版

这里我直接摘抄下:

Obj表示object function，跟我们上面说的不一样的是，这里加上了正则，不过不影响理解.
采用泰勒展开来近似:

Gradient Boosting

Boosting更像是一种思想, gradient boosting是一种boosting的方法. 它主要的思想是，每一次建立模型是在之前建立模型损失函数的梯度下降方向.

统计学习方法中是这么说的：

假设分步模型下当前模型是f(x)，利用损失函数L的负梯度在f(x)下的值作为boosting tree算法中的残差(residual)去拟合一个回归树.

所以大概算法是这样的:

2(a)表示计算损失函数的负梯度在当前模型的值，将其作为残差的估计值;
2(b)表示估计回归树叶子节点的区域，以拟合残差的近似值;
2(c)表示利用线性搜索估计叶子节点区域的值，使得损失函数最小化;
2(d)更新回归树;

说的不好懂，没关系，下面还有个更具体的解释.

假设:

其中P表示参数，F(x;P)表示以P为参数的x的函数，也就是预测函数，在分步模型中表示为加法.

写成梯度下降的方式就是下面的形式，也就是我们将要得到的模型fm(x)的参数{am,bm}能够使得fm的方向是之前得到的模型Fm-1(x)的损失函数下降最快的方向：

Gradient Boosting是boosting思想下的一种优化的方法，首先将函数分解为可加的形式（其实所有的函数都是可加的，只是是否好放在这个框架中，以及最终的效果如何），然后进行m次迭代，通过使得损失函数在梯度方向上减少，最终得到一个优秀的模型。每次模型在梯度方向上的减少的部分，可以认为是一个“小”的或者“弱”的模型，最终我们会通过加权(也就是每次在梯度方向上下降的距离）的方式将这些“弱”的模型合并起来，形成一个更好的模型.

GBDT

一个树的定义可以分成两个部分: 结构部分和叶子权重部分.
假设q是结构映射函数把输入映射到叶子的索引号上面去，w表示叶子节点的权重. 则树可以表示为:

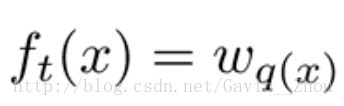
定义树的复杂度：包含两个部分树的叶子节点的个数T和叶子节点的权重的平方，即：

则此时的obj为:

此时单棵决策树的学习过程如下:

(1) 枚举所有可能的树结构q
(2) 计算对应的分数(损失值)obj，obj越小越好
(3) 找到最佳的树结构，为每个叶子节点计算权值w

然而，可能的树结构数量是无穷的，所以实际上我们不可能枚举所有可能的树结构。通常情况下，我们采用贪心策略来生成决策树的每个节点。

1. 从深度为0的树开始，对每个叶节点枚举所有的可用特征
2. 针对每个特征，把属于该节点的训练样本根据该特征值升序排列，通过线性扫描的方式来决定该特征的最佳分裂点，并记录该特征的最大收益（采用最佳分裂点时的收益）
3. 选择收益最大的特征作为分裂特征，用该特征的最佳分裂点作为分裂位置，把该节点生长出左右两个新的叶节点，并为每个新节点关联对应的样本集
4. 回到第1步，递归执行到满足特定条件为止

总结

GBDT的算法:

1. 算法每次迭代生成一颗新的决策树
2. 计算损失函数对每个样本的一阶导gi和二阶导hi
3. 通过贪心策略生成新的决策树，同时计算每个叶子节点的权重w
4. 把新生成的决策树f(x)添加到模型:
   
   为了防止过拟合添加了学习率参数(shrinkage)

---

参考博客
1. 陈天奇的博客
2. GBDT算法原理解析
3. gradient boosting解析
4. 统计学习方法(李航)
5. ensemble learning原理[推荐]
6. ensemble learning实战[推荐]
7. kaggle ensemble guide