2018-2019-1-数据结构期中考试-网络与信息安全2017

1-1

某二叉树的前序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无左孩子。(2分)

T

前序：根左右

中序：左根右

要想一样,无左孩子

1-2

采用顺序存储结构的循环队列，出队操作会引起其余元素的移动。 (2分)

 F

顺序存储不会

 

1-3

用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。 (2分)

T 

有多少个点，开多大内存

 

1-4

在用数组表示的循环队列中，front值一定小于等于rear值。 (2分)

 F

循环嘛，当然未必

 

1-5

若一个栈的输入序列为1，2，3，…，N，输出序列的第一个元素是i，则第j个输出元素是j−i−1。 (2分)

 F

i - j + 1

 

1-6

对于某些算法，随着问题规模的扩大，所花的时间不一定单调增加。 (2分)

T 

可能不变

 

1-7

若一个栈的输入序列为{1, 2, 3, 4, 5}，则不可能得到{3, 4, 1, 2, 5}这样的出栈序列。 (2分)

T   

画图试试就行

 

1-8

图的关键路径上任意活动的延期都会引起工期的延长。 (2分)

T   

关于关键路径

 

1-9

链表的每个结点都恰好有一个指针。 (2分)

 F

得看是什么链表

 

1-10

将长度分别为m,n的两个单链表合并为一个单链表的时间复杂度为O(m+n)。 (2分)

 F

时间复杂度为O(1)，如果是两个有序链表合成一个有序链表的时间复杂度为O(M + N)

 

2-1

一个递归算法必须包括（ ）。 (2分)

1. 迭代部分
2. 终止条件和迭代部分
3. 终止条件和递归部分
4. 递归部分

关于递归和迭代:

简单地说，递归是重复调用函数自身实现循环。迭代是函数内某段代码实现循环，而迭代与普通循环的区别是：循环代码中参与运算的变量同时是保存结果的变量，当前保存的结果作为下一次循环计算的初始值

2-2

通常要求同一逻辑结构中的所有数据元素具有相同的特性，这意味着（ ）。 (2分)

1. 每个数据元素都一样
2. 不仅数据元素所包含的数据项的个数要相同，而且对应数据项的类型要一致
3. 数据元素所包含的数据项的个数要相等
4. 数据在同一范围内取值

 

2-3

我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题？ (2分)

1. 拓扑排序算法
2. 深度优先搜索
3. Kruskal算法//最小生成树
4. Dijkstra算法//最短路

 

2-4

设一段文本中包含4个对象{a,b,c,d}，其出现次数相应为{4,2,5,1}，则该段文本的哈夫曼编码比采用等长方式的编码节省了多少位数？ (3分)

1. 5
2. 4
3. 2
4. 0

2-5

在一个链队列中，front和rear分别为头指针和尾指针，则插入一个结点s的操作为（ ）。(2分)

1. rear->next=s;rear=s;
2. s->next=front;front=s;
3. s->next=rear;rear=s
4. front=front->next

2-6

某队列允许在其两端进行入队操作，但仅允许在一端进行出队操作。若元素a、b、c、d、e依次入此队列后再进行出队操作，则不可能得到的出队序列是： (3分)

1. e c b a d
2. d b a c e
3. d b c a e
4. b a c d e

    根据题意判断即可（a肯定和b连着）

2-7

设计一个判别表达式左、右括号是否配对出现的算法，采用（ ）数据结构最佳。 (2分)

1. 队列
2. 线性表的链式存储结构
3. 栈
4. 线性表的顺序存储结构

2-8

由两个栈共享一个向量空间的好处是（ ）。 (2分)

1. 节省存储空间，降低下溢发生的机率
2. 减少存取时间，降低上溢发生的机率
3. 节省存储空间，降低上溢发生的机率
4. 减少存取时间，降低下溢发生的机率

     所谓上溢是满了还向里加数。下溢是没了还向里取数。共享一个空间若一个栈满了再加数就加到另一个栈里去了

2-9

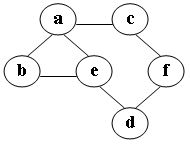
在图中自d点开始进行深度优先遍历算法可能得到的结果为： (3分)

1. d,f,c,e,a,b
2. d,e,a,c,f,b
3. d,a,e,b,c,f
4. d,a,c,f,e,b

2-10

判断一个循环队列QU（最多元素为MaxSize）为空的条件是（）。 (2分)

1. QU.front == (QU.rear + 1) % MaxSize
2. QU.front != (QU.rear + 1) % MaxSize
3. QU.front != QU.rear
4. QU.front == QU.rear

2-11

在双向循环链表结点p之后插入s的语句是： (3分)

1. s->prior=p; s->next=p->next; p->next->prior=s; p->next=s;
2. s->prior=p; s->next=p->next; p->next=s; p->next->prior=s;
3. p->next->prior=s; p->next=s; s->prior=p; s->next=p->next;
4. p->next=s; s->prior=p; p->next->prior=s ; s->next=p->next;

2-12

在决定选取何种存储结构时，一般不考虑（）。 (2分)

1. 所用编程语言实现这种结构是否方便
2. 对数据有哪些运算
3. 结点个数的多少
4. 各结点的值如何

2-13

若top为指向栈顶元素的指针，判定栈S（最多容纳m个元素）为空的条件是： (2分)

1. S->top == m-1
2. S->top == -1
3. S->top != m-1
4. S->top == 0

2-14

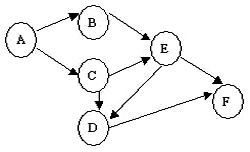
下图为一个AOV网，其可能的拓扑有序序列为： (3分)

1. ABCEDF
2. ABCDFE
3. ABCEFD
4. ACBDEF

 

2-15

若对N阶对称矩阵A以行优先存储的方式将其下三角形的元素(包括主对角线元素)依次存放于一维数组B［1..(N(N+1))/2］中，则A中第i行第j列（i和j从1开始，且i>j）的元素在B中的位序k（k从1开始）为 (3分)

1. j*(j+1)/2+i
2. i*(i+1)/2+j
3. j*(j-1)/2+i
4. i*(i-1)/2+j

 

2-16

将线性表La和Lb头尾连接，要求时间复杂度为O(1)，且占用辅助空间尽量小。应该使用哪种结构？ (2分)

1. 带头结点的双循环链表
2. 带尾指针的单循环链表
3. 单循环链表
4. 单链表

 

2-17

单链表中，增加一个头结点的目的是____。 (2分)

1. 说明单链表是线性表的链式存储
2. 标识表结点中首结点的位置
3. 方便运算的实现
4. 使单链表至少有一个结点

头结点不仅标识了表中首结点的位置，而且根据单链表(包含头结点)的结构，只要掌握了表头，就能够访问整个链表，因此增加头结点目的是为了便于运算的实现。

2-18

具有65个结点的完全二叉树其深度为（根的深度为1）： (3分)

1. 7
2. 5
3. 6
4. 8

 

2-19

若预先不知道线性表的长度，则处理线性表时较好的存储结构是（）。 (2分)

1. 顺序表
2. 静态链表
3. B和C
4. 单链表

 

2-20

设森林F中有三棵树，第一、第二、第三棵树的结点个数分别为M​1​​，M​2​​和M​3​​。则与森林F对应的二叉树根结点的右子树上的结点个数是： (3分)

1. M​2​​+M​3​​
2. M​1​​+M​2​​
3. M​3​​
4. M​1​​