TSP_旅行商问题 - 遗传算法（四）
本文修改日志：
2017.01.22：整理并发布第一版博文；
2018.05.01：修改源代码170行（添加float），double RateVariation = float(rand()%100)/100;
一、前言
【旅行商问题】旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。【百度百科】
旅行商求解系列：
-------------------------------------------------------------------------------------------------
（1）TSP_旅行商问题- 蛮力法( 深度遍历优先算法DFS )
（2）TSP_旅行商问题- 动态规划
（3）TSP_旅行商问题- 模拟退火算法
（4）TSP_旅行商问题- 遗传算法
（5）TSP_旅行商问题- 粒子群算法
（6）TSP_旅行商问题- 神经网络
-------------------------------------------------------------------------------------------------
二、本文概要
本文基于遗传算法的思想解决旅行商问题，满足了时间复杂度可接受，而且又不会陷入局部最优。本文首先简要介绍了遗传算法（GA）以及核心思想，此外，还给出具体实现程序的具体数据结构（最后提供本文的完整的代码以及整个工程的资源）。然后重点介绍了遗传算法的总体设计以及算法的详略流程，还结合代码重点介绍了遗传算法的几大核心部分，包括“选择（父代）”，“交叉”，“个体变异”，“更新种群（自然选择或者精英保留法）”等。最后根据实验代码给出实验结果，并对本文做出总结。
三、遗传算法
1. 遗传算法简介（GA）
模拟进化计算（Simulated Evolutionary Computation) 是近二十年来信息科学、人工智能与计算机科学的一大研究领域，由此所派生的求解优化问题的仿生类算法（遗传算法、演化策略、进化程序），由于其鲜明的生物背景、新颖的设计原理、独特的分析方法和成功的应用实践，正日益形成全局搜索与多目标优化理论的一个崭新分支。
遗传算法(GeneticAlgorithm ，GA )是通过模拟生物进化过程来完成优化搜索的，由美国J. Holland 教授提出的一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。它起源于达尔文的进化论，是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。其主要特点是群体搜索策略和群体中个体之间的信息交换，搜索不以梯度信息为基础。它尤其适用于处理传统搜索方法难于解决的复杂和非线性问题，可广泛应用于组合优化、机器学习、自适应控制、规划设计和人工生命等领域。作为一种全局优化搜索算法，遗传算法以其简单通用、鲁棒性强、适于并行处理以及应用范围广等特点，使其成为21 世纪智能计算核心技术之一。进入80 年代，遗传算法迎来了兴盛发展时期，无论是理论研究还是应用研究都成了十分热门的话题。
2. 用遗传算法解决旅行商问题（GA solve the TSP problem）
目前针对TSP问题有许多种解法，较为常用的算法有神经网络法、列表寻优法、二叉树描述法、模拟退火法和遗传算法等等。遗传算法是近几年发展起来的一种崭新的全局优化算法，它借用了生物遗传学的观点，通过选择、遗传、变异和免疫等作用机制，使每个个体的适应性提高。由于其全局搜索的特性，遗传算法在解决TSP问题中有着其他算法所没有的优势。提出的TSP问题包括31个城市的编号和各自的位置。本文基于遗传算法解决TSP问题并进行编程和问题求解。
3. 遗传算法核心思想
模拟进化算法的核心思想源于这样的基本认识：体现在“优胜劣汰”这一自然规律的生物进化过程本身是一个自然的、并行发生的、鲁棒的优化过程，这一优化过程的目标是对环境的适应性（fitness)，而生物种群通过生物体的遗传、变异来达到优化（亦即进化）之目的，对生物进化的这种优化观点早在六十年代就引起J.H.Holland、I.Recenberg及L.J.Fogel等计算智能学者的特别兴趣,并相继创立了现在被称之为遗传算法(genetic algorithms)、演化策略(evolution strategies)和进化程序(evolutionary programming)的模拟进化算法。
- 参数的设置，确定个体的编码方式（二进制或者其他）
- 初始随机解的生成
- 选择算子：选择父代的策略（轮盘赌策略）
- 繁殖：交叉两个父代并产生新个体（TSP问题的编码，需要解决路径冲突问题，即保证每个城市有且仅遍历一次）
- 变异：对新个体进行变异操作
- 竞争（更新种群）：精英保留策略或者自然选择
4. 本文使用的数据结构以及GA相关参数
#define CITY_NUM 150 // TSP_城市个数
#define GROUP_NUM 30 // 群体规模
#define SON_NUM 32 // 产生儿子的个数 SON_NUM = GROUP_NUM + 2
const double P_INHERIATANCE = 0.01; // 变异概率
const double P_COPULATION = 0.8; // 杂交概率
const int ITERATION_NUM = 1500; // 遗传次数(迭代次数)
const double MAX_INT = 9999999.0;
typedef struct{
int vex_num, arc_num; // 顶点数 边数
int vexs[CITY_NUM]; // 顶点向量
double arcs[CITY_NUM][CITY_NUM]; // 邻接矩阵
}Graph;
typedef struct{
double length_path;
int path[CITY_NUM];
double P_Reproduction;
}TSP_solution;四、程序流程
1. 遗传算法总体设计
- 步骤一、初始化参数；
- 步骤二、随机产生一组初始个体构成的初始种群，并评价每一个个体的适配值（路径长度决定）；
- 步骤三、判断算法的收敛准则是否满足（此处为迭代次数）。若满足输出搜索结果；否则执行[4-8]步骤；
- 步骤四、执行选择操作（随机选择两个种群个体），使用【轮盘赌选择】思想，每次按照概率大小随机返回当前群体中的某个个体的下标；
- 步骤五、按杂交概率const double P_COPULATION = 0.8;执行交叉操作；
- 步骤六、对子群Son_solution[]进行变异处理，产生随机数RateVariation，小于变异概率P_INHERIATANCE时，进行变异处理（随机交换两个城市的位置）；
- 步骤七、更新Son_solution[]的路程和概率Calc_Probablity(G, total_length)；
- 步骤八、采用“父子混合选择”更新群体（精英保留策略）；
- 步骤九、返回步骤（2）判断是否进行下一次迭代；
说明：
- 本算法的结束准则是根据指定了的迭代次数，当算法达到迭代次数时，算法结束，输出当前的最优解；
- 在根据适配值计算并选择的时候，记录下来的当前最优值，在变异后加入跟新的群体，保证新的迭代循环中TSP解越来越好（不会变差）；
- 在选择的一种操作是拿最优的K个替换最差的K个子个体，本例是按适配值选择，并使群体数目变少，当每次变异操作后，产生随机路径补充群体是群体数目不变，再次循环，一定程度上防止因初始群体的选择问题而陷入局部最优。
2. 总体流程图
遗传算法总体流程设计
3. 详细流程图
遗传算法详细流程图（来源于百度图片）
五、程序开发 - 遗传算法解决TSP问题
1. 随机生成初始种群：
void InitialGroup(Graph G){
cout<<"----------------------【遗传算法参数】-----------------------"<2. 遗传算法函数：
void TSP_Evolution(Graph G){
/* */
int iter = 0;
while(iter < ITERATION_NUM){
// cout<<"***********************【第次"<<(iter + 1)<<"迭代】*************************"< 自交( 父母为同一个个体时, 母亲重新选择, 直到父母为不同的个体为止 )
cout<<"Warning!【Father_index = Mother_index】"<= GROUP_NUM
int M = GROUP_NUM - GROUP_NUM/2;
Length_SonSoliton = 0; // 遗传产生的个体个数, 置零重新累加
while(M){
double Is_COPULATION = ((rand()%100 + 0.0) / 100);
if (Is_COPULATION > P_COPULATION)
{
// cout<<"[ 这两个染色体不进行杂交 ]Is_COPULATION = "< 3. 选择算子：
// 选择
/*
输入：当前总群
输出：按照一个评价, 随机从当前总群筛选出杂交对象, 本程序每次返回一个个体
选择方案：比例选择规则, [轮盘赌选择]
机制：反映在对父代种群中每一个体所赋予的允许繁殖概率及其从2M个中间个体中如何选择子代种群的机制上！
*/
/*
[轮盘赌选择] - 轮盘赌选择是从染色体群体中选择一些成员的方法，被选中的机率和它们的适应性分数成比例，染色体的适应性分数愈高，被选中的概率也愈多.
1. 随机产生一个概率 selection_P
2. [概率分布函数]声明变量 distribution_P = 0, 对于每个个体, 依次累加个体的概率到distribution_P上, 判断当前随机概率selection_P是否小于distribution_P, 若是则中该染色体, 结束循环
*/
int Evo_Select(Graph G){
double selection_P = ((rand()%100 + 0.0) / 100);
// cout<<"selection_P = "<4. 繁殖（交叉操作）：
// 交叉
/*
输入：[TSP_Father , TSP_Mother]两个个体作为父母, 进行杂交
输出：通过杂交产生新个体(遗传算法产生2个新个体, 演化算法产生1个新个体)
杂交方案：[父子混合选择][自然选择 - 父母不参与竞争]
-- [演化策略]所使用的杂交算子是从两个个体生成一个个体的操作
-- [遗传算法]生成两个新个体。常见的“中间杂交”（intermediate crossover）及“随机杂交”（random crossover）等!
*/
/*
TSP_杂交具体方法：
1. 随机选取两个交叉点i和j,记为 Father_Cross 和 Mother_Cross
2. 将两交叉点中间的基因段互换
3. 分别对Father和Mother的路径进行冲突处理：
-- 以Father为例, 保持Father_Cross基因段不变, 基因段以外的部分与Father_Cross基因段冲突的城市, 用Father_Cross和Mother_Cross对应的位置去互换, 直到没有冲突.
-- 冲突城市的确定: Father_Cross 和 Mother_Cross去补集,存放于数组 Conflict[] 中.
*/
void Evo_Cross(Graph G, TSP_solution TSP_Father, TSP_solution TSP_Mother){
// 杂交过程：随机产生杂交的位置, 保证 IndexCross_i < IndexCross_j【全局变量】
IndexCross_i = rand() % (CITY_NUM - 1) + 1; // 不能取到起始城市
IndexCross_j = rand() % (CITY_NUM - 1) + 1; //
if (IndexCross_i > IndexCross_j)
{
int temp = IndexCross_i;
IndexCross_i = IndexCross_j;
IndexCross_j = temp;
}
if (IndexCross_j == CITY_NUM || IndexCross_i == 0)
{
cout<<"[ 杂交过程的随机数产生有问题... ]"<5. 个体变异：
// 变异
/*
输入：杂交得到的所有个体（大于总群规模）
输出：通过变异策略, 以一定的变异概率（确定变异个数）随机选择个体进行变异
变异策略：随机交换染色体的片段, TSP - 随机交换两个城市的位置
*/
void Evo_Variation(Graph G, int Index_Variation){
// 随机产生两个随机数表示两个城市的位置, 并进行位置交换
int City_i = (rand() % (CITY_NUM - 1)) + 1; // [1, CITY_NUM - 1]起始城市不变异
int City_j = (rand() % (CITY_NUM - 1)) + 1; //
while(City_i == City_j){
City_j = (rand() % (CITY_NUM - 1)) + 1;
}
// 交换城市位置 - 变异
int temp_City = Son_solution[Index_Variation].path[City_i];
Son_solution[Index_Variation].path[City_i] = Son_solution[Index_Variation].path[City_j];
Son_solution[Index_Variation].path[City_j] = temp_City;
}6. 更新种群（精英保留策略）：
// 父代 - TSP_Groups[]
// 子代 - Son_solution[]
void Evo_UpdateGroup(Graph G){
TSP_solution tempSolution;
// 先对子代 - Son_solution[] 依据路径长度进行排序 - 降序[按路径从大到小]
for (int i = 0; i < Length_SonSoliton; i++)
{
for (int j = Length_SonSoliton - 1; j > i; j--)
{
if ( Son_solution[i].length_path > Son_solution[j].length_path )
{
tempSolution = Son_solution[i];
Son_solution[i] = Son_solution[j];
Son_solution[j] = tempSolution;
}
}
}
// 更新
for (int i = 0; i < Length_SonSoliton; i++) // 子代 - 按路径从大到小排序
{
for (int j = 0; j < GROUP_NUM; j++) // 父代
{
if ( Son_solution[i].length_path < TSP_Groups[j].length_path )
{
TSP_Groups[j] = Son_solution[i]; // 种群更新
break;
}
}
}
TSP_Evaluate(G);
}7. 以概率的形式计算个体优先级（路径越短概率越高）：
// 处理对象：每次新产生的群体, 计算每个个体的概率
// 问题：解决TSP问题, 路径越短概率应该越高
// 方案：对于当前总群, 将所有个体路径取倒数, 然后乘以该总群的总路径得到大于1的值, 然后进行归一化, 取得概率
// 归一化：累加当前所有大于1的个体的伪概率, 得到TempTotal_P, 每个概率再分别除以 TempTotal_P 进行归一化
void Calc_Probablity(Graph G, double total_length){
double TempTotal_P = 0.0;
for (int i = 0; i < GROUP_NUM ;i++)
{
TSP_Groups[i].P_Reproduction = (1.0 / TSP_Groups[i].length_path ) * total_length;
TempTotal_P += TSP_Groups[i].P_Reproduction;
}
for (int i = 0;i < GROUP_NUM; i++)
{
TSP_Groups[i].P_Reproduction = TSP_Groups[i].P_Reproduction / TempTotal_P;
}
}8. 评价函数：
/*
// TSP - 评价函数
// 输入：当前总群 TSP_Groups[] - 包括 每个个体的路径和所需的长度
// 输出：当前总群中, 最优的个体：bestSolution
// 评价方法：路径最短的为最优
*/
void TSP_Evaluate(Graph G){
TSP_solution bsetSolution;
bsetSolution = TSP_Groups[0];
for (int i = 1; i < GROUP_NUM; i++)
{
if (bsetSolution.length_path > TSP_Groups[i].length_path)
{
bsetSolution = TSP_Groups[i];
}
}
}9. 处理冲突：
TSP_solution Handle_Conflict(Graph G, TSP_solution ConflictSolution, int *Detection_Conflict, int *Model_Conflict, int Length_Conflict){
/*
cout<<"[ Handle_Conflict ]"< ";
}
cout< ConflictSolution
// 8 7 [4 5 6 7 1] 9 6 5
// [0 3 2] --> Detection_Conflict
// [4 5 6] --> Model_Conflict
// 解决冲突, index 为当前i冲突的位置, 用Model_Conflict去替换.
// cout<<"index = "<10. 计算程序耗时：
#include
int main(){
time_t T_begin = clock();
// 耗时程序段
time_t T_end = clock();
double RunningTime = double(T_end - T_begin) / CLOCKS_PER_SEC;
cout<
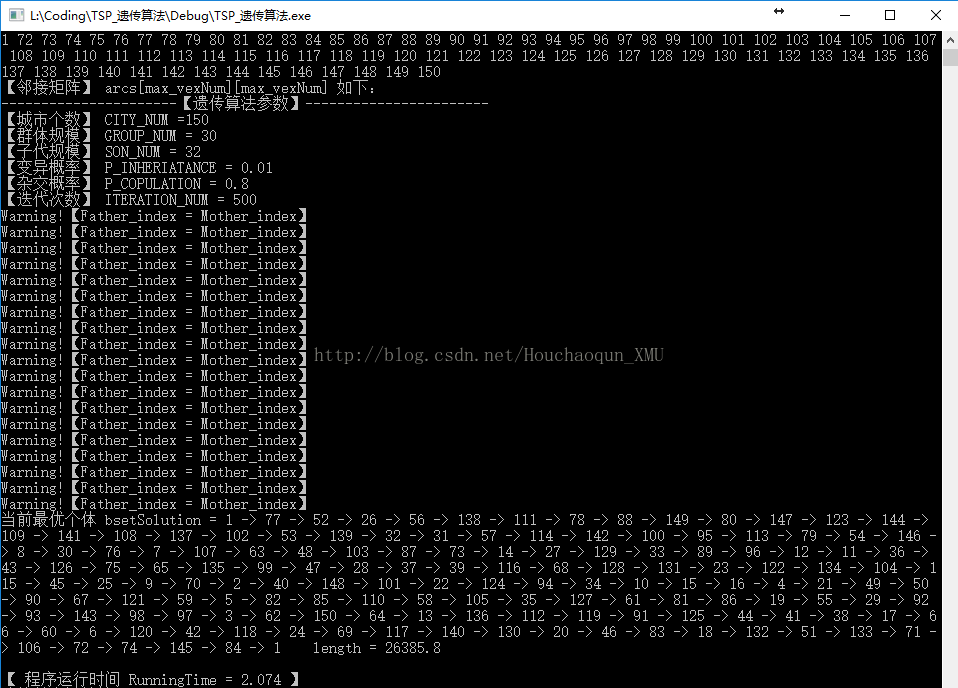
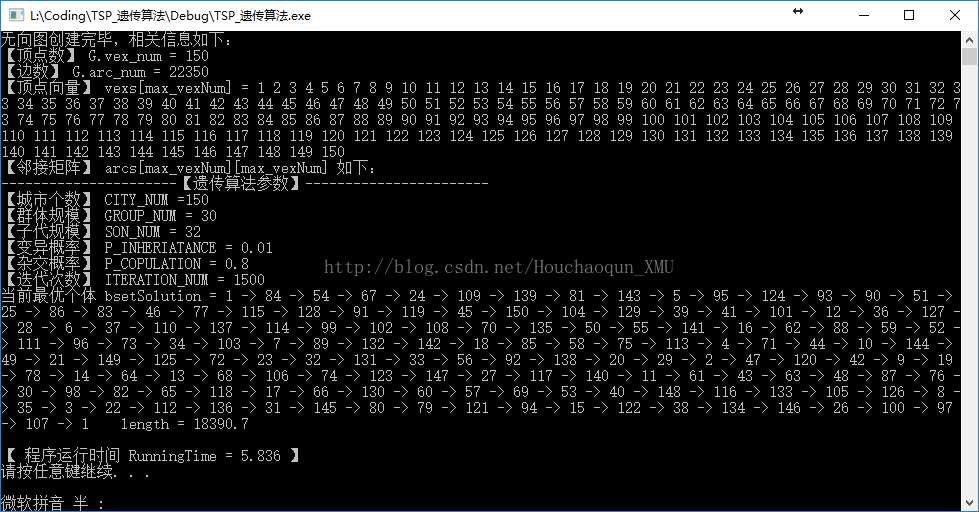
六、测试数据及其运行结果
1. 测试数据：由150个城市组成，（由于数据量太大，以txt的形式共享，点击这里下载）
150个城市组合的TSP（部分数据）
2. 运行结果及其分析：
迭代次数为500时，程序耗时2.074秒，所得最有路径为26385.8
迭代次数为1500时，程序耗时5.836秒，所得最有路径为18390.7（近似全局最优解）
七、总结
1. 总结：
- 【GA与模拟退火算法的区别】模拟退火是采用单个个体进行优化，解的优化不易陷入局部极小，对整个解空间的覆盖不够，依赖初始参数的设置。遗传算法是一种群体性算法，具有并行性，全局搜索能力极强，局部搜索能力差。参数的选择对算法性能影响很大，并且需要对问题进行编码。
- 【GA与模拟退火算法的相同点】两者均属于概率搜索算法。均需要平衡局部搜索与全局搜索，从而避免过早陷入局部搜索。算法的鲁棒性强，对目标函数及约束函数的形式没有严格要求，不需要其可导、连续等解析性质。两种算法均易于与其它启发式算法相融合。
- 【应用研究领域】函数优化，组合优化，生产调度问题，自动控制，机器人智能控制，图象处理和模式识别。
- 【展望】本文实现较简单的遗传算法，还有许多可以优化的地方，由于时间原因未进一步研究，在此不做详细介绍，有兴趣的同学可以加以改进！
2. 遗传算法相关经验参数：
| 遗传算法相关参数 | 经验值 |
| 总群规模M | 20 -- 100 |
| 交叉概率 | 0.4 -- 0.99 |
| 变异概率 | 0.0001 -- 0.1 |
| 遗传过程的迭代次数 | 100 -- 1000 |
3. 遗传算法的优缺点：（尚待完善，后续补充）
-- 优点：
1）具有较强的全局搜索能力
2）隐含并行性
3）在计算精度要求较高时，计算时间少
-- 缺点：
1）易陷入局部早熟
2）收敛性能差
2）收敛性能差
3）由连续问题归纳到组合问题求解，使得精度受到很大的影响
八、程序源码
1. GA.h
#ifndef _GA_H_
#define _GA_H_
#define CITY_NUM 150 // TSP_城市个数
#define GROUP_NUM 30 // 群体规模
#define SON_NUM 32 // 产生儿子的个数 SON_NUM = GROUP_NUM + 2
const double P_INHERIATANCE = 0.01; // 变异概率
const double P_COPULATION = 0.8; // 杂交概率
const int ITERATION_NUM = 1500; // 遗传次数(迭代次数)
const double MAX_INT = 9999999.0;
typedef struct{
int vex_num, arc_num; // 顶点数 边数
int vexs[CITY_NUM]; // 顶点向量
double arcs[CITY_NUM][CITY_NUM]; // 邻接矩阵
}Graph;
typedef struct{
double length_path;
int path[CITY_NUM];
double P_Reproduction;
}TSP_solution;
TSP_solution TSP_Groups[GROUP_NUM]; // 存储群体
TSP_solution Son_solution[SON_NUM]; // 存储杂交后的个体
int Length_SonSoliton = 0; // 遗传产生的孩子的个数
void CreateGraph(Graph &G);
void InitialGroup(Graph G);
double CalculateLength(Graph G,TSP_solution newSolution);
void TSP_Evolution(Graph G); // 模拟生物进化 - 解决TSP问题
int Evo_Select(Graph G); // 选择函数
void Evo_Cross(Graph G, TSP_solution TSP_Father, TSP_solution TSP_Mother); // 杂交函数
void Evo_Variation(Graph G, int Index_Variation); // 变异函数
void Evo_UpdateGroup(Graph G);
void TSP_Evaluate(Graph G); // TSP - 评价函数
int *Get_Conflict(int Conflict_Father[], int Conflict_Mother[], int Length_Cross, int &Length_Conflict); // 返回冲突的数组
TSP_solution Handle_Conflict(Graph G, TSP_solution ConflictSolution, int *Detection_Conflict, int *Model_Conflict, int Length_Conflict); // 解决冲突
void Calc_Probablity(Graph G, double total_length); // 计算概率
bool Check_path(Graph G, TSP_solution CurrentSolution);
void Display(Graph G);
#endif2. GA.cpp
#include
#include
#include // 本文用于输出对齐
#include
#include
#include
#include "GA.h"
using namespace std;
int IndexCross_i;
int IndexCross_j;
int main(){
time_t T_begin = clock();
Graph G;
CreateGraph(G);
srand ( unsigned ( time(0) ) );
InitialGroup(G);
TSP_Evolution(G); // 遗传算法
time_t T_end = clock();
double RunningTime = double(T_end - T_begin) / CLOCKS_PER_SEC;
cout<> G.vex_num;
// read_in >> G.arc_num;
G.arc_num = 0;
for (int i = 0;i < G.vex_num; i++)
{
read_in >> G.vexs[i];
}
G.vexs[G.vex_num] = '\0'; // char的结束符.
for (int i = 0; i < G.vex_num;i++)
{
for (int j = 0; j < G.vex_num; j++)
{
read_in >> G.arcs[i][j];
// calculate the arc_num
if (G.arcs[i][j] > 0)
{
G.arc_num++;
}
}
}
// display
cout<<"无向图创建完毕，相关信息如下："< 自交( 父母为同一个个体时, 母亲重新选择, 直到父母为不同的个体为止 )
// cout<<"Warning!【Father_index = Mother_index】"<= GROUP_NUM
int M = GROUP_NUM - GROUP_NUM/2;
Length_SonSoliton = 0; // 遗传产生的个体个数, 置零重新累加
while(M){
double Is_COPULATION = ((rand()%100 + 0.0) / 100);
if (Is_COPULATION > P_COPULATION)
{
// cout<<"[ 这两个染色体不进行杂交 ]Is_COPULATION = "< ";
}
cout< IndexCross_j)
{
int temp = IndexCross_i;
IndexCross_i = IndexCross_j;
IndexCross_j = temp;
}
if (IndexCross_j == CITY_NUM || IndexCross_i == 0)
{
cout<<"[ 杂交过程的随机数产生有问题... ]"< ConflictSolution
// 8 7 [4 5 6 7 1] 9 6 5
// [0 3 2] --> Detection_Conflict
// [4 5 6] --> Model_Conflict
// 解决冲突, index 为当前i冲突的位置, 用Model_Conflict去替换.
// cout<<"index = "< ";
}
cout< ";
}
cout<九、参考文献
- 胡妙娟，胡春，钱锋，遗传算法中选择策略的分析
- 本文相关代码以及数据：http://download.csdn.net/detail/houchaoqun_xmu/9740071
- 白话讲解遗传算法 (Genetic Algorithm)：http://blog.chinaunix.net/uid-27105712-id-3886077.html
- Study on Fuzzy Classifier Based on Genetic Algorithm Optimization
- Feature Selection Based on Hybridization of Genetic Algorithm and Particle Swarm Optimization
- A genetic algorithm-based learning approach to understand customer satisfaction with OTA websites
- Boolean regulatory network reconstruction using literature based knowledge with a genetic algorithm optimization method