Focal Loss学习笔记

Focal Loss

论文链接：https://arxiv.org/abs/1708.02002

论文指出one-stage detector准确率低的原因是训练中foreground 和background类别数量的极大不均衡（1:1000）。

Focal loss在标准交叉熵损失基础上修改得到。这个函数可以通过减少易分类样本的权重，使得模型在训练时更专注于难分类的样本。

Cross Entropy

以二分类为例，下面是交叉熵损失。$y\in \{\pm 1\}$为GT的值。$p\in [0,1]$为模型预测$y=1$的概率。

$CE(p,y)=\{\begin{array}{ll}-log(p)& ify=1\\ -log(1-p)& otherwise\end{array}$

为了方便表示，我们定义$p_t=\{\begin{array}{ll}p& ify=1\\ 1-p& otherwise\end{array}$

所以有$CE(p,y)=CE(p_t)=-\log (p_t)$

下图蓝色的线代表了CE loss。可以看出被很好分类的样本有较小的loss，但大量的这样的loss的和将占大部分的总loss。

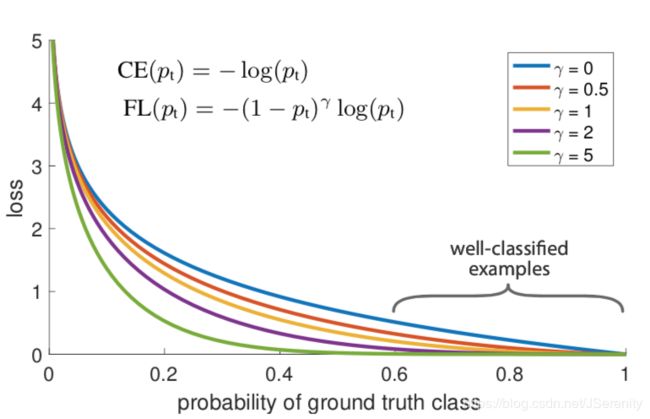
Balanced Cross Entropy

一个解决类别不平衡的方法是加入一个权重系数$\alpha \in [0,1]$
${\alpha }_t=\{\begin{array}{ll}\alpha & ify=1\\ 1-\alpha & otherwise\end{array}$

$CE(p_t)=-{\alpha }_t\log (p_t)$

举个例子。如果有大量的$y=1$的情况，设$\alpha =0.3$。y = 1的时候loss会乘以0.3，y = -1的时候loss乘以0.7，使得y = 1的loss变得小一些。这样，y的类别的不平衡会得到改善。论文将这个方法作为研究focal loss实验的baseline。

Focal Loss Definition

实验表明大量易分类的loss构成了主要loss并主导梯度下降。$\alpha$平和了正/负样本的重要度，但没有平衡易/难分类样本的重要度。所以我们提出了一个降低易分类样本的方法，让训练注意力集中在难分类的样本上。在交叉熵损失上添加一个变换因子$(1-p_t{)}^{\gamma }$ $(\gamma \ge 0)$。我们定义focal loss如下：

$FL(p_t)=-(1-p_t{)}^{\gamma }\log (p_t)$

可以在上面的图片中看到$\gamma \in [0,5]$的focal loss的图像。当样本被误分类$p_t$比较小的时候，变换因子接近1，loss接近不变。当$p_t\to 1$的时候，变换因子接近0，给被很好分类的样本一个很小的权重。这样就提高了对误分类样本的关注度，这也是这个方法名字的含义。$\gamma$可以控制变换因子的速率，当$\gamma =0$时，FL退化成CE。

实际使用中focal loss结合了$\alpha$-balanced，因为实验表明这样会略微提高精度：

$FL(p_t)=-\alpha (1-p_t{)}^{\gamma }\log (p_t)$