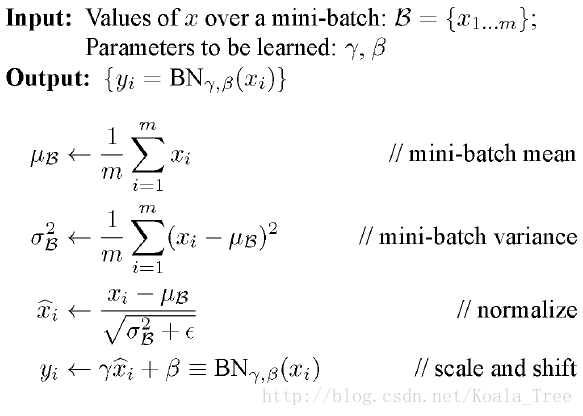卷积神经网络CNN-基础

卷积神经网络CNN-基础

1. 链式反向梯度传导

链式法则的计算

y=f(x)，z=g(y)∂z∂x=∂z∂y⋅∂y∂x

简单函数的例子

f(x,y,z)=(x+y)⋅z

记： q=x+y，f=q⋅z 。
则有：

∂f∂z=q，∂f∂q=z∂q∂x=1，∂q∂y=1

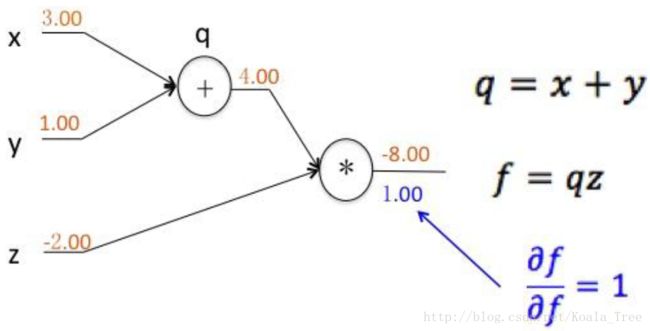
函数 f 对自己的导数为1，上面的数字代表各层传递的值。

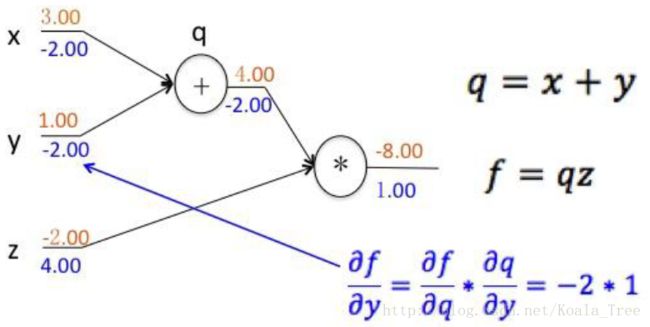
从后向前反向传播，得到反向梯度传导的导数值。

layer融合的过程中，如果layer是相加的，则直接传递导数；如果是相乘，则相互交换导数。

复杂函数的例子

f(x,y,w)=1exp{−[(x1+x2)w+max(y1,y2)]}

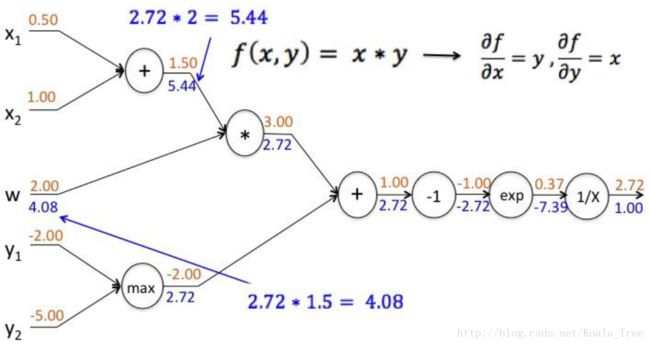
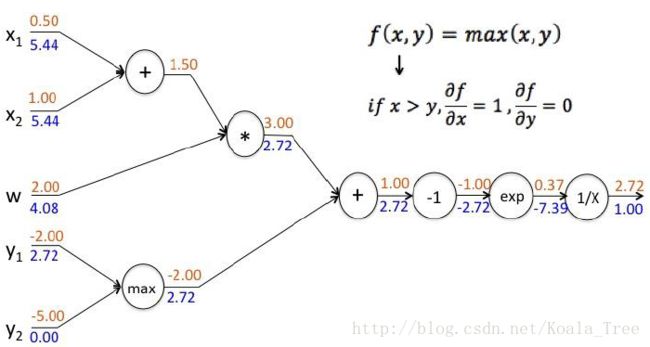
对每层的导数（ Δy，Δx ）结果进行存储，用于下一层的导数计算。

2. 卷积层

卷积层的定义

卷积层由多个卷积核组合形成，每个卷积核同输入数据进行卷积运算，形成新的特征图。

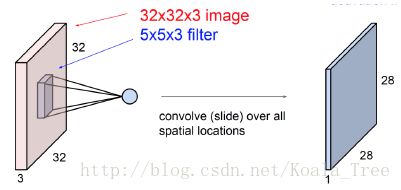
每一个卷积核，仅产生一层特征图。有多少个卷积核，下一层便产生特征图的“厚度“即为对应的个数。

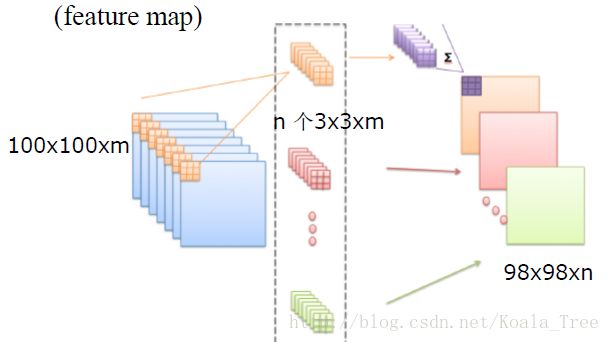
卷积核

• 同输入数据进行计算的二维（一维，三维）算子；
• 其大小有用户定义，其深度根据输入的数据深度大小确定；
• 卷积核的“矩阵”值，便为卷积神经网络的参数，及网络需要学习的参数；
• 卷积核初值随机生成，通过反向传播进行更新。
  -

卷积层关键参数

• 卷积核的大小：
  
  • 一般卷积核会选择奇数，满足对称，偶数也可以；
  • 一般会选择卷积核小一些，层数多一些的结构来建立卷积神经网络模型。
  • 1×1×n大小的卷积核可以用做特殊的降维处理。 **
  • 卷积核的“厚度”与前一层输入数据的“厚度”保持一致；
  • 一般卷积核会覆盖全部输入，特殊情况下覆盖局部区域。
• 步长
  步长（stride）表示对输入特征图的扫描间隔对输出特征图的影响。
  步长大的情况相当于在卷积的过程中做了池化。
• 边界扩充（pad）
  在卷积计算过程中，为了允许边界上的数据也能作为中心参与卷积运算，将边界假装延伸。
  
  • 扩充的目的是为了确保卷积后特征图尺度一致；
  • 卷积核的宽度为 2i+1 ，则添加pad的宽度为 i 。
• 卷积神经网络的“宽度”
  一般常见的参数为64、128、256。主要是为了GPU并行计算，使得训练过程更加高效。

卷积网络

• 卷积网络的参数计算
  
  • Num： n×3×3×m ， n 个 3×3×m 大小的卷积核。
  • 与传统的神经网络相比，其参数的数量会减少，但是其计算量会增加。
• 正向传播（Forward Propagation）
• 反向传播（Back Propagation）

3. 功能层

卷积神经网络需要的一些额外功能：
* 非线性激励：卷积是线性运算，增加非线性描述的能力；
* 降维：特征图稀疏，减少数据运算量，保持精度；
* 归一化：特征的scale保持一致；
* 区域分割：不同区域进行独立学习；
* 区域融合：对分开的区域进行合并，方便信息融合；
* 增维：增加图片生成或探测任务中空间信息。

非线性激励层

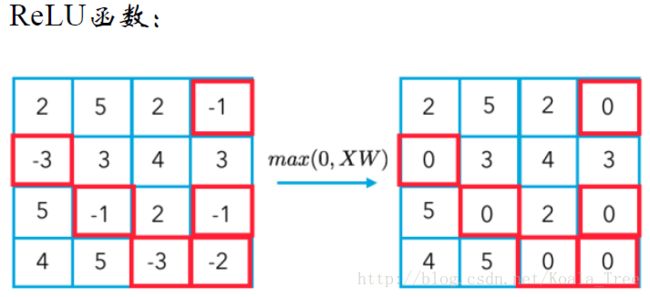
在输入的特征图和卷积核卷积的过程中，每一次卷积计算都会生成特征图的一个值，卷积计算为线性运算，需要将所得结果输入非线性激励函数中，得到一个非线性值，增加非线性描述的能力。
一般会使用ReLU函数，相当于选取 XW 和 0 两者之间的最大值。

池化层

• 数据降维，方便计算和存储；
• 池化过程中，每张特征图单独降维。

归一化层

在计算的过程中，中间层部分激励不平等，则对数据进行归一化。某种程度上可以减少梯度衰减。

• 批量归一化Batch Normalization(BN)
  
  • 可以加速训练过程，提高精度。
    
• 近邻归一化Local Response Normalization
  
  xi=xi(k+(α∑jx2j))β
  
  与BN的区别：
  
  • BN依据mini batch的数据，近邻归一化仅需要自身；
  • BN训练中有学习参数。

切分层

在某些应用中，希望独立对某些区域单独学习。
其好处是，学习多套参数，其具有更强的特征描述能力。

融合层

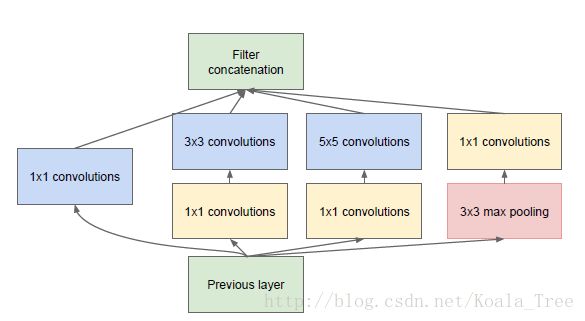
对独立进行特征学习的分支进行融合，构建高效且精简的特征组合。
例如：GoogleLeNet 的基本模块用多种分辨率对目标特征进行学习，之后进行多分辨率特征的融合。

• 级连 - concatenation
  不同输入网络特征简单叠加。
  

  

• 合并 - 运算融合形状一致的特征层，通过（+，-，X， max，conv）运算，形成形状相同的输出。
  ResNet的融合：
  

  

4. 卷积神经网络MNIST

下面还是利用mnist数据集，利用卷积神经网络进行手写字体的识别。

代码

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

import tensorflow as tf

# Parameters
learning_rate = 0.001
training_epochs = 30
batch_size = 100
display_step = 1

# Network Parameters
n_input = 784 # MNIST data input (img shape: 28*28)
n_classes = 10 # MNIST total classes (0-9 digits)

# tf Graph input
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])

#pre-define the  
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')


# Create model
def multilayer_perceptron(x, weights, biases):
    #now, we want to change this to a CNN network

    #first reshape the data to 4-D
    x_image = tf.reshape(x, [-1,28,28,1])

    #then apply cnn layers

    h_conv1 = tf.nn.relu(conv2d(x_image, weights['conv1']) + biases['conv_b1'])
    h_pool1 = max_pool_2x2(h_conv1)

    h_conv2 = tf.nn.relu(conv2d(h_pool1, weights['conv2']) + biases['conv_b2'])
    h_pool2 = max_pool_2x2(h_conv2)

    h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
    h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, weights['fc1']) + biases['fc1_b'])


    # Output layer with linear activation
    out_layer = tf.matmul(h_fc1, weights['out']) + biases['out_b']
    return out_layer

# Store layers weight & biases
weights = {
    'conv1': tf.Variable(tf.random_normal([5, 5, 1, 32])),
    'conv2': tf.Variable(tf.random_normal([5, 5, 32, 64])),
    'fc1' : tf.Variable(tf.random_normal([7*7*64,256])),
    'out': tf.Variable(tf.random_normal([256,n_classes]))
}
biases = {
    'conv_b1': tf.Variable(tf.random_normal([32])),
    'conv_b2': tf.Variable(tf.random_normal([64])),
    'fc1_b': tf.Variable(tf.random_normal([256])),
    'out_b': tf.Variable(tf.random_normal([n_classes]))
}

# Construct model
pred = multilayer_perceptron(x, weights, biases)

# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)

# Initializing the variables
init = tf.global_variables_initializer()

# Launch the graph
with tf.Session() as sess:
    sess.run(init)

    # Training cycle
    for epoch in range(training_epochs):
        avg_cost = 0.
        total_batch = int(mnist.train.num_examples/batch_size)
        # Loop over all batches
        for i in range(total_batch):
            batch_x, batch_y = mnist.train.next_batch(batch_size)
            # Run optimization op (backprop) and cost op (to get loss value)
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_x,
                                                          y: batch_y})
            # Compute average loss
            avg_cost += c / total_batch
        # Display logs per epoch step
        if epoch % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
    print("Optimization Finished!")

    # Test model
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # Calculate accuracy
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
    print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))

关键代码解释

1.：tf.nn.conv2d

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)

除去name参数用以指定该操作的name，与方法有关的一共五个参数：

• 第一个参数input：指需要做卷积的输入图像，它要求是一个Tensor，具有[batch, in_height, in_width, in_channels]这样的shape，具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]，注意这是一个4维的Tensor，要求类型为float32和float64其中之一；
• 第二个参数filter：相当于CNN中的卷积核，它要求是一个Tensor，具有[filter_height, filter_width, in_channels, out_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]，要求类型与参数input相同，有一个地方需要注意，第三维in_channels，就是参数input的第四维；
• 第三个参数strides：卷积时在图像每一维的步长，这是一个一维的向量，长度4；对于图片，因为只有两维，通常strides取[1，stride，stride，1]；
• 第四个参数padding：string类型的量，只能是”SAME”,”VALID”其中之一，这个值决定了不同的卷积方式。’SAME’时，表示卷积核可以停留在图像边缘，即图片的大小不会因为卷积运算而变小；’VALID’时，表示卷积核不能停留在图像边缘，即会因为卷积运算图片的大小会缩小；
• 第五个参数：use_cudnn_on_gpu :bool类型，是否使用cudnn加速，默认为true。
  结果返回一个Tensor，这个输出，就是我们常说的feature map.

2.：tf.nn.max_pool

tf.nn.max_pool(value, ksize, strides, padding, name=None)

• 第一个参数value：需要池化的输入，一般池化层接在卷积层后面，所以输入通常是feature map，依然是[batch, height, width, channels]这样的shape；
• 第二个参数ksize：池化窗口的大小，取一个四维向量，一般是[1, height, width, 1]，因为我们不想在batch和channels上做池化，所以这两个维度设为了1；
• 第三个参数strides：和卷积类似，窗口在每一个维度上滑动的步长，一般也是[1, stride,stride, 1]；
• 第四个参数padding：和卷积类似，可以取’VALID’ 或者’SAME’。
  返回一个Tensor，类型不变，shape仍然是[batch, height, width, channels]这种形式。

3.：tf.reshape

tf.reshape(tensor, shape, name=None) 

函数的作用是将tensor变换为参数shape的形式。
其中shape为一个列表形式，特殊的一点是列表中可以存在-1。-1代表的含义是不用我们自己指定这一维的大小，函数会自动计算，但列表中只能存在一个-1。

版权声明：本博客为博主学习网课《深度学习》课程总结，博文图片均为课程PPT图片。
同时，本文为博主原创文章，博客地址：http://blog.csdn.net/koala_tree，未经博主允许不得转载。