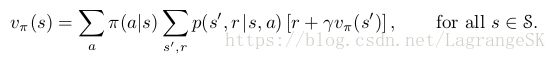强化学习系列（十一）：Off-policy Methods with Approximation

一、前言

针对Policy iteration 中存在的exploitation问题，在第五章中将强化学习算法分为on-policy算法和off-policy算法。前两章中，我们讨论了对on-policy问题的函数逼近，本章中将重点介绍off-policy问题的函数逼近。两者差异很大。第六章、第七章中出现的 tabular off-policy 方法很容易用semi-gradient方法进行扩展，但在off-policy下算法的收敛性比on-policy下差。本章我们研究收敛问题，加深对线性逼近的了解，介绍 learnable的概念，然后介绍一个对 off-policy而言，收敛性强的新算法。

回忆在off-policy learning 中，我们需要用behavior policy b b 生成的数据来学习target policy π π 的value function。在prediction 问题中，两个policy都是给定且不变的，我们需要找到特定的state value v̂ ≈vπ v ^ ≈ v π 或action value q̂ ≈qπ q ^ ≈ q π 。在control 问题中，要学习action value，两个policy在学习过程中都是变化的—— π π 是 q̂  q ^ 的greedy policy ， b b 则是另外一些探索性比较强的策略如 q̂  q ^ 的 ϵ ϵ -greedy policy。

off-policy learning 的挑战分为两大类：一类出现在表格化问题（tabular case) 中，与update target有关,另一类出现在函数逼近中，与update distribution有关。第5章和第7章中介绍的方法解决了第一类问题，本章第一节将探讨这些方法与函数逼近的结合。

但off-policy learning的函数逼近相比on-policy learning 需要一些其他东西，因为其中的update distrbution不再是on-policy distribution。on-policy distribution 起到了平衡对semi-gradinet的作用，在off-policy learning中，有两个方法可以用于解决该问题：

• 一个是第5章和第7章中介绍的importance sampling，此处将update distribution变为 on-policy distribution,保证了算法的收敛性。
• 另个一是开发一种不依赖于任何特定分布的 true gradient f方法。

二、Semi-gradient Methods

首先，我们开始讨论前几章中提到的off-policy 方法与函数逼近如semi-gradient方法的结合。这些方法重点针对 off-policy的第一类挑战，（不断变化的update targets)，而非针对第二类挑战（不断变化的update distribution），因此，对某些任务而言，这些方法会发散，但很多情况下表现良好。对tabular case是函数逼近的特例，使用这些方法可以确保稳定且无偏。所以可以用合适的特征选择方法，将两者结合起来得到一个稳定的系统。

在第7章中，我们讨论了很多 tabular off-policy 算法，将他们与semi-gradient算法结合，可以将更新（V 或 Q)变为用value function的逼近（ v̂  v ^ 或 q̂  q ^ )的梯度来更新（ w w )。这些算法大部分都采用了per-step importance sampling ratio:

---

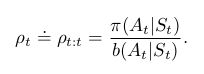
one-step state-value 算法 semi-gradient off-policy TD(0)：

其中：
episodic and discounted problem:

continuing and undiscounted problem:

---

action values, the one-step algorithm is semi-gradient Expected Sarsa:

---

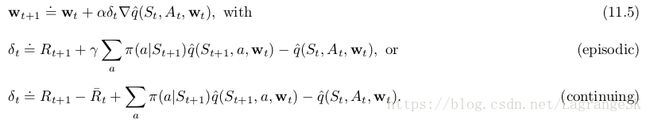
注意，这里并没有使用importance sampling。在tabular case中，很明显不需要用importance sampling，因为只有一个sample action At A t ，在学习这个action value 时，不需要考虑到其他的action。对函数逼近问题而言，不太明显，因为在进行一个全局逼近时，我们可能希望不同的state-action pairs有不同的权重。等我们更深入理解强化学习函数逼近思想时再说明更合适的处理方式，。

对muti-step 算法的泛化，无论是state value 还是 action value都需要importance sampling。

---

the n-step version of semi-gradient Expected Sarsa：

---

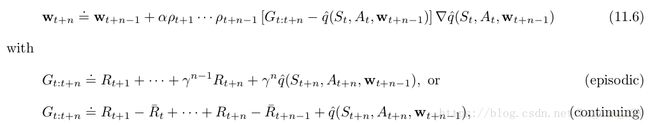
回忆第7章中不使用 importance sampling的off-policy 算法：n-step tree-backup算法。

---

the n-step version of semi-gradient tree-backup:

---

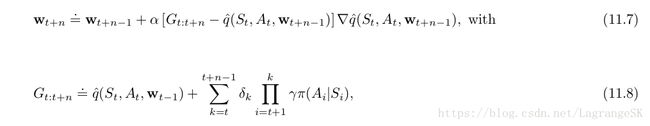
三、Examples of Off-policy Divergence

本节我们开始讨论使用函数逼近的 off-policy learning 的第二类挑战。这里的update distribution 不再满足 on-policy distribution。我们先来看一些使用 semi-gradient 或其他算法导致不稳定或不收敛的off-policy learning 反例。

先来看一个简单的例子。假设在一个大型MDP中，有两个states的估计 value function 是w 和2w的函数如下图，此处的参数矩阵 w w 仅仅包含一个量 w。本例中，特征向量值分别为1和2。在first state处，只有一个可行的action，执行这个action就一定会以reward为0转移到 second state。

假设初始时刻 w=10 w = 10 ，从estimated value为10的state转移到estimated value为20的state。看起来似乎是一个不错的转移，w会增加，first state 的estimate value会随之增加。如果 γ γ 接近1，那么TD error接近10，如果 α=0.1 α = 0.1 ，那么w以减小TD error为目标，会增加到接近11。second state的estimate value也会增加，接近22。如果再次转移，那么将从 ≈11 ≈ 11 的state转移到 ≈22 ≈ 22 的state，TD error ≈11 ≈ 11 ——比第一次转移大。first state 的value会再次增加到 ≈12.1 ≈ 12.1 。这样循环往复 w w 会增加到无穷大。

为了详细说明发生了什么，我们来看一下数学表达。TD error为：

off-policy semi-gradient TD(0)的更新为：

注意，本例中的 ρt ρ t 为1，因为在first state只有一个action，所以target 和 behavior policy下选择action的概率都是1。更新后的权重是更新前的 (1+α(2γ−1)) ( 1 + α ( 2 γ − 1 ) ) ，如果该值大于1，那么系统将不稳定，w会发散于无穷大。此处，当 γ>0.5 γ > 0.5 时，该值大于1。这表明系统是否稳定不依赖于step size（ α>0 α > 0 )，step size的大小只能影响w趋于正无穷的速度，不会影响w是否收敛。

这个例子的关键在于一直在重复一个状态转移下更新 w。这在off-policy learning 下是可能发生的，因为 behavior policy可能会选择target policy永远不会选择的那些 action。对于这些转移而言， ρt ρ t 可能为0，且这些转移上的权重不会更新。在 on-policy training中， ρt ρ t 总是1，那么从estimated value为10的state转移到estimated value为20的state会提升 w,则一定会有2w state之外的状态转移，这个转移会减小w。在on-policy中，future reward 会被传承下去，且系统会进行检查，但在off-policy中，future reward 虽然也可能被传承下去，但一旦选择action 后，future reward可能被遗忘了（ ρt=0 ρ t = 0 ）。

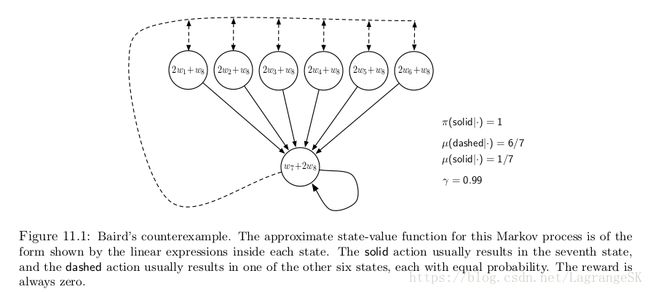
这个简单的例子说明了off-policy training为什么会发散的一些原因，但并不完整。因为他只是MDP中的一部分，会存在完全不稳定的系统吗？举个完全发散的例子——Baird’s counterexample。考虑一个有七个states，两个action的episodic问题，如图11.1所示。

虚线的action等可能的将state带向上面6个states，而实线的action 将state带向第7个state，behavior policy b选择虚线或实线的概率分别为 67 6 7 和 17 1 7 ，是均匀分布。target policy π π 则总是选择 实线action，也就是说 on-policy distribution 只能到第7个state，所有的状态转移reward 均为0，dicount rate γ=0.99 γ = 0.99 。

state-value的线性估计表示在圆圈内部。例如，最左侧的state estimated value为 2w1+w8 2 w 1 + w 8 ,对应的特征向量为 x(1)=(2,0,0,0,0,0,0,1)T x ( 1 ) = ( 2 , 0 , 0 , 0 , 0 , 0 , 0 , 1 ) T ，由于所有的状态转移reward 均为0，所以所有state s 的true value function vπ(s)=0 v π ( s ) = 0 ，当 w=0 w = 0 时被准确估计。 事实上，很多问题中，权重向量的维度（8维度）大于 state的维度（7维度)。这也就是说 {x(s):s∈S} { x ( s ) : s ∈ S } 是线性独立的。这个例子比较像我们用线性函数逼近时遇到的一般情况。

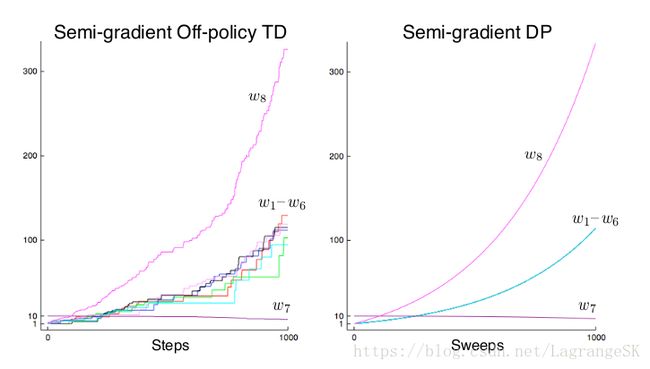
如果，我们此时采用 semi-gradient TD(0)，那么权重会发散到无穷大。无论采用多大的正向 step size都会发散。如果采用DP形式更新：

也会发散。

如果我们将Baird’s counterexample中的DP update distribution变成 on-policy distribution，模型会收敛。TD 和DP方法是最简单易懂的bootstrapping方法，线性semi-gradient是最简单的函数逼近方法，这两者在update distribution 不满足 on-policy distribution情况下的结合都会导致算法不稳定。

还有一个与 Baird’s counterexample类似的 counterexample表示了使用Q-learning的发散，这值得我们注意，因为Q-learning是收敛性最好的control 方法。考虑如何补救的思路一般是使得behavior policy 和target policy足够接近，如 ϵ ϵ -greedy policy。接下来，我们介绍另外一些思想。

假设和 Baird’s counterexample不同，不再是每次迭代都朝着 expected one-step return 前进一步，现在以最小均方根误差为标准来改变 value function。这会改善不稳定问题吗？当 {x(s):s∈S} { x ( s ) : s ∈ S } 线性独立时（如 Baird’s counterexample中）当然可以。因为每次迭代都会使得准确度上升，使得tabular DP的平均值下降。但这个例子中，即使这么处理了，还是不能保证系统稳定，如图所示：

另一种防止系统不稳定的方法是采用特殊的函数逼近方法，尤其是不用observed target进行预测的函数逼近方法，这些方法被称为 averages,包括最近邻方法和locally weighted regression，但不包括 tile coding 和 artificial neural network。

四、The Deadly Triad

上一小节中，我们举例说明了系统存在不稳定性的情况，本节对系统不稳定性情况进行整体归纳分析。可能导致系统不稳定的元素有三——死亡三元素：
Function Approximation（函数逼近）、Bootstrapping 和off-policy training，当三者同时出现时，会导致系统不稳定，而只出现其中两个时，系统会稳定，那么如何取舍？

首先，function approximation不能被舍弃，我们需要用他来泛化强化学习方法，扩展强化学习的应用，至少需要一个线性函数逼近。 State aggregation(聚类）或非参数化的方法随着数据增加复杂度增加，且效果不是太强就是不足，Least-square 方法如LSTD的计算复杂度太高。

不用 bootstrapping是可以的，但是要牺牲计算效率和数据利用率。首先来看计算效率，MC方法需要记忆库来存储每次预测和最终返回值间的所有信息，当获得最终返回值时，完成所有运算，对计算机硬件要求高。在bootstrapping和 eligibility trace(第12章会谈到）中，数据都是用完就丢弃的，不需要很多存储空间。

不用bootstrapping的数据利用率损失也是不可忽略的，在第7章和第9章中的random-walk例子中，一些 bootstrapping方法表现比MC方法好。实验结果表明 bootstrapping方法的学习速度更快，原因在于他可以利用最终返回值之前的states特性来进行学习。但bootstrapping在state没有明确表达的问题（仅仅知道特征向量的情况）中表现不好，会导致一些不好的泛化。总体来说，boostrapping方法是很有价值的，但可以选择用 n-step updates来取代单步更新。

最后，我们来看 off-policy learning，我们可以放弃吗？On-policy方法通常情况下足够强大。对 model-free 强化学习问题来说，我们可以使用Sarsa而不是 Q-learning。off-policy 方法将target policy和behavior policy区别开来，会使得运用变得简单，但不是必须的。但 off-policy learning 对一类预测问题来说十分有效，这类问题书中没有提到，但对构建更有智慧的高级智能体来说十分重要。

在这类问题中，agent 不仅学习一个value function和单个policy，而是要并行学习一系列的 value function和Policy。这基于人和动物的可以通过学习来预测不同事件（不仅仅是预测reward）的普遍真理。我们对不寻常的事件表示惊讶，然后会更正我们对事物的预测，无论往好预测还是往坏预测。这种预测假设是规划中预测模型的基础。我们根据眼睛看到的场景进行预测，如估计需要多长时间走回家，打篮球时篮球跳起的可能性，对新接收项目的满意度。这些任务中，需要预测的事件和我们的行为密切相关。如何并行的学习他们？需要从一部分经验中学习，此时有很多target policy，一个behavior policy不可能平等的对待他们，并行学习的behavior policy 可以部分重叠这些target policies，为了并行学习，需要使用 off-policy learning。

五、Linear Value-function Geometry

为了更好的理解 off-policy learning 所面临的稳定性挑战，将value function approximation 独立与learning 之外，进行抽象分析。假设一个state space中的所有state-value function 都是实数 v:S→R v : S → R ，且大部分value function 不对应任何 policy。我们的目标不再是找到一个可以用的函数逼近，而是找到一个参数小于states个数的函数逼近。

假设有一个state space S=s1,s2,...,s|S| S = s 1 , s 2 , . . . , s | S | ，任何value function v v 都相当于一个由每个state value以此组成的矢量（vector) 列表 [v(s1),v(s2),...,v(s|s|)]T [ v ( s 1 ) , v ( s 2 ) , . . . , v ( s | s | ) ] T ，这个关于value function的 vector representation 和state的元素个数相同。在我们想要使用函数逼近的大多数情况下，元素太多不利于 vector的明确表达。但这种vector的思想在概念上很有用，下文中，我们交替使用 value function 和他的vector representation。

假设有一个任务，有三个states S=s1,s2,s3 S = s 1 , s 2 , s 3 ，两个参数 w=(w1,w2)T w = ( w 1 , w 2 ) T ，我们认为所有的value function/vectors都是一个三维空间（space) 中的点，参数在一个二维子空间（subspace)中提供了代替坐标系。任意权重向量 w=(w1,w2)T w = ( w 1 , w 2 ) T 是二维子空间中的点，因此一个完整的 vw v w 与每个state均有关。在一般函数逼近问题中，full space和 subspace的关系比较复杂。但本问题中，使用线性函数逼近，因此subspace是一个简单平面，如图11.3所示。

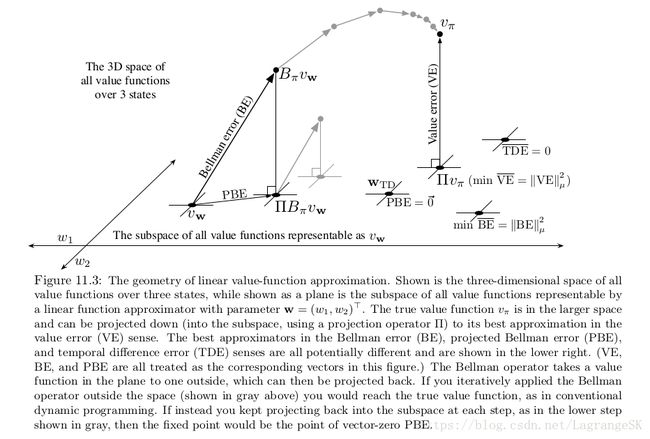
对一个给定 policy π π 而言，我们假设 true value function 为 vπ v π 很复杂，以致于不能被函数逼近准确表示。因此， vπ v π 不在subspace中，在图中，表示为高于subspace平面。

如果 vπ v π 不能被准确表示，那么如何表达可以更接近？有很多方法。首先，我们需要知道如何测量两个 value function 之间的距离。假设 有两个value function v1 v 1 和 v2 v 2 ，向量差为 v=v1−v2 v = v 1 − v 2 ，如果v很小，那么这两个value function很接近，但我们如何测量这个向量差的大小？因为我们对每个state的关注度不同，我们会觉得出现更频繁的state比其他state重要，所以传统欧几里得距离不太适合计算这个向量差。在第九章第三节中我们用分布 μ:S→[0,1] μ : S → [ 0 , 1 ] 来量化对不同state的关注度，我们可以定义两个value function之间的距离如下：

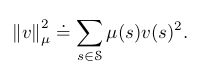
第九章第三节中的 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 可以写作 VE⎯⎯⎯⎯⎯⎯⎯⎯=||vw−vπ||2μ V E ¯ = | | v w − v π | | μ 2 。对任何 value function v, 在subspace of representable value function上寻找最近的value function是一个投影操作(project operator)。我们将任意 value function 投影到 representable function 上的投影运算定义为 Π Π :

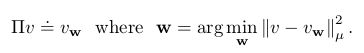
最接近true value function vπ v π 的representable value function叫做 投影 Πvπ Π v π ，如图11.3所示。这是MC算法中常用求解方法，虽然很慢。关于投影运算在阴影box中进行详细讨论。

TD方法采用不同的求解方法，从Bellman等式得到启发。

如果用函数逼近得到的 vw v w 代替 vπ v π ，则左右两侧不再相等，有一定差值，这个差值就是 Bellman error ：

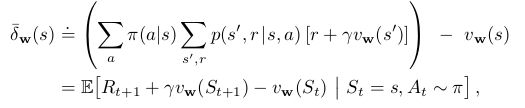
观察发现，Bellman error是TD error的期望值。

所有state的Bellman error组成了Bellman error vector（图11.3中用BE表示），定义Mean Squared Bellman Error如下：

不可能将 overlineBE o v e r l i n e B E 减小到0（此时 vw=vπ v w = v π )，但对线性函数逼近而言，有特定的 w w 使得 overlineBE o v e r l i n e B E 最小，如何最小化 overlineBE o v e r l i n e B E 将在接下来的两章中讨论。

为了简化表达，在图11.3中Bellman operator 记作 Bπ B π :

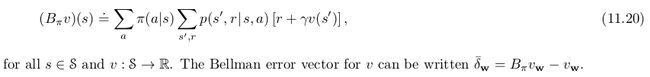
如果在representable subspace上对 value function用 Bellman operator ，通常会产生在subspace 平面之外的新的value function。在不加函数逼近的DP中，如图11.3灰色箭头所示，反复用Bellman operator ，最终会收敛到true value function vπ v π 上，对Bellman operator 而言只有一个 fixed point ,此时

对函数逼近而言，中间的value function（在subspace之外）无法表示，图11.3上灰色箭头无法依次执行，因为在一次更新后（dark line）value function会再次投影到 representable space，下次迭代从subspace开始。循环往复，是一个类似DP的过程。

这里，我们重点关注从Bellman error vector到representable suspace的过程。定义一个projected Bellman error vector Πδ⎯⎯⎯vw Π δ ¯ v w ，在图11.3中为PBE。对任意逼近获得的value function，定义 Mean Square Projected Bellman Error ( PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ )：

对线性函数逼近，总有一个使得 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 为0的approximate value function（ within subspace)，对应TD fixed pointed wTD w T D ，这个点在semi-TD方法和 off-policy来说，不是很稳定。如图11.3所示，用 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 得到的value function和通过最小化 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 或 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 得到的value function 明显不同。在第8节和第9节讨论一定会收敛的方法。

六、Stochastic Gradient Descent in the Bellman Error

为了更好的理解value function approximation和 various objectives（迄今，我们介绍了 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 、 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 和 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 等 目标函数），我们回到 off-policy learning所面临的稳定性挑战上。

在最小化这些目标函数时，一般会采用SGD(随机梯度下降法），但在已经介绍过的方法中，只有MC采用了真正的SGD。这种方法on-policy和off-policy上的非线性函数逼近的收敛鲁棒性很好，但收敛速度比不上 semi-gradient with bootstrapping方法。但semi-gradient方法在off-policy training时可能会发散，且不适用与非线性函数逼近。但true SGD方法不存在这样的问题。

本节和下一节我们将Bellman error作为SGD的目标优化函数进行研究，虽然这是一个有趣的方法，但不是一个好的学习算法。

首先，考虑一个简单的问题，时间差分方法是TD error 驱动的，那么为什么不直接将 TD error的期望平方作为优化目标？在一般函数逼近问题中，one-step TD error with discounting如下：

我们可以将 Mean Squared TD Error作为目标函数：

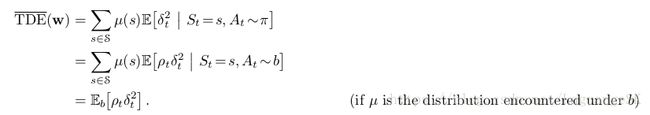
最后一个等式是SGD所需要的，提供了可以从经验中采样的期望目标函数。（经验有behavior policy b得到，因此，SGD权重更新如下：

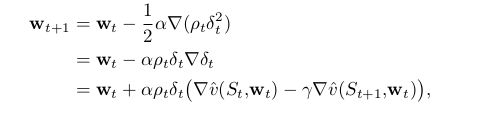
（semi-gradient TD）
除了最后一项外和semi-gradient TD算法的更新公式一样，这一项使得该算法为一个完整的gradient ，构成了可以收敛的true SGD方法，我们称该方法为 naive residual-gradient 方法。

虽然 naive residual-gradient 方法的收敛鲁棒性不错，但不会收敛到理想值。我们用一个A-split例子进行说明。本例中采用 tabular 表示，因此可以直接表示出 true state values,但naive residual-gradient 方法找到的是不同的value，这些value的 overlineTDE o v e r l i n e T D E 比true value的小。最小化 overlineTDE o v e r l i n e T D E 太过理想，对所有 TD error进行处罚更像在进行差分平滑，而不是寻找精确预测。

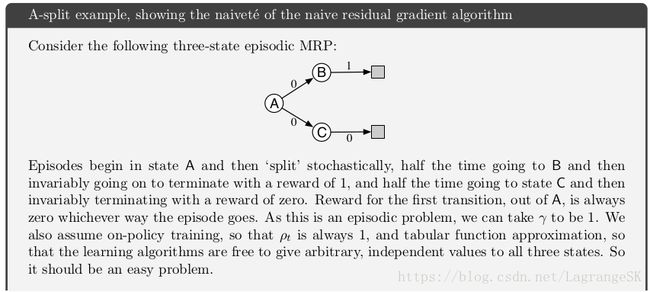
更好的想法是最小化 Bellman error。如果学到精确的value，那么Bellman error 处处为0。因此，Bellman-error-minimizing算法用于A-split例子没问题。但我们不应该期望可以找到使得Bellman error处处为0的解，这意味着value的精确解，我们假设这个精确解在representable space之外。但可以以这个解的近似解作为求解目标。我们已经知道Bellman error是TD error的期望，权重更新公式如下：

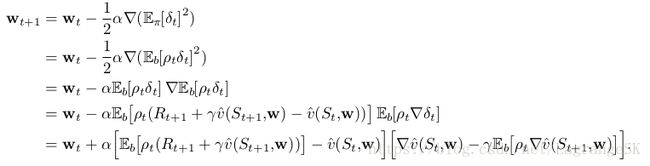
这种算法被称为residual gradient algorithm。为了获得无偏差采样，需要对next state进行两次独立采样，但在与环境正常交互过程中只能得到一次采样。无法同时获得两次采样。

有两种方法可以使得residual gradient algorithm有效，一个方法是基于确定性环境，如果从一个state到另一个state的转移的确定性的，那么两次采样结果的等同的。另一个方法是获得从 St S t 到 St+1 S t + 1 的两个独立采样。在与环境真实交互过程中，看起来不可能实现第二种方法，但和一个仿真环境进行交互时可以。在前进到first next state之前，简单回到之前的previous state然后获得一个 alternate next state。无论采取哪种方法的residual gradient algorithm都是一种true SGD方法，对线性和非线性函数逼近的鲁棒性都很强，在线性函数逼近中，有唯一解。

但，residual gradient algorithm的收敛性至少在这三方面不能令人满意：

• 比semi-Gradient算法慢
• 可能收敛到错误value。在所有tabular cases中都收敛到正确值，如A-split 例子，但对于涉及到函数逼近的例子，residual gradient algorithm可能会收敛到错误的value,如下框图所示。这个例子表示最小化 overlineBE o v e r l i n e B E 不一定是一个理想目标。
• 收敛性不能完全保证，下一节详细说明。

七、The Bellman Error is Not Learnable

本节所介绍的可学习性概念不同于机器学习中的概念。通常，如果我们说一个方法“learnable”，则表示在多项式计算复杂度下可以有效学习而不是在指数复杂度下。对强化学习问题而言，我们用一种更基本的方式定义“learnable”，基于大量经验数据而言。但大部分强化学习方法在无限多经验数据下不能收敛。这些方法通常可以在已知环境信息下进行运算，但不能从已观测到的特征向量（feature vector)、action和reward序列中进行计算或估计。这种称为 not learnable。很不幸，本节将说明Bellman Error objective 方法是 not learnable的。

为了明晰概念，我们先看一些简单的例子，有如下两个MRP（Markov reward processes）图：

假设每种转移都是等概率的，线上数字表示reward。所有states均相同，由特征向量x=1 和权重w构成。因此，reward是引起data trajectory变化的唯一因素。左边 MRP表示只有一个状态会随机获得0或2的reward（概率均为0.5）。右图MRP,每一步从state到另一个state是等可能的，因此，即使给了无穷多的数据，也无法判断是由哪个MRP产生的。

这组MRP也表明了 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 的不可学习性。如果 γ=0 γ = 0 ，三个state 的true value 从左到右依次是1,0,2，假设 w = 1。那么left MRP的 VE⎯⎯⎯⎯⎯⎯⎯⎯=0 V E ¯ = 0 ，right MRP的 VE⎯⎯⎯⎯⎯⎯⎯⎯=1 V E ¯ = 1 ，虽然有相同的data distribution，但 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 值不同，这表示 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ not learnable。那么 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 是否适合作为学习目标呢？

一般来说，如果一个目标函数not learnable，那么他自身有问题，但 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 是个例外。注意对上面两个MRP而言， w=1 w = 1 。这是一种巧合吗？有相同分布的 MDP的最优参数向量相同吗？答案是肯定的，后面会讲到为什么。那么 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 还是一个可用的目标函数，虽然他not learnable，但还是可以用 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 来优化参数。

为了更好的理解这个情况，我们介绍一个肯定learnable的natual objective function，即value估计值和return之间的误差，Mean Square Return Error( RE⎯⎯⎯⎯⎯⎯⎯ R E ¯ )，在on-policy中可以写作

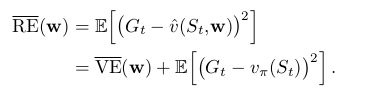
除了 E[(Gt−vπ(St))2] E [ ( G t − v π ( S t ) ) 2 ] 外， RE⎯⎯⎯⎯⎯⎯⎯ R E ¯ 和 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 一样，但 E[(Gt−vπ(St))2] E [ ( G t − v π ( S t ) ) 2 ] 这一项与权重 w w 无关，因此，可以说 RE⎯⎯⎯⎯⎯⎯⎯ R E ¯ 和 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 对应的optimal parameter value w∗ w ∗ 是相同的，如下图。而 RE⎯⎯⎯⎯⎯⎯⎯ R E ¯ 又是可学习的，因此可以求出optimal parameter value w∗ w ∗ ，因此 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 的参数是可以优化的。

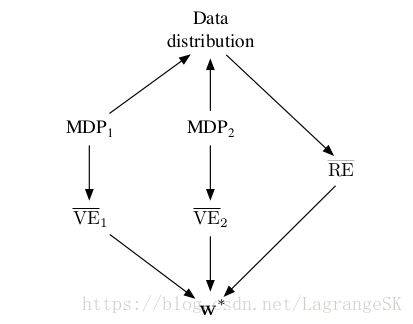
现在回到 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ ， BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 和 VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ 一样，可以由MDP信息中计算但无法根据经验数据进行学习（not learnable)，但不同的是，对 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 最小化求解的方法是不可用的。阴影框图（p226,此不详述) 中的例子说明了这个问题——有两个产生相同data distribution的MRP,但两者最小化参数向量不同，证明了optimal parameter vector不是关于 data的函数，因此不可以根据data学习到。

另外两种bootstrapping的方法， PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 和 TDE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ T D E ¯ 都是由data直接决定的（learnable)，但求得的optimal parameter vector均不同，如图所示。

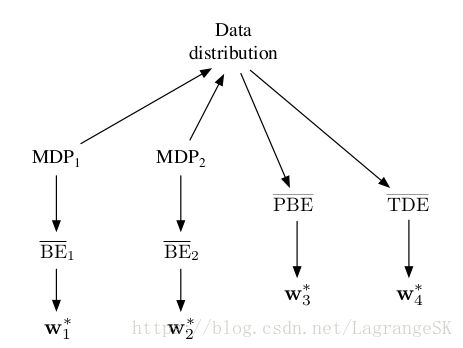
因此， BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 是not learnable的，不能由特征向量和其他可观测数据估计得到。这使得 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 只能用于model-based setting，没有算法可以在不使用MDP state(而不是特征向量）的前提下最小化 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 。residual-gradient算法是唯一可以最小化 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 的方法，通过对same state（not a state that has the same feature vector) 进行二次采样。最小化 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 必须依赖 MDP环境信息，因此，该方法局限性较高，我们现在重点关注 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 。

八、Gradient-TD Methods

我们现在考虑最小化 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 的SGD方法，对true SGD methods而言，gradient TD methods对off-policy tarining 和 non-linear function收敛鲁棒性较强。记得在线性逼近中，总有一个TD fixed point wTD w T D ，使得 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 为0。可以用least–square方法找到这个解，但计算复杂度为 O(d2) O ( d 2 ) ，我们想找到计算复杂度为 O(d) O ( d ) 且收敛鲁棒性强的SGD方法。Gradient TD方法满足这些条件。下面我们介绍如何推导这个方法。

首先，用矩阵形式表示 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ ，

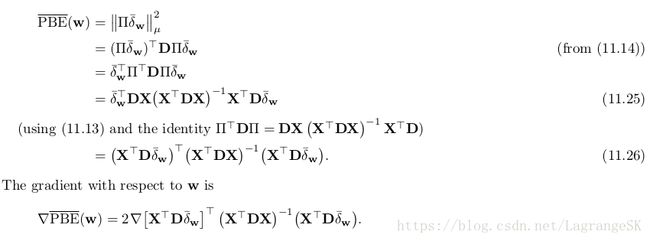
μ μ 是由behavior policy生成的state的distribution，上式三个部分都可以表示为该分布下的期望。

我们从未将梯度表达式写成这样的形式：三者乘机，且第一项和第三项不相互独立，都依赖于下一时刻的特征向量 xt+1 x t + 1 ,我们无法通过简单采样计算出每个期望，然后相乘。这会和naive residula-gradient算法一样，产生梯度的有偏估计。

另一种思路是分开估计这三个期望，然后组合来产生梯度的无偏估计。这是可行的，但需要很多计算资源来存储期望值，尤其对前两项 dxd的期望矩阵来说，还需要计算第二个矩阵的转置。进一步改善这样想法，如果其中两项被估计和存储，那么第三项可以通过采样获得。例如，可以估计后两项，采样得到第一项。但不幸的是，这种计算方式的计算复杂度仍然为 O(d2) O ( d 2 ) 。

这种思想在gradient TD中也会用到，gradient TD估计并存储前两项计算相乘的结果，第一项和第二项维度分别为dxd 和 d维，故相乘结果为d维向量，将此记为 v:

这种形式和linear supervised learning很像，试图从特征中估计 ρtδt ρ t δ t 的linear least-square 问题解法。传统SGD方法以最小化期望方差 (vTxt−ρtδt)2 ( v T x t − ρ t δ t ) 2 （Least Mean Square,LMS）为目标通过迭代方式更新 v v :

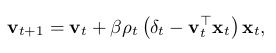
其中 β>0 β > 0 是另一个step-size参数，这使得我们每次存储和计算复杂度降低为 O(d) O ( d ) 。

当给定一个 vt v t 时，我们可以用SGD方法更新TD：

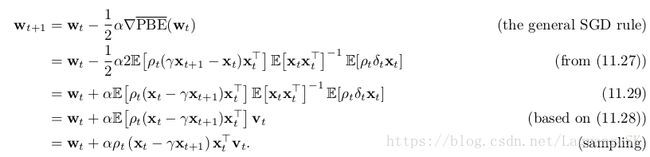
这个方法叫做 GTD2。如果先求出 (xTtvt) ( x t T v t ) ，那么整个算法的计算复杂度为 O(d) O ( d ) 。
更好的算法是在计算 vt v t 前进行一些分析，从（11.29）开始：

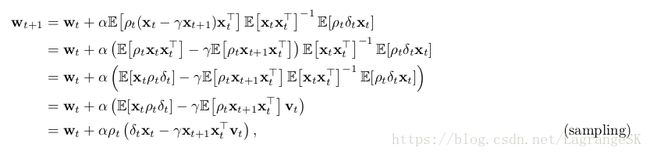
如果先求出 (xTtvt) ( x t T v t ) ，那么整个算法的计算复杂度为 O(d) O ( d ) 。这种算法被称为TD(0) with gradient correction(TDC)或 GTD（0）。

GTD2和TDC都包括两个学习过程，主学习过程学习 w w ，次学习过程学习 v v ，次学习过程需要在主学习过程之前完成，这种依赖关系被称为层叠（cascade），在层叠中我们常假设次学习过程学习的快，且有一个渐进值，可以用于主学习过程，这些方法的收敛性证明（被称为 two-time-scale证明）使得这些假设成立。fast time scale是次学习过程， slower time scale是主学习过程，如果 γ γ 是主学习过程的学习率， β β 是次学习过程的学习率，则需要满足 limβ→0 l i m β → 0 且 αβ→0 α β → 0 。

Gradient- TD方法是最为简单易懂且应用广泛的stable off-policy 方法。有很多衍生方法，参考书中（P229)。

九、Emphatic-TD Methods

我们现在来看另一种更为高效的采用function approximation的off-policy learning method。回忆在on-policy distribution 中，线性semi-gradient TD 方法高效且稳定。在第9章第5节中表明，该方法必须有一个正定矩阵 A A ，以及在target policy下有一个 和on-policy state distribution μπ μ π 对应的状态转移概率 p(s|s,a) p ( s | s , a ) 。在off-policy learning 中，我们对状态转移概率进行了importance sampling使之适用于target policy的学习，但state distribution 仍然由behavior policy生成，这会导致错误匹配。很自然想到如果对states重新分配权重，强调其中一些state弱化另一些state，使得update distribution变成 on-policy distribution。这就是Emphatic-TD method的思想，在9.12中介绍过。

事实上，“the on-policy distribution”这个词不太准确，因为有很多 on-policy distribution，任何一个都可以保持稳定。考虑一个undiscounted episodic problem，episode 的结束方式完全取决于状态转移概率，但每个episode的起点可能不一样。但是无论episode起点在哪，如果所有的状态转移概率均由target policy产生，那么state distribution就是 on-policy distribution。可能会从接近terminal state的地方作为起点，然后在episode结束之前只经过几个出现概率高的states。也可能会从远离terminal state的state开始一个episode。这两者都是 on-policy distribution，用linear semi-gradient 方法进行训练都会稳定收敛。无论怎么开始，只要所有的states都被遍历且在结束前更新过，那么on-policy distribution总会有结果。

如果是discounting，可以被看做上述情况的partial or probabilistic termination。当 γ=0.9 γ = 0.9 ，那么我们认为每个time step有0.1的概率程序终止，然后立刻在刚刚转移的state处复活。discounted 问题在每一步都有 1−γ 1 − γ 的概率持续终止又复活。这种看待discounted 问题方式是“伪终止”（pseudo terminal）的一种，“伪终止”并不因为终止而影响状态转移序列，但会影响学习过程和学习质量。这种“伪终止”对off-policy learning 很重要，因为复活是可以选择的——我们可以选择任意我们喜欢的state开始复活——终止减轻了on-policy distribution中不断经过state的需求。因此，如果我们不考虑在新的state处进行复活，那么discounting可以快速生成一个limited on-policy distribution。

用以学习episode states value的one-step emphatic-TD 算法定义为：

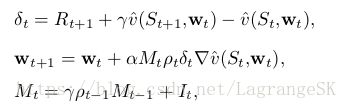
其中， It I t 表示 interest，是随机值， Mt M t 表示 emphasis,初始值为 Mt−1=0 M t − 1 = 0 ，该算法对Baird’s counterexample性能如何？

Figure 11.7 shows the trajectory in expectation of the components of the parameter vector (for the case in which It I t = 1, for all t). There are some oscillations but eventually everything converges and the VE⎯⎯⎯⎯⎯⎯⎯⎯ V E ¯ goes to zero.

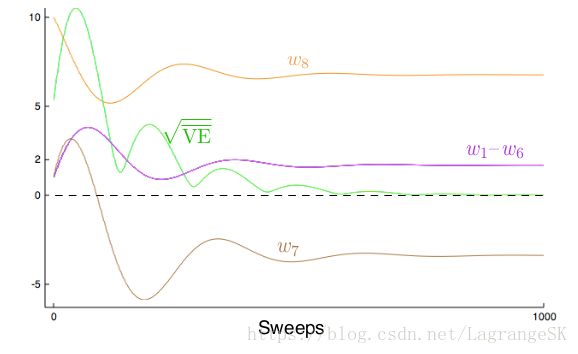
These trajectories are obtained by iteratively computing the expectation of the parameter vector trajectory without any of the variance due to sampling of transitions and rewards. We do not show the results of applying the emphatic -TD algorithm directly because its variance on Baird’s counterexample is so high that it is nigh impossible to get consistent results in computational experiments. The algorithm converges to the optimal solution in theory on this problem, but in practice it does not. We turn to the topic of reducing the variance of all these algorithms in the next section.

(总结，该算法方差较大，下一节讨论如何减小这类方法的方差）

十、Reducing Variance

书上有很多参考文献，此不详述

十一、总结

设计出一个平稳且高效的学习算法对off-policy learning来说挑战性很高。Tabular Q-learning 算法使得off-policy learning看起来很容易，这种算法泛化表示有 Expected Sarsa 和 Tree Backup算法。但在本章中可以看出，针对函数逼近问题，即使是最简单的线性函数逼近，这些算法都无法很好的扩展，off-policy learning 都面临着新的挑战，需要我们进一步理解强化学习算法。

既然这么复杂，为什么要将函数逼近用于 off-policy learning 呢？只用在 on-policy learning中不行吗？这就要说到 off-policy 的两大优点：可以平衡exploration和exploritation;将数据生成和学习过程区分开，防止了target policy的专制。TD learning使得同时学习很多东西成为可能，可以用一个经历来同时对应很多任务。

本章中将off-policy learning分为两部分来讨论。第一部分针对off-policy learning 中不断变化的update target，针对tabular case，在第5章到第7章中提供了一些解决方案（off-policy TD 等），但存在很大的方差，这也是off-policy learning 的一大挑战。

第二部分是本章关注的重点，主要发生在将函数逼近用于 off-policy learning时。我们发现一旦集齐 function approximation，off-policy learning 和bootstrapping TD method三大死亡要素，算法必然发散。那么很自然想到去掉其中之一，这里我们考虑去掉bootstrapping TD method。有很多处理方案。最受欢迎的是找到一个基于Bellman error BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 的true SGD方法。但本章中我们分析该方法由于 BE⎯⎯⎯⎯⎯⎯⎯ B E ¯ 是 not learnable的，因此在很多情况下不适用。另一个方案是，Gradient-TD methods，将SGD用于projected Bellman error PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 。 PBE⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ P B E ¯ 是一个learnable的计算复杂度为 O(d) O ( d ) 的目标函数。（but at the cost of the second parameter vector with a second step size.)最新的方法是 Emphatic-TD方法，有侧重的进行更新，基于这一思想，在off-policy learning中采用semi-gradient方法的同时保留了on-policy learning的稳定性。

《Reinforcement Learning:an introduction》 by Sutton and Barto