北航OJ-2014级第2次算法上机题解
北航OJ-2014级第2次算法上机题解
A.零崎的补番计划Ⅰ
题目描述
零崎是个很喜欢逛b站的人,除了Korea相关和哲♂学,零崎什么都看。b站每天都有好多up主更新视频,零崎自然不可能每个视频都看,而且零崎平时在学校又忙着各种各样的社(da)团(ma)活(jiang)动,所以零崎一贯在放假的时候补番。
一般来说,零崎会按照b站的评分挑选出最大的k个来补,不过零崎倒也不在意最终补番的顺序,所以你们只要把第k大的评分找出来,之后零崎自己去选出所有比第k个大的就可以了。
输入
多组测试数据。 对于每组数据,第一行为两个整数n与k,表示有n个视频,零崎要补k部番(1<=k<=n<=1000000)。假定评分均不相同。
第二行包含n个整数,用空格隔开,为各种各样的评分。## 输出 对于每组数据,输出一个整数,为排名k的视频的分数。
输入样例
5 3
1 3 4 2 5
5 1
5 7 6 8 2
输出样例
3
8
Hint
这是一个排序,这又不是一个排序。
解题思路:
这题考查的算法是第i顺序量查找。
但是和CLRS上的算法有所不同的是,这题要求查找的是从大到小的第i个量。解决方法有两种:
(1) 改写partion函数,使其变成能够直接返回从大到小的第i个量的方法;
(2)换种思路,对于一个长度为n的数组,第i个值最大的值,就是最小的第n-i个值。(很明显这种方法更简单啦~~)。
直观感受一下 (A[n]是一个升序排列好的数组):
解题代码:
#include if(A[j]<=x)//加上=号很重要,为了把相等于主元(即A[q])的元素全部都集中到中部
swap(A[++i], A[j]);
}
swap(A[++i], A[high]);
return i;
}
//把A[i]归位
int randomPartion(int A[], int low, int high)
{
int i = rand()%(high-low+1)+low;
swap(A[i], A[high]);
return partion(A,low,high);
}
//判断p
int randomSelect(int A[], int low, int high, int i)
{
if(low==high)
return A[low];
int temp = randomPartion(A, low, high);
int order = temp-low+1;
if(i==order)
return A[temp];
else if(ireturn randomSelect(A, low, temp-1, i);
else
return randomSelect(A, temp+1, high, i-order);
}
int A[1000001];
//对于所有的逻辑位置,输入的所有i的位置,我们默认为其中的物理位置
int main()
{
srand(time(NULL));
int n, k;
while(scanf("%d%d", &n,&k)!=EOF)
{
getchar();
for(int i = 0; iscanf("%d",&A[i]);
if(k>0 && k<=n)
printf("%d\n", randomSelect(A, 0, n-1, n-k+1));
}
} B.零崎的补番计划Ⅱ
题目描述
虽然零崎已经有了补番目录,然而零崎发现就算是假期,他也有各(da)种(ma)各(jiang)样的事情要做,所以零崎现在要在有限的时间内尽量补完更有价值看的视频。
零崎的假期一共有T时间,现在有k个视频,每个视频的价值为v,时间长度为t,零崎会好好看完不会随意快进。
输入
多组测试数据。
每组数据第一行为两个整数T和k,表示总时间和视频数量。
接下来k行,每行两个数据vi,ti代表第i个视频的价值和时长。
1<=T<=200000,1<=k<=300,1<=v,t<=200
输出
对于每组数据,输出一行,为零崎能看完的视频的价值总和的最大值。
输入样例
6 3
1 2
2 3
3 2
2 4
3 1
2 1
1 3
1 5
输出样例
5
5
解题思路:
这道题目考察0-1背包问题。
0-1 背包问题是一个DP问题,但是当时在学习它的时候,并没有像学习钢管切割问题一样很快就理解了。原因在于:钢管切割问题是一维的,也就是说动态变化的量仅仅是钢管的长度,只需要对于钢管长度进行DP求解就可以了;但是0-1背包问题则需要同时对于装入背包的物品个数以及背包容量这两个量进行二维的DP求解。
但是还是遵循DP的本质思路:利用状态转移方程,用保存下来的子问题的解构建规模更大的父问题的解,即“由小构大”。
我用我自己的语言叙述一下0-1背包问题的解决方法:
0-1背包问题: 已知背包最大容量W,以及N个物品的重量weight[]和价值value[],求如何装,才能使得背包所装物品的总价值最大。
先引入一个记号:maxVal[i][w]。maxVal[i][w]表示:用前i件物品填充容量w的背包,最终能得到的最大价值。比如maxVal[N][W]就是N个物品放入容量为W的背包里所能产生的最大价值,也就是本问题我们所需要的解。
如果我们已知maxVal[i-1][0], maxVal[i-1][1], maxVal[i-1][2], … , maxVal[i-1][W],那么我们可以利用这些子问题的解,求得maxVal[i][0], maxVal[i][1], maxVal[i][2], … , maxVal[i][W]。按照这种方式,我们通过不断增大i的值,也就是放入背包中的物品数,就可以得到maxVal[N][W]的值,也就是我们想要的的解了。
直观感受一下构造顺序:(表格里填写的是构建顺序的编号,其中对于物品数等于0,以及背包容量等于0的情况,初始化的时候全部设置为0,所以默认构建顺序全部为0):

状态转移方程为:

所以我们要做的就是:使用状态转移方程并且按照上图顺序,使用DP方法填表求解。
这是最基础的方法,但是空间复杂度太高,O(NW)级别,所以为了节省空间,我们可以优化这个问题的空间:只使用一个maxVal[W+1]的一维数组进行类似于上图的DP过程。关键之处就是:二维数组方法中,我们使用行来保存子问题的解,比如我们要求maxVal[i][W]的值,只需要调用保存下来的maxVal[i-1][]中的子问题的值就可以了。但是一维数组方法中,我们使用循环次数控制放入背包中物品的个数i,进行原地更新。
直观体会:
假设现在的数组maxVal[]存储的是把前i-1个物品放入容量为0,1,2,…,W的背包中,能获得的最大价值,即原二维数组的maxVal[i-1][0], maxVal[i-1][1], maxVal[i-1][2],…, maxVal[i-1][W]。
我们想要使用这些子问题的解,得到maxVal[i][0], maxVal[i][1], … , maxVal[i][W]的值。
现在以maxVal[k]为例,假设已经得到前i-1个物品放入背包的一系列子问题的解,现在要计算把前i个物品放入背包时的一系列解。
(1) 若weight[i]>W,表明物i无法放入背包,所以根据状态转移方程,我们有maxVal[k]的值保持不变。
(2) 若weight[i]<W,那么根据状态转移方程,我们要用到maxVal[k-weight[i]](现在的maxVal[k-weight[i]]里存储的值其实是就原来二维数组里的maxVal[i-1][k])用图解释大致就是如下的过程:
可见,要想更新某个值,必须使用其前面未经过更新的值!
我们看一下更新顺序对于更新的影响(黄色部分表示已经更新的值)
(1) 如果我们从右到左更新:

没关系,因为我们每次的更新不会覆盖左边的值,也就不会对之后的更新产生影响。(2) 我们对于maxVal[]进行从左到右的更新,就会对之后的更新过程产生影响:

此时的maxVal[k-weight[i]]已经不是maxVal[i-1][k-weight[i]]了,而是maxVal[i][k-weight[i]]!
所以对于这种更新方式,我们选择从右至左的更新思路。附上二维数组的背包代码,有助于理解背包问题:(会MLE哦~~)
#include 其实0-1背包问题里面,很关键的一个步骤就是:进行结果的抽象,就是说我们的dp[][]数组里面存储的值仅代表最大的价值,跟怎么装的完全没有关系。也就是说,下一个决策的做出,虽然要依赖于之前的决策结果,但是不会受到之前决策方案的影响。所以我们抽象着整个结果为dp[][]。
解题代码:
#include C.零崎的补番计划Ⅲ
题目描述
现在要补的番也确定了,不过还有个问题。
视频一口气看的太多,难免有些头疼,对于不同的看法,头疼程度自然也是不一样的。
对N个视频V1……Vn,如果任意两个视频i,j连续看有头疼程度e,则用矩阵A[i][j]=e表示。e=-1表示零崎不会连续看这两个视频。
那么零崎如果决定一次看完Vi和Vj最少的头疼程度是多少?(从Vi开始看到Vj结束)
输入
多组测试数据。每组测试数据第一行为两个整数N,Q,代表头疼矩阵的大小和查询次数。
接下来N行每行N个整数,为头疼矩阵。
最后Q行每行2个整数i,j为零崎要看的视频编号。
1<=N,i,j<=500,Q<=20,e<=100
输出
每组一个整数,为能找到的最小头疼程度。
若零崎无论如何也不会从Vi开始看到Vj,则输出jujue(拒绝
输入样例
3 2
-1 0 1
1 -1 2
2 3 -1
1 3
2 2
输出样例
1
jujue
Hint
有向图的算法你们还记得多少?
环路拒绝!
解题思路:
这题就是考察Floyd算法的应用。不同的是:这题把没有通路的两个点之间的距离设置为-1,而不是Floyd算法中的INF。所以我们只要在输入的时候,把原来为-1的连接权值设置为INF就可以使用原来的算法了。
解释一下Floyd算法中,为什么使用中间点更新最短路径和中间点的插入顺序没有关系^V^(之前一直没有想明白 -w- ):因为对于最短路径来说,最短路径上的子路径一定也是最短路径。它上面经过任意三点A,B,C之间的距离一定会短于AC之间的直接距离(要不然这就是一个新的路径了呀~)所以每次更新,只要插入点X在最短路径上,X就一定会被插入!!! 也就是说:最短路径上的点一定会被加入最终的路径选择之中!lol
解题代码:
#include D.Nova君有N种方式让jhljx待不下去
题目描述
Nova君是一个游戏maniac,非常喜欢把游戏按照购买日期排好队,放在一起,以供观瞻,如下图所示。

每个游戏都有自己独一无二的位置,Nova君绝对不允许有任何错位。可众所周知,jhljx 是个爱作死的人,有一天,他打乱了Nova君的游戏放置,并笑嘻嘻的说:“你有N个游戏,我就有F(N)种方式让所有的游戏都不在正确的位置 上。”hhh,请问,Nova君有多少种方式让 jhljx 待不下去?
输入
多组测试数据,每组数据一行,为一个正整数N(1<=N<=20),表示Nova君游戏的个数
输出
对于每组数据,输出一行,表示所有游戏都不在正确位置的排列的种数
输入样例
1
2
输出样例
0
1
b
解题思路:
这道题就是考察错排问题。
算法如下:
先引入记号A[n],表示当n个元素放在n个位置,元素编号与位置编号各不对应的方法数。
第一步,把第n个元素放在一个位置,比如位置k,一共有n-1种方法;
第二步,放编号为k的元素,这时有两种情况:
⑴把它放到位置n,那么,对于剩下的n-1个元素,由于第k个元素放到了位置n,剩下n-2个元素就有A[n-2]种方法;
⑵第k个元素不把它放到位置n,这时,对于这n-1个元素,有A[n-1]种方法(原因:现在剩下的位置有:1,2,…,k-1,k+1,…,n;剩下的元素有:1,2,…,k-1,k,k+1,…,n-1,我们把元素k定义为新的元素n,这样一来,就出现了一个由n-1个元素组成的新的错排问题,即A[n-1]种情况)。
综上得到:A[n] = (n-1)*(A[n-2] + A[n-1])。
特殊地,A[1] = 0, A[2] = 1。
由上式,很容易能想到使用DP方法求解(毕竟只有20组数据),只是注意要用long long保存数据。
解题代码:
#include E. “伪”积分
题目描述
高数虐了Nova君两个学期,也让Nova君幸福了一个学期。
我们都知道,微积分在几何上的一个重要的应用就是计算曲边面积。
现在我们的任务是计算满足 { 0<=x<=1,0<=y<=1,y<=(sinx)/x } 这部分的面积(标记为S) 然而由于年代久远,Nova君似乎忘记了如何用正规的数学方法解答,但他还记得一个古老的方法,那就是抛针法,我们可以让大量的小点随机分布在整个正方形 内,最后统计在S内的点的个数即可进行下一步计算~众所周知,点数越多,答案越精确,每次投点的个数记为N(N<=100000000)(hhh, 有点多=。=)请用这种近似的方法输出 S 的面积。
输入
多组测试数据,每组输入一行,为一个正整数N,表示投点的个数
输出
每组数据输出一行,结果保留三位有效数字
输入样例
无
输出样例
无
解题思路:
其实就是使用随机数生成一系列随机点,最终利用如下公式求得点落在给定区域中的概率和面积:


/*吐槽一下:
1.有的同学吐槽不是4位数字。。是四位有效数字没错,因为个位数不是0。。。。
2.没有输入啊对不对,为什么题目描述要写有输入捏0.0。*/
解题代码:
#include F. 说好的ALS呢?
题目描述
每一个手办都是有灵魂的,下面这个高达手办,帅到爆炸有木有O-o。

然而要制作这样一件神器却要费不少功夫。假设现在某厂商引进了制作的整套流水车间,决定量产拯救世界。此车间有n条流水线,每条流水线线有m个装配站,编号都为1-m,每条工作线的第i个装配站都执行相同的功能。拼装一个手办要经过m个装配站才能加工完成,经过第i条工作线的第j个装配站要花费p[i][j]的时间,从第i个工作线移动到第j个工作线要花费t[i][j]的时间,请问制造一个高达最少时间是多少?
输入
多组测试数据
对于每一组测试数据,第一行两个整数输入 N,M(100>=N,M>0),分别代表N条工作线和每条线有M个装配站。
接下来N行每行M个数( N*M 的矩阵,第i行第j个数代表描述中的p[i][j] ),0<权值<=100。
接下来N行每行N个数( N*N的矩阵,第i行第j个数代表描述中的t[i][j] ),0<权值<=100。
输出
对于每组数据,输出一行,a+b的值
输入样例
3 3
10 1 10
8 5 10
10 10 2
0 5 2
1 0 5
1 1 0
输出样例
14
Hint
可用图论的知识做,加油~
解题思路:
用Floyd算法。
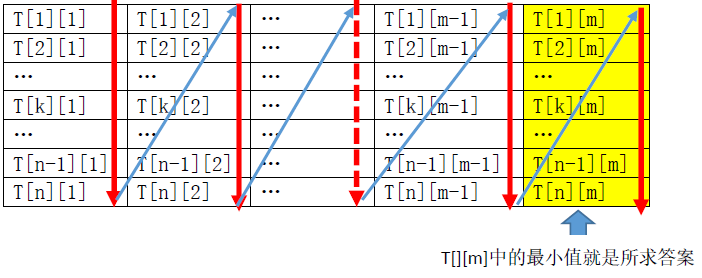
开一个T[n+1][m+1]的数组(从1开始,避免逻辑位置和物理位置的转换过程),T[i][j]表示从第i条线开始,到达第j个站所用的最短距离。然后使用DP思想对T[][]从T[][1]开始,逐渐更新到T[][m],最终求出数组T[][m]中的最小值,就是所求的最短时间。
状态转移方程如下:
T[i][j] = min(T[i][j], T[i-1][k]+t[k][j]+p[i][j])(k = 1,2,…,n)
直观感受一下更新顺序:
解题代码:
#include G.挑战神奇宝贝联盟
题目描述
这一天终于到了,Nova君终于集齐了所有道馆徽章,带着他的n只Pockmon准备挑战神奇宝贝联盟。谁知半路杀出火箭队的新成员jhljx,放 出了他的招牌英雄臭臭泥,让Nova君的n只神兽级Pockmon全部陷入中毒状态。Nova君自然没有理会jhljx同学,径直去了优购服务中心,想要 给Pockmon解毒。然而毕竟只是优购分中心,只有一台机器可以使用,而且每次只能给一只Pockmon解毒。假设n只Pockmon身上分别有 a1,a2,a3,,,an点毒素,每只Pockmon每秒钟可以自行解毒,消解1点毒素,而机器每秒钟可以消解k点毒素,由于在机器内时对 Pockmon体质有影响,不再自行消解毒素(也就是说,机器内的每秒消解k点,不在机器内的,每秒消解1点)。求问,Nova君最快得等待多少时间才能 让Pockmon们全部恢复?
PS:为了简化问题,最小时间单位以一秒为准,不可再分割时间进行操作
输入
多组测试数据
每组数据输入三行,第一行为一个正整数n (1<=n<=100000),代表Pockmon个数
第二行为n个正整数ai (1<=ai<=10^9),分别代表毒素点数
第三行为一个正整数k (1<=k<=10^9)
输出
对于每组数据,输出一行,表示让所有Pockmon恢复健康的最短时间
输入样例
3
2 3 9
5
3
2 3 6
5
输出样例
3
2
解题方法:
多谢福神给我提供了本题的思路指导 ^_^
为了方便处理,这题得做一下等价变换:题目中说:“机器内的每秒消解k点,不在机器内的,每秒消解1点”,这种处理方式等价于:“不在机器内的,每秒消解1点,机器内的,每秒多消解k-1点”。差别就在于,这样的话,所有的Pockmon每秒都会消除1点毒量,而进入机器的只是在这个基础之上额外增加了k-1点消除量,其实是简化了操作(额,不理解的话接着往下看就可以了)
这是一种基于假设和二分的方法:我们把中毒量记录在数组toxic_doses[]里面。同时我们记录最大的中毒量big和最小的中毒量small。(核心)假设最短用时为mid = (big+small)/2。那么:
(1) 对于toxic_doses[i]<=mid的宠物,我们不需要对其进行机器解毒操作,因为它们自身就可以在这段时间内完成解毒;
(2) 对于toxic_doses[i]>mid的宠物,我们需要对其进行机器解毒操作。
为了节省时间,我们把一个toxic_doses[i]>mid的宠物的中毒量分成两部分进行解毒操作:
a) 由于我们的等价转化,在mid时间内,宠物自身可以解除mid点毒量;
b) 剩下toxic_doses[i]-mid点毒量,要想不使总时间超过mid,这部分必须用机器解毒;又因为“最小时间单位以一秒为准,不可再分割时间进行操作”,所以这部分所用的时间为ceil((toxic_doses[i]-mid)/(k-1))
由以上分析,机器运行时间等于所有Pockmon占用机器的时间的总和totolTimeInMachine(即(2)b)中的时间总和)。
(1) totolTimeInMachine不超过mid,那么就说明:在mid时间内可以完成解毒操作。但是这时得到的mid值只是一个能完成解毒操作的时间,并不一定是最短时间,这时候就需要进一步查找可能的最小值,我们使用二分操作,即设置时间上下限[small,big]=[small,mid-1]并对这种时间设置重复上述操作;
(2) 如果totolTimeInMachine超过mid,则说明mid过短,我们得对mid进行放大操作,即设置时间上下限[small,big]=[mid+1,big],然后继续上述操作。
这就是大致的算法分析啦。没懂的话,配合着代码看,应该就不难理解了。
解题代码:
#include ![A[n]是一个升序排列好的数组](http://img.e-com-net.com/image/info8/65824cd0224c4ccb838280b38d9cd126.png)

