基于Python的PLA线性分类器的实现
线型分类器(PLA),可以看做是一个最简单的单层前馈神经网络。PLA的目的可以简要概括为:通过训练,将一系列二维平面上的点分开。
1、数据集
这里采用带标签【0,1】的二维数据集:
dataset = np.array([ # 此处用x,y形式的array来存储数据
((- 0.4, 0.3), 0),
((- 0.3, - 0.1), 0),
((- 0.2, 0.4), 0),
((- 0.1, 0.1), 0),
((0.6, - 0.5), 0), # 非线性分割点,后面可根据情况删掉
((0.8, 0.7), 1),
((0.9, - 0.5), 1),
((0.7, - 0.9), 1),
((0.8, 0.2), 1),
((0.4, - 0.6), 1)])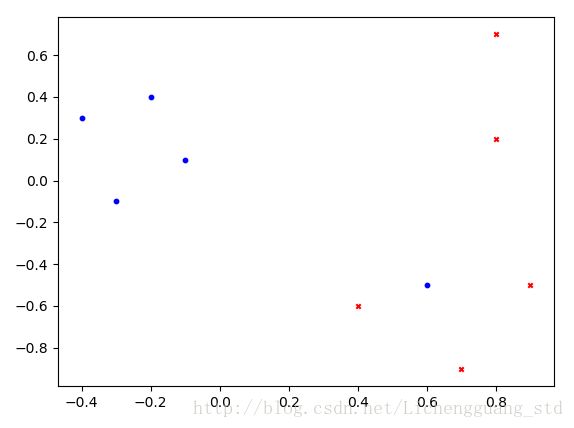
2、误差函数
定义误差函数的目的在于确定当前的权重向量是否需要修正。这里,本算法的误差确定较为粗略,仅根据权重向量与数据集向量的点积值正负来确定。
3、完整代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
dataset = np.array([ # 此处用x,y形式的array来存储数据
((- 0.4, 0.3), 0),
((- 0.3, - 0.1), 0),
((- 0.2, 0.4), 0),
((- 0.1, 0.1), 0),
((0.6, - 0.5), 0), # 非线性分割点
((0.8, 0.7), 1),
((0.9, - 0.5), 1),
((0.7, - 0.9), 1),
((0.8, 0.2), 1),
((0.4, - 0.6), 1)])
# 点积、误差、权重校正
w = np.array([0.001, 0.001])def sign(x, w): # 该函数的主要目的是判断点积值的正负
sign = w.T.dot(x)
return sign
def PLA(dataset, w):
i = 0
for x, y in dataset[:4]: # 按照x,y的形式来取出数据,for里面的这个循环只能循环5次,把前五个标签为0的数据训练完
x = np.array(x) # 将x向量化,此处的x为list而非向量
while sign(x, w) < 0:
w = w + 0.001 * x # 利用向量加法,不断修正w,使其偏向x
sign(x, w)
i += 1
print("i=", i, "w=", w, "error=", sign(x, w), "x=", x)
w0 = w
w = np.array([0.001, 0.001])
for x, y in dataset[5:9]: # 按照x,y的形式来取出数据,for里面的这个循环只能循环5次,把前五个标签为0的数据训练完
x = np.array(x) # 将x向量化,此处的x为list而非向量
while sign(x, w) > 0:
w = w - 0.001 * x # 利用向量加法,不断修正w,使其偏向x
sign(x, w)
i += 1
print("i=", i, "w=", w, "error=", sign(x, w), "x=", x)
w1 = w
return w0 + w1
w = PLA(dataset, w)
print("Final weight=", w)
ps = [v[0] for v in dataset]
fig = plt.figure()
ax1 = fig.add_subplot(111)
# 取出第二列的数据 画出散点图
ax1.scatter([v[0] for v in ps[: 5]], [v[1] for v in ps[: 5]], s=10, c='b', marker="o", label='O')
ax1.scatter([v[0] for v in ps[5:]], [v[1] for v in ps[5:]], s=10, c='r', marker="x", label='X')
# 画出当前权重向量
xw = [0, 100 * w[0]]
yw = [0, 100 * w[1]]
# plt.plot(xw, yw)
x = np.linspace(- 2, 2)
plt.show()