拒绝推断
拒绝推断
转载自微信号bigdatafengkong
转载连接:https://mp.weixin.qq.com/s/RnQXPUBJe8-NUvtPDho0vw
在做申请评分卡时,所使用的数据是审批接受的已知好坏状态的样本数据,然后用此评分对新的申请进行评估,这里会存在所谓"样本偏差"的问题,因为接受样本只是申请样本的一部分,此评分没有考虑拒绝样本的信息,在对总体申请进行评估时会有偏差。如果能够想办法将拒绝样本和接受样本放在一起建模,就是所说的“拒绝推断”。
先想想什么情况下不需要做拒绝推断?如果之前的审批策略不是很有效,相当于随机选择接受的客户,那么接受样本和拒绝样本的分布应该是一样的,这种情况就没必要做拒绝推断了。
相反,如果之前的审批策略越有效,接受样本和拒绝样本差别就越大,那么越有必要做拒绝推断。另外做拒绝推断也是为了更多更准确地找出好客户,降低成本,提高收益。
拒绝推断常用方法有三种,实验法、直接赋值法和模型扩展法。
(一)实验法
实验法就是在生产环境中做实验,积累全量数据。如在某一段时间内,接受所有申请,等该批申请客户有了风险表现后,直接在该样本上建模,所使用的数据和未来要预测的数据在分布上偏差较小。实验法其实是花钱买数据,需要承受较大的坏账损失,一般机构接受不了,更别说银行等受严监管的金融机构了。前两年现金贷火爆的时候,由于收益高,很多做现金贷的公司,除了验证身份、过一下黑名单等简单措施,所采取的风控手段很少,通过率极高,这样的环境相当于提供了一个天然的数据收集实验场。
(二)直接赋值法
直接赋值法是指通过外部数据或人工的方法,为拒绝样本打上好坏标签。比如通过查看外部数据发现此人在其他机构发生过很严重的违约行为,那么这种拒绝样本可以直接标记为坏,该方法需要花费一定的数据成本,并且有些外部数据较难获取。还可以让审批人员对拒绝客户进行复核,标记出认为违约可能性高的样本,不过此种方法也不经济,需要花费很多的人力,且加入了主观的人为因素,容易造成偏差。
(三)模型扩展法
最为常用的技术是模型扩展法,先用接受样本建模,然后预测拒绝样本的好坏,最后将拒绝样本和接受样本放在一起建模。模型扩展法有以下几种。
1、简单扩展法
可以拆解为几个步骤:
(1)在接受并已知好坏的样本上建模。
(2)用此模型为拒绝样本打分P(bad概率),设置一个阈值P0,大于P0标记为坏,小于P0标记为好。选择的阈值要确保拒绝样本的坏账率比接受样本的坏账率高,一般设置拒绝样本坏账率是接受样本坏账率的2-5倍,当然要结合客群特征、通过率等因素综合考虑。该方法的一个缺点是,拒绝样本的分类有一定的随机性。
(3)将打好标签的拒绝样本和接受样本放在一起,重新建模。
(4)重复(2)和(3)直至模型参数收敛,一般迭代两三次就能得到收敛模型。
2、拆分扩展法
拆分扩展法并不是将拒绝样本直接标记为好或坏,而是根据打分概率将一个拒绝样本拆分成一个好样本和一个坏样本,打分概率为权重。具体可以按以下步骤进行:
(1)在接受并已知好坏的样本上建模。
(2)用此模型为第i个拒绝样本打分Pi(bad概率),然后将该拒绝样本拆分成一个坏样本和一个好样本,坏样本的权重为Pi,好样本的权重为1-Pi,而每个接受样本的权重均设置为1,这时可以根据权重计算坏账率。还可以调整拆分后的拒绝样本的权重,使拒绝样本的坏账率是接受样本坏账率的F倍,比如坏样本的权重调整为Pi*C/(Pi*C+1-Pi),好样本的权重调整为(1-Pi)/(Pi*C+1-Pi)。
(3)将(2)拆分后的拒绝样本和接受样本放在一起建模。
(4)重复(2)和(3)直至模型参数收敛。
3、分段扩展法
上述所说的简单扩展,将拒绝样本按照某个阈值采用一刀切的方式分成好样本和坏样本,这样的切分使拒绝样本的违约分布和接受样本差别极大,而分段扩展正好修正这一缺点。步骤如下:
(1)在接受并已知好坏的样本上建模。
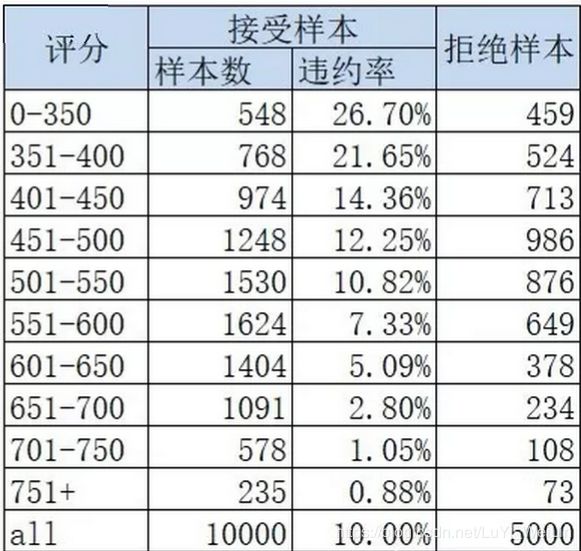
(2)然后为接受样本和拒绝样本打分score,下图为每个评分区间内接受样本的违约分布和拒绝样本的数量:
接下来,按照各分数段对拒绝样本打标签。一般拒绝样本的违约率高于接受样本,这里假设拒绝样本的违约率是同分数段接受样本的2倍。以0-350分数段为例,接受样本的违约率为26.7%,设置拒绝样本的违约率为53.4%,然后根据这个违约率,随机的将该分数段内的样本设置成好和坏,或者根据分数高低,高分数设置为好,低分数设置为坏,就像简单扩展法中的做法。下图为打好标签的拒绝样本的违约分布:
(3)将(2)中打好标签的拒绝样本和接受样本放在一起建模。
(4)重复(2)和(3)直至模型参数收敛。
4、其他方法
除了上述几种方法,还有一些其他方法,比如可以通过近邻(Nearest Neighbor)算法预测拒绝样本的好坏,然后用拒绝样本和接受样本建立模型。
其实,拒绝推断一直存在争议,有人认为没必要做,有人认为有必要做。但在条件允许的情况下,比如若有充足的数据和时间,尝试做一下,两者做出来的结果做个对比,总不是坏事。