2.sklearn—评价指标大全（平均误差、均方误差、混淆矩阵、准确率、查全率、查准率、召回率、特异度，F1-score、G-mean、KS值、ROC曲线、AUC值、损失函数、结构风险最小）

1. 回归问题中的各种误差

1.1 绝对误差和相对误差

• 绝对误差：
  $$E=Y-\hat{Y}$$
• 相对误差：
  $$e=\frac{Y-\hat{Y}}{Y}$$

1.2 平均绝对误差

英文：MeanAbsoluteError,MAE

$$MAE=\frac{1}{n}\sum _{i=1}^n|Y_i-{\hat{Y}}_i|$$

1.3 均方误差！！！zei重要！！！！

英文：Mean Square Error,MSE
$$mse=\frac{1}{n}\sum _{i=1}^n(Y_i-{\hat{Y}}_i{)}^2$$

1.4 均方根误差

英文：Root Mean Square Error,RMSE
$$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n(Y_i-{\hat{Y}}_i{)}^2}$$

1.5 平均绝对百分误差

英文：Mean Absolute Percentage Error,MAPE
$$MAPE=\frac{1}{n}\sum _{i=1}^n|\frac{Y_i-\widehat{Y_i}}{Y_i}|$$

一般认为MAPE < 10的情况下，预测精度高。

2. 分类问题判误指标（机器学习）

2.1 二分类的混淆矩阵

.	（真实）肯定	（真实）否定
（预测）肯定	TP	FP
（预测）否定	FN	TN

TP:True Posirive:正确的肯定的分类数
TN:True Negatives:正确的否定的分类数
FP:False Positive:错误的肯定的分类数
FN:False Negatives:错误的否定

2.2 二级指标

2.2.1 准确率（Accuracy）

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$$

2.2.2 精确率（Precision）——查准率

$$Precision=\frac{TP}{TP+FP}$$

2.2.3 查全率、召回率、反馈率（Recall）,也称灵敏度（Sensitivity）-TPR

$$Recall=\frac{TP}{TP+FN}$$

2.2.4 特异度（Specificity）-TNR

$$Specificity=\frac{TN}{TN+FP}$$

2.2.5 FPR（假警报率）

$$FPR=\frac{FP}{FP+TN}$$

2.3 三级指标

2.3.1 F1_score

(1). 狭义F1
$$F_1=\frac{2\ast Precision\ast Recall}{Precision+Recall}$$

(2). 范式
$$F_{\beta }=\frac{(1+{\beta }^2)\ast Precision\ast Recall}{{\beta }^2\ast Precision+Recall}$$

$${\beta }^2=\frac{Recal{l}_{weight}}{Precisio{n}_{weight}}$$

$$Recal{l}_{weight}+Precisio{n}_{weight}=1$$

这个公式具体的推导，推荐这篇博客https://blog.csdn.net/shy19890510/article/details/79501582

• 解释：
• 在实际的情况中可能对于查全率和查准率的要求不同、比如对于推荐系统而言，查准率比较重要；而对于逃犯系统，查全率重要。

2.3.2 G-mean

$$G-mean=\sqrt{Recall\ast Specificity}$$

在数据不平衡的时候，这个指标很有参考价值。

2.3.3 KS值

$$KS=max(TPR-FPR)$$

2.4 ROC曲线、Auc值、KS曲线、Lift

这边推荐三篇博客：
第一篇传送门https://blog.csdn.net/shy19890510/article/details/79501582
第二篇传送门https://blog.csdn.net/lz_peter/article/details/78054914
第三篇传送门https://blog.csdn.net/lz_peter/article/details/79296431

2.4.1 ROC曲线、Auc值

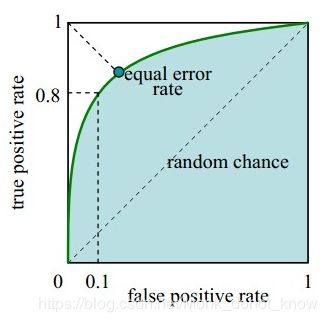
绿色的线就是ROC曲线，注意观察横纵坐标，分别为FPR、TPR。
曲线下方的绿色阴影面积就是AUC值。

2.4.2 KS

KS(Kolmogorov-Smirnov)值越大，表示模型能够将正、负客户区分开的程度越大。
这个跟模型设置的判断的阈值有很大关系。

3. 损失函数和风险函数

这部分内容总结自：李航,统计学习方法[M],北京:清华大学出版社,2012.
这本书特别基础！墙裂推荐！！！入门必备！

3.1 损失函数(loss function)

3.1.1 0-1损失函数

$$L(Y,f(X))=\{\begin{array}{ll}1& \text{Y!=f(X)}\\ 0& \text{Y=f(X)}\end{array}$$

3.1.2 平方损失函数

$$L(Y,f(X))=(Y-f(X){)}^2$$

3.1.3 绝对损失函数

$$L(Y,f(X))=|Y-f(X)|$$

3.1.4 对数损失函数

$$L(Y,P(Y|X))=-logP(Y|X)$$

3.2 风险函数（期望损失）、经验风险

损失函数越小，模型就越好。假设(X,Y)遵循联合分布P(X,Y),所以损失函数的期望就是：

3.2.1 期望损失

损失函数基于联合分布P(X,Y)的期望损失，也称为风险函数：
$$R_{exp}(f)=E_P[L(Y,f(X))]={\int }_{x\ast y}L(y,f(x))P(x,y)dxdy$$
但是P(X,Y)一般是未知的，不可以直接计算期望。

3.2.2 经验风险（empirical risk）

训练集样本 的平均损失
$$R_{exp}(f)=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))$$
根据大数定理，当N足够大的时候，经验风险趋于期望风险，所以用经验风险去估计期望风险。由于实际训练的时候，样本量数目有限，因此需要对经验风险有一定的矫正，就有了结构风险的概念，在下一节（4）说明。

3.2.3 关于统计建模和机器学习的分水岭

这是我个人理解，欢迎指正。
由此就出现一个分界线：对于传统的统计模型，我们是基于数据模拟的分布，选择合适的模型建模，因此，统计建模之后，由于数据是在严格的分布情况下建模，比如线性模型、零膨胀负二项模型、逻辑回归等（优势比的概念去解释），模型的可解释性很强。这里根本上的依据是中心极限定理、大数定理；
而实际上对于很多事实的情况就是，对于联合分布P(X,Y)是未知的，因此会采用各种机器学习的方法去尽可能拟合数据、预测未来走势。这时候就弱化了对于数据分布上的要求。那为什么基于历史数据可以预测新数据呢？这里主要依据的是霍夫丁不等式。

3.3监督学习的一个悖论（病态问题）

一方面根据期望风险最小学习模型要用到联合分布，一方面联合分布又未知，所以监督学习就成为了一个病态问题。

4. 经验风险最小化与结构风险最小化

这基本上就是统计建模和机器学习建模的所有模型的最最最基础最最最核心的知识！！！
它本质上还是架在损失函数上面去讨论问题。

4.1 经验风险最小化(empirical risk minimization,ERM)

$$\underset{f\in F}{\min }\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))$$
F为假设空间

很常见的极大似然估计就是一个广泛的应用！当模型是条件概率 分布时，损失函数是对数损失函数的时候，经验风险最小化等价于极大似然估计。

4.2 结构风险最小化（structural risk minimization,SRM）

$$R_{srm}(f)=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$$
其中：J(f)是模型的复杂度，也成为罚项、正则化项。
到此，监督学习问题变为了，寻求结构风险最小话的优化求解。
$$\underset{f\in F}{\min }{R}_{srm}(f)=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$$