机器学习之K-means算法（Python描述）基础

Python 2.7
IDE Pycharm 5.0.3
numpy 1.11.0
matplotlib 1.5.1

可以扩展阅读：
1.(大)数据处理：从txt到数据可视化
2.机器学习之K-近邻算法（Python描述）基础
3.机器学习之K-近邻算法（Python描述）实战百维万组数据

数据及参考代码
github地址，下载压缩包，ch10

---

前言

从程序上读懂每一行，才是了解算法的开始。

---

什么是K-means?

一句话：一堆数据我也不知道是啥玩意的(无标签)的扔给你，你给我分一下，哪一堆属于一类。这就是聚类！

---

Knn VS K-means

knn表现的是有监督情况下，也就是我都知道标签了，载扔进去一个没有带标签的，根据特性(特征)，你给我判断出来，这个属于哪一类，就像分类匹配一样。

K-means表现的是无监督情况下，我不知道标签，我只有数据集，那么从那么大一堆数据集中，我需要找出“规律”，也就是数据挖掘的一部分了，哪一些数据属于同一个类(虽然我并不知道这个类叫什么，whatever)，

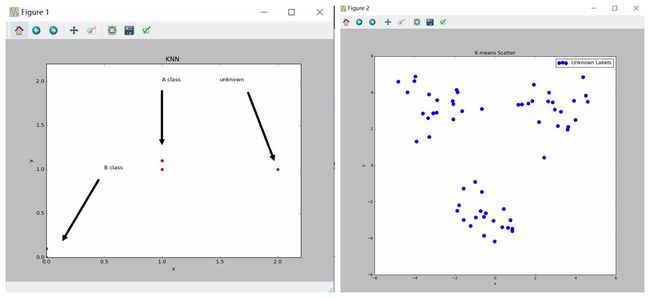
来张图可能清楚点。左边的是knn，主要用于未知点的分类，右图是k-means，主要用于聚类(当然也可以用来对未知点的聚类判断)

还是不理解分类和聚类请看我在知乎上的回答@徐凯–聚类与分类有什么区别？

---

数据形式

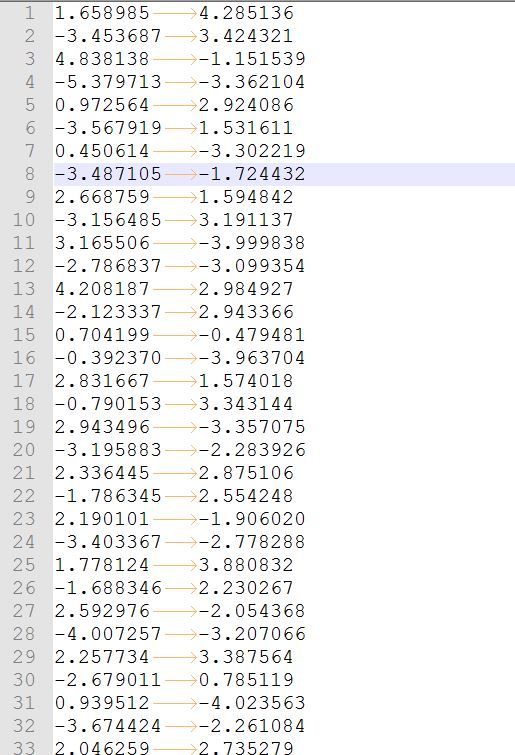
ok，还是老样子的txt格式，数据的清洗和读取必不可少，至于怎么将txt写入矩阵，请参考（大）数据处理：从txt到数据可视化或者以下代码注释

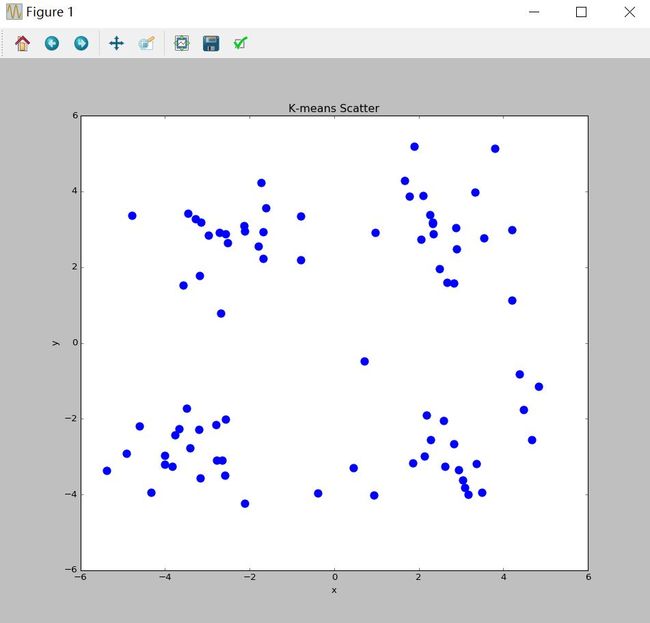
展示以下大概是这样的，虽然，我们一看就能知道，簇中心也就是聚类中心大概的位置，但是机器并不知道，怎么计算出聚类中心，这就是k-means干的活了！

---

K-Means算法流程

具体的K-Means原理不再累述，很详细的请见
深入浅出K-Means算法

我这里用自己的话概括下

1. 随机选k个点作为初代的聚类中心点
2. 计算其余各点到这些聚类中心点的‘距离’，并选择距离自己最近的聚类点作为自己的类，给自己打上标签
3. 属于同一簇的一群点进行取质心运算，计算新的簇中心
4. 重复2~3，直到簇中心不再改变

---

代码–K-means基础

# -*- coding: utf-8 -*-
import math
from numpy import *
#C:\\Users\\MrLevo\\Desktop\\machine_learning_in_action\\Ch10\\testSet.txt

#载入数据，清洗数据保存为矩阵形式
def loadDataSet(filename):
    fr = open(filename)
    lines = fr.readlines()
    dataMat = []
    for line in lines:
        result = line.strip().split('\t')
        fltline = map(float,result)
        dataMat.append(fltline)
    return dataMat


#向量计算距离
def distEclud(vecA,vecB):
    return sqrt(sum(power(vecA-vecB,2)))


# 给定数据集构建一个包含k个随机质心的集合，
def randCent(dataSet,k):
    n = shape(dataSet)[1] # 计算列数

    centroids = mat(zeros((k,n)))
    for j in range(n):
        minJ = min(dataSet[:,j]) #取每列最小值
        rangeJ = float(max(dataSet[:,j])-minJ)
        centroids[:,j] = minJ + rangeJ*random.rand(k,1) # random.rand(k,1)构建k行一列，每行代表二维的质心坐标
        #random.rand(2,1)#产生两行一列0~1随机数
    return centroids

#minJ + rangeJ*random.rand(k,1)自动扩充阵进行匹配，实现不同维数矩阵相加,列需相同


#一切都是对象
def kMeans(dataSet,k,distMeas = distEclud,creatCent = randCent):
    m = shape(dataSet)[0] # 行数
    clusterAssment = mat(zeros((m,2))) # 建立簇分配结果矩阵，第一列存索引，第二列存误差
    centroids = creatCent(dataSet,k) #聚类点
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            minDist = inf # 无穷大
            minIndex = -1 #初始化
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:]) # 计算各点与新的聚类中心的距离
                if distJI < minDist: # 存储最小值，存储最小值所在位置
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i,0] != minIndex:
                clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2
        print centroids
        for cent in range(k):

            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A== cent)[0]]
            # nonzeros(a==k)返回数组a中值不为k的元素的下标
            #print type(ptsInClust)
            '''
            #上式理解不了可见下面的，效果一样
            #方法二把同一类点抓出来

            ptsInClust=[]
            for j in range(m):
                if clusterAssment[j,0]==cent:
                    ptsInClust.append(dataSet[j].tolist()[0])
            ptsInClust = mat(ptsInClust)
            #tolist  http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.tolist.html
            '''

            centroids[cent,:] = mean(ptsInClust,axis=0) # 沿矩阵列方向进行均值计算,重新计算质心
    return centroids,clusterAssment


dataMat =mat(loadDataSet('C:\\Users\\MrLevo\\Desktop\\machine_learning_in_action\\Ch10\\testSet.txt'))
myCentroids,clustAssing = kMeans(dataMat,4)

IDE上输出

[[ 0.44698578  3.66996803]
 [ 4.4566098   1.69900322]
 [-1.54424114  3.58626959]
 [ 4.44813429  1.63720788]]

 ...

 [[-2.46154315  2.78737555]
 [ 2.6265299   3.10868015]
 [-3.53973889 -2.89384326]
 [ 2.65077367 -2.79019029]]
#四个聚类中心坐标如上，从图中可以看出，大概是这么个情况

---

设定不同k值，它会怎么聚类呢

以下是不同k的时候聚类情况

---

K-means出现的问题

收敛于局部最小，而不是全局最小，因为刚开始的聚类中心是随机给定的，所以搞不好就陷入局部最小了，而度量聚类效果的指标是误差平方和SSE，误差越大，簇的效果越不好，解决这个问题的方法之一就是二分K-means

---

什么是二分K-means

简单的说，就是将所有点先看成一个粗，然后簇一分为二，选择其中的一个簇继续划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。

实现过程

---

二分K-means代码

在原有代码基础上，添加biKmeans函数

# 构建二分k-均值聚类
def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2))) # 初始化，簇点都为0
    centroid0 = mean(dataSet, axis=0).tolist()[0] # 起始第一个聚类点，即所有点的质心

    centList =[centroid0] # 质心存在一个列表中

    for j in range(m):#calc initial Error
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
        # 计算各点与簇的距离，均方误差，大家都为簇0的群

    while (len(centList) < k):

        lowestSSE = inf
        for i in range(len(centList)):

            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i
            # 找出归为一类簇的点的集合，之后再进行二分，在其中的簇的群下再划分簇
            #第一次循环时，i=0，相当于，一整个数据集都是属于0簇，取了全部的dataSet数据

            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
            #开始正常的一次二分簇点
            #splitClustAss，类似于[0   2.3243]之类的，第一列是簇类，第二列是簇内点到簇点的误差

            sseSplit = sum(splitClustAss[:,1]) # 再分后的误差和
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1]) # 没分之前的误差
            print "sseSplit: ",sseSplit
            print "sseNotSplit: ",sseNotSplit
            #至于第一次运行为什么出现seeNoSplit=0的情况，因为nonzero(clusterAssment[:,0].A!=i)[0]不存在，第一次的时候都属于编号为0的簇

            if (sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
                # copy用法http://www.cnblogs.com/BeginMan/p/3197649.html

        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        #至于nonzero(bestClustAss[:,0].A == 1)[0]其中的==1这簇点，由kMeans产生

        print 'the bestCentToSplit is: ',bestCentToSplit
        print 'the len of bestClustAss is: ', len(bestClustAss)

        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids


        centList.append(bestNewCents[1,:].tolist()[0])

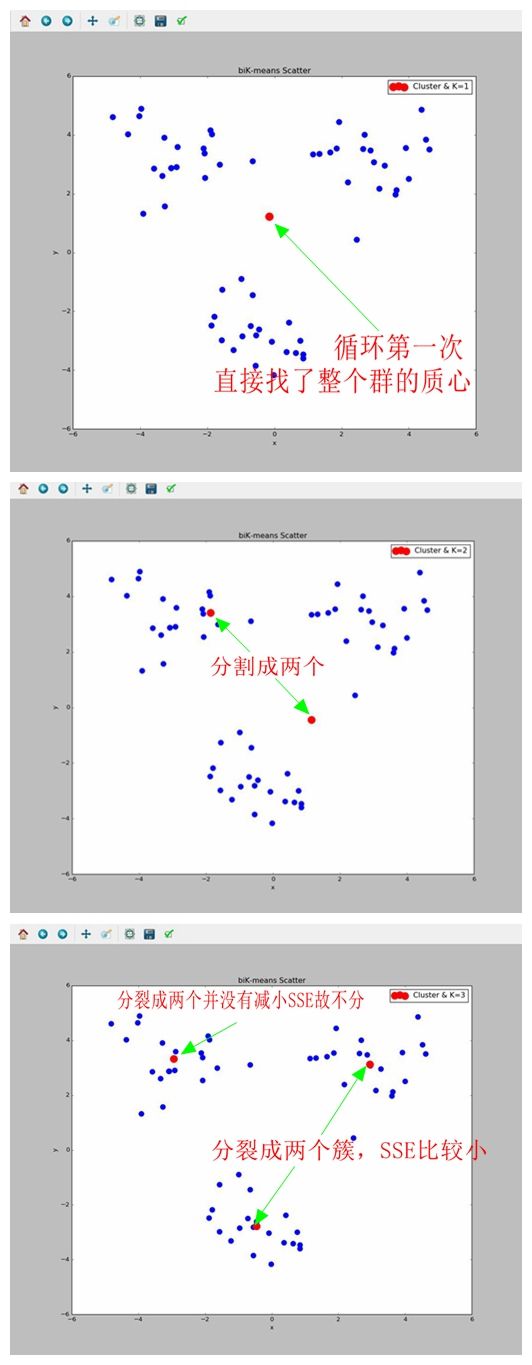
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE

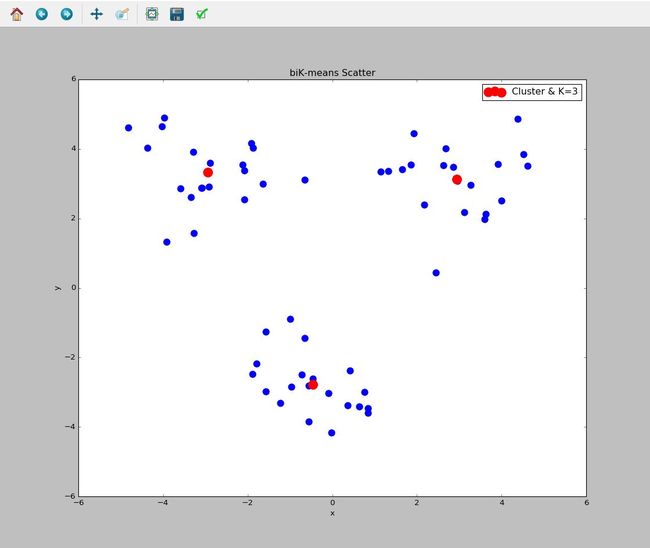
    return mat(centList), clusterAssment

效果下图可见，所以要讲的都写在注释上了，好好读代码，才是理解算法的唯一道路，光知道算法咋回事，自己重构不出，以后还是会忘的。

---

附录-matplotlib画图代码

# -*- coding: utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
import kMeans as km
#注意导入自己的Kmeans的py文件

data3 = mat(km.loadDataSet('C:\\Users\\MrLevo\\Desktop\\machine_learning_in_action\\Ch10\\testSet2.txt'))
centList,myNewAssments =km.biKmeans(data3,3)


###################创建图表2####################

plt.figure(2) #创建图表2

ax3 = plt.subplot() # 图表2中创建子图1
plt.title("biK-means Scatter")
plt.xlabel('x')
plt.ylabel('y')

ax3.scatter(data3[:,0],data3[:,1],color='b',marker='o',s=100)
ax3.scatter(centList[:,0],centList[:,1],color='r',marker='o',s=200,label='Cluster & K=3')


#显示label位置的函数

ax3.legend(loc='upper right')
plt.show()

---

核心语句解析

ptsInClust = dataSet[nonzero(clusterAssment[:,0].A== cent)[0]]

nonzeros(a)返回数组a中值不为零的元素的下标，它的返回值是一个长度为a.ndim(数组a的轴数)的元组，元组的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值。

举例如下

>>> b1 = np.array([True, False, True, False])
>>> np.nonzero(b1)
    (array([0, 2]),)

>>> b2 = np.array([[True, False, True], [True, False, False]])
>>> np.nonzero(b2)
    (array([0, 0, 1]), array([0, 2, 0]))

再来个例子补充下

>>> a = np.arange(3*4*5).reshape(3,4,5)
>>> a[b2]
array([[ 0,  1,  2,  3,  4],
       [10, 11, 12, 13, 14],
       [20, 21, 22, 23, 24]])
>>> a[np.nonzero(b2)]
array([[ 0,  1,  2,  3,  4],
       [10, 11, 12, 13, 14],
       [20, 21, 22, 23, 24]]))

也就是说，找到True的条件，返回索引，ok，这就够用来解释那句话的了，因为返回的是array形式的，所以需要再对应的取值，具体的可以看源代码的解释语句，我还另外的写了个实现一样功能的代码片段，注释起来了，实现的是同样的算法，希望理解结构的时候能帮到你

    ptsInClust=[]
    for j in range(m):
        if clusterAssment[j,0]==cent:
            ptsInClust.append(dataSet[j].tolist()[0])
    ptsInClust = mat(ptsInClust)
    #tolist用法  http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.tolist.html

---

致谢

利用python进行数据分析.Wes McKinney著
机器学习实战.Peter Harrington著
@stackoverflow–pyplot scatter plot marker size
@转–Python图表绘制：matplotlib绘图库入门
@BeginMan–深入Python(4):深拷贝和浅拷贝
@转–深入浅出K-Means算法
@MrLevo520–（大）数据处理：从txt到数据可视化
@MrLevo520–机器学习之K-近邻算法（Python描述）基础
@MrLevo520–机器学习之K-近邻算法（Python描述）实战百维万组数据