最大网络流之Ford-Fulkerson算法和ScalingFord-Fulkerson算法
1.最大网络流问题介绍
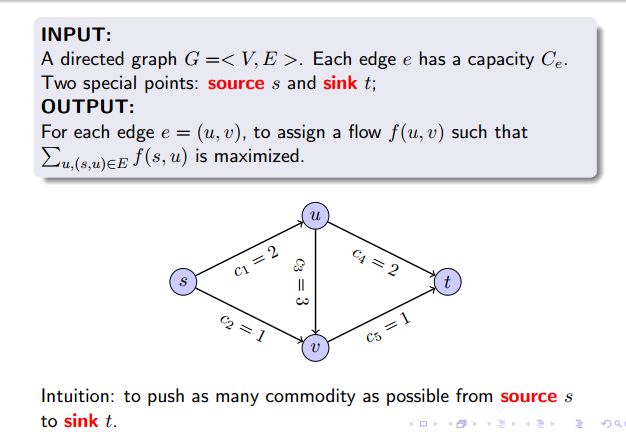
我们要解决的问题就是怎样分配,使得从 城市s 流出的货物到城市 s 的黄金最多,并且图中相邻城市之间实际运输的黄金数量不能超过他们的容量 c .
当然我们可以不加思索的用我们的超级武器$GLPK$来解决此问题,但这个问题比一般的线性规划问题更特殊,图的很多性质我们可以派上用场,关于图的知识可参见算法导论。下面我们介绍非常一个非常有套路的算法和它的改进版本。
2.Ford-Fulkerson算法
1956年,Lester Randolph Ford Jr. and Delbert Ray Fulkerson提出了Ford-Fulkerson算法。
Ford-Fulkerson算法原理如下:
Let p be a simple s − t path in residual graph Gf, called augmentation path. We define bottleneck(p, f) as the minimum capacity of edges in path p.
Ford-Fulkerson algorithm:
1: Initialize f(e) = 0 for all e.
2: while there is an s − t path in residual graph Gf do
3: arbitrarily choose an s − t path p in Gf;
4: f =augment(p, f);
5: end while
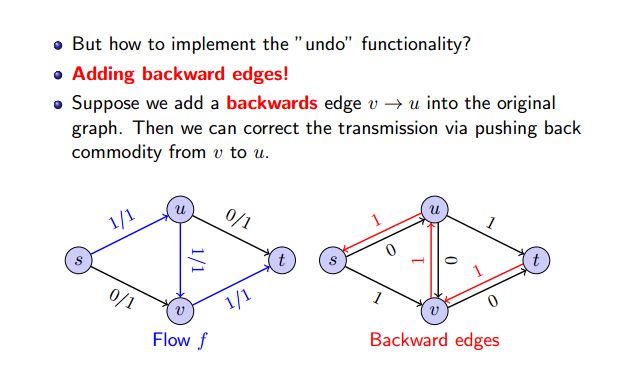
6: return f;该算法的最金典之处在于每当一条边上从起点节点向端点节点运输$f(u,v)$黄金时,则增加一条方向边$v->u$,其运输容量为$f(u,v)$.具体如下图所示
2.1Ford-Fulkerson算法具体应用
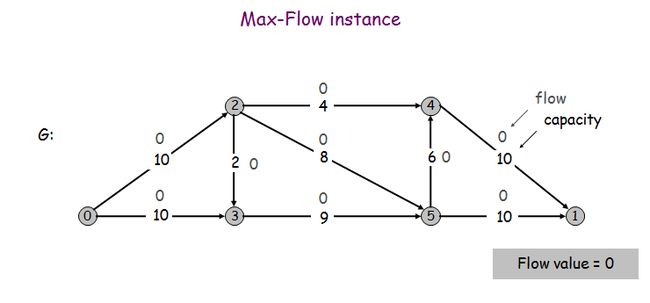
问题如下图,求从城市0到城市1的最大流
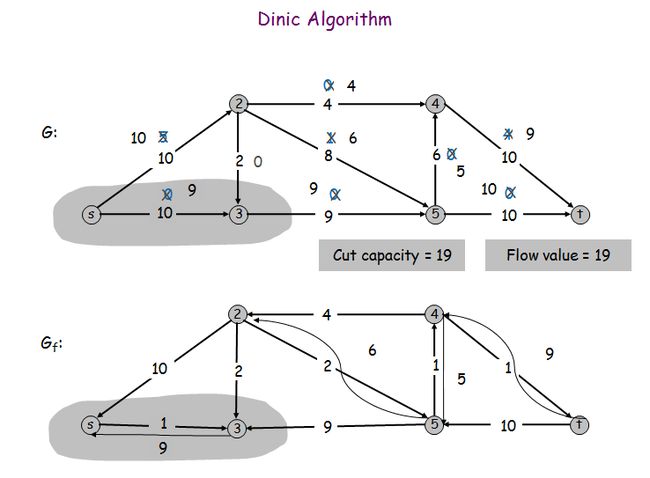
我们跑Ford-Fulkerson算法最后得到的流图如下:
具体程序如下:
/***********************************************************
Description:FordFulkerson算法求解网络最大流
Author:Robert.TY
Date:2016.11.30
************************************************************/
#includefor(int i=0;i<6;i++){
for(int j=0;j<6;j++){
graph[i][j]=tempgraph[i][j];
}
}
}
int FordFulkersonMaxFlow(int s, int t);//FordFulkerson算法求解最大流
bool PathSearch( int s, int t, int path[6]);//路径查询
int Augment(int path[6],int s,int t);// 增加流操作
void ShowResult(){
max_flow=FordFulkersonMaxFlow( 0, 1);
cout<<"max_flow="<int main(){
int V = 6;
int graph[6][6] = { { 0, 0, 10, 10, 0, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 2, 4, 8 },
{ 0, 0, 0, 0, 0, 9 },
{ 0, 10, 0, 0, 0, 0 },
{ 0, 10, 0, 0, 6, 0 } };
cout<<"输出原始网络流图的邻接矩阵:"<for(int i=0;i<6;i++){
for(int j=0;j<6;j++){
cout<5)<" ";
}
cout<cout<<"输出完毕:"<return 1;
}
int Max_Network_Flow::FordFulkersonMaxFlow(int s, int t){
int maxFlow = 0;
int path[6];
while(PathSearch( s, t, path)==1){//查询一条可行路径
maxFlow+=Augment(path,s,t);//再该路径进行增流操作
}
cout<<"最后网络流的邻接矩阵:"<for(int i=0;i<6;i++){
for(int j=0;j<6;j++){
cout<5)<" ";
}
cout<return maxFlow;
}
bool Max_Network_Flow::PathSearch( int s, int t, int path[6]) {
bool visited[6] ;
queue<int> queue1;
queue1.push(s);
visited[s] = true;
//标准的BFS算法
while(queue1.size() > 0){
int top = queue1.front();//返回队列头部的元素,
queue1.pop();//出队操作
for(int i=0; iif(!visited[i] && graph[top][i] > 0){//当节点i没有被访问,没有在队列当中且是top节点的邻居时
queue1.push(i);
visited[i] = true;
path[i] = top;
}
}
}
return visited[t] == true;
}
int Max_Network_Flow:: Augment(int path[6],int s,int t){
int min_flow =INT_MAX;
//找到当前路径中最小的流量 bottleneck
for(int v=t; v != s; v=path[v]){
int u = path[v];
min_flow=min_flow>graph[u][v]?graph[u][v]:min_flow;
}
//cout<<"min_flow="<
cout<//更新路径中的每条边反向边的权值增加min_flow,正向边的权值减少min_flow
for(int v=t; v != s; v=path[v]){
int u = path[v];
graph[u][v] -= min_flow;
graph[v][u] += min_flow;
}
return min_flow;
} 求解结果如下:
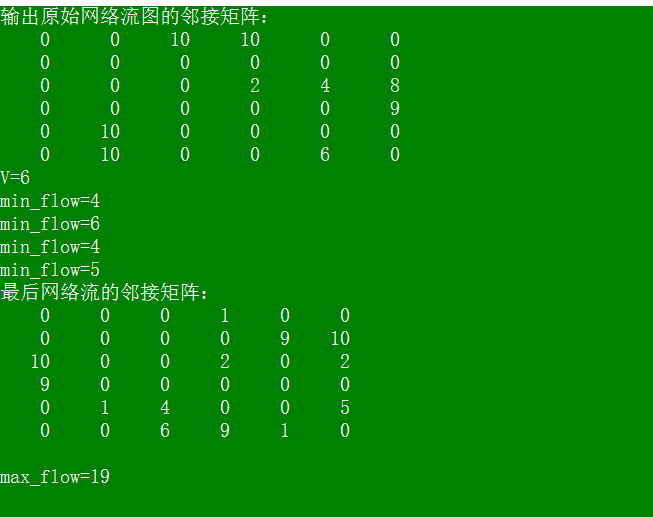
Ford-Fulkerson算法时间复杂度分析:

2.3Ford-Fulkerson算法总结
1:In the analysis of Ford-Fulkerson algorithm, the integer restriction of capacities is important: the bottleneck edge leads to an increase of at least 1.
2:The analysis doesn’t hold if the capacities can be irrational. In fact, the flow might be increased by a smaller and smaller number and the iteration will be endless.
3:Worse yet, this endless iteration might not converge to the
maximum flow.
3.ScalingFord-Fulkerson算法
针对Ford-Fulkerson算法, Uri Zwick提出改进,即ScalingFord-Fulkerson算法。
下面给出一个例子说明Ford-Fulkerson算法的缺点:
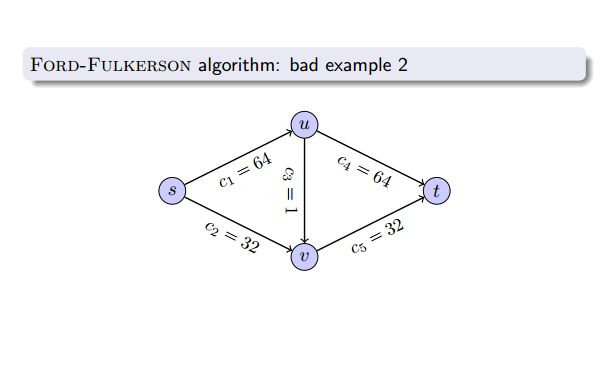
当我们跑Ford-Fulkerson算法时,很有可能是出现这样的糟糕情况,如下:
第一步:

第二步:
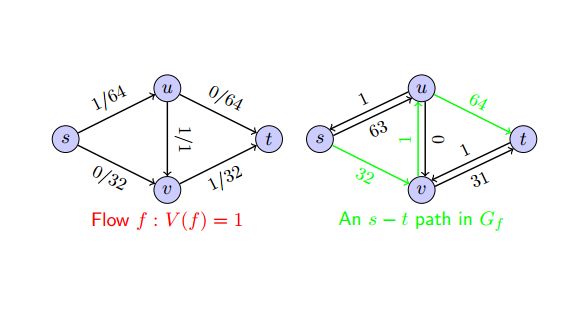
第三步:
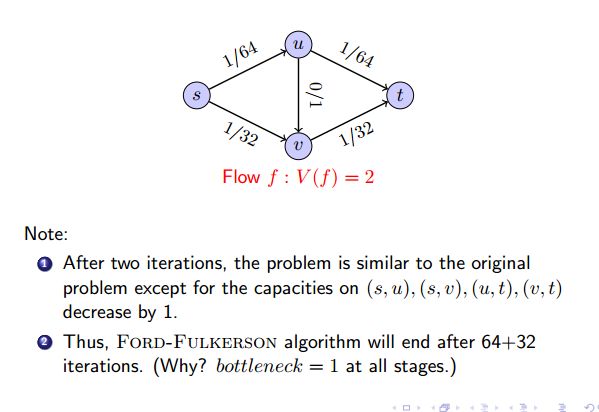
我们提出改进技术:

Scaling Ford-Fulkerson algorithm原理如下:
Scaling Ford-Fulkerson algorithm:
1: Initialize f(e) = 0 for all e.
2: Let ∆ = C;
3: while ∆ ≥ 1 do
4: while there is an s − t path in Gf(∆) do
5: choose an s − t path p;
6: f =augment(p, f);
7: end while
8: ∆ = ∆/2;
9: end while
10: return f;Intuition: flow is augmented in a large step size whenever possible; otherwise, the step size is reduced. Step size is controlled via removing the “small” edges out of residual graph.
Note: ∆ turns to be 1 finally; thus no edge in residual graph will be neglected.
3.1 Scaling Ford-Fulkerson algorithm具体应用
对于上面这个问题,我们用ScalingFord-Fulkerson算法求解:
具体程序如下:
/***********************************************************
Description:ScalingFordFulkerson算法求解网络最大流
Author:Robert.TY
Date:2016.11.30
************************************************************/
#includefor(int j=0;jint Scaling_FordFulkersonMaxFlow(int s, int t,int tempdelta);//FordFulkerson算法求解最大流
bool PathSearch(int s, int t, int path[Vnum],int delta);//路径查询
int Augment(int cur_flow,int path[Vnum],int s,int t);// 增加流操作
void ShowResult(int start,int end,int startdelta){
max_flow=Scaling_FordFulkersonMaxFlow(start, end,startdelta);
cout<"max_flow="<int main(){
/* int V = 6;
int graph[Vnum][Vnum] = { { 0, 0, 10, 10, 0, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 2, 4, 8 },
{ 0, 0, 0, 0, 0, 9 },
{ 0, 10, 0, 0, 0, 0 },
{ 0, 10, 0, 0, 6, 0 } }; */
int V = 4;
int graph[Vnum][Vnum] = { { 0, 64, 32, 0 },
{ 0, 0, 1, 64 },
{ 0, 0, 0, 32 },
{ 0, 0, 0, 0 }};
cout<<"输出原始网络流图的邻接矩阵:"<for(int i=0;ifor(int j=0;jcout<5)<" ";
}
cout<int startdelta=96;
int start=0;//出发节点
int end=3;//目的节点
Max_Network_Flow graph1(V,graph);
graph1.ShowResult(start,end,startdelta) ;
return 1;
}
int Max_Network_Flow::Scaling_FordFulkersonMaxFlow(int s, int t,int tempdelta){
int maxFlow = 0;
int path[Vnum];
int delta=tempdelta;
while(delta>=1){
cout<<"delta="<while(PathSearch( s, t, path,delta)==1){//查询可行路径
cout<<"当delta="<"时,找到路径"<//再该路径进行增流操作
}
delta=delta/2;
}
cout<<"最后网络流的邻接矩阵:"<for(int i=0;ifor(int j=0;jcout<5)<" ";
}
cout<return maxFlow;
}
bool Max_Network_Flow::PathSearch( int s, int t, int path[Vnum],int delta) {
bool visited[Vnum] ;
queue<int> queue1;
queue1.push(s);
visited[s] = true;
//标准的BFS算法
while(queue1.size() > 0){
int top = queue1.front();//返回队列头部的元素,
queue1.pop();//出队操作
for(int i=0; iif(!visited[i] && graph[top][i] >= delta){//当节点i没有被访问,没有在队列当中且是top节点的邻居时
queue1.push(i);
visited[i] = true;
path[i] = top;
}
}
}
return visited[t] == true;
}
int Max_Network_Flow:: Augment(int cur_flow,int path[Vnum],int s,int t){
int min_flow =INT_MAX;
//找到当前路径中最小的流量 bottleneck
for(int v=t; v != s; v=path[v]){
int u = path[v];
min_flow=min_flow>graph[u][v]?graph[u][v]:min_flow;
}
//cout<<"min_flow="<
//更新路径中的每条边反向边的权值增加min_flow,正向边的权值减少min_flow
for(int v=t; v != s; v=path[v]){
int u = path[v];
graph[u][v] -= min_flow;
graph[v][u] += min_flow;
}
cur_flow+=min_flow;
return cur_flow;
} 4.总结
Ford-Fulkerson算法和ScalingFord-Fulkerson算法的使用,其边的容量必须都是整数。读者可以尝试选用一条边为小数的情况跑一跑这两个算法,比如0.618.当然网络流算法还有很多其他的算法。
