LeetCode 刷题集(中等)

Leetcode3 无重复字符的最长子串

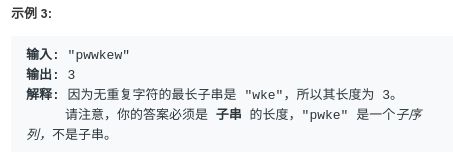
Golang 实现
实现思路：
首先需要一个map
记录每个出现的字母出现的位置 id_prev
当这个字母再次出现，新的位置为 id, 那么这个不重复字符串长度即为 id-id_prev
然后重新构造map

func lengthOfLongestSubstring(s string) int {
	longest := 0
	length := 0
	hash := make(map[rune]int, 0)
	for i, c := range s {
		if prev, ok := hash[c]; ok {
			length = i - prev
			hash = make(map[rune]int, 0)
			for j := i; j > prev; j-- {
				hash[rune(s[j])] = j
			}
		} else {
			length++
			hash[c] = i
		}

		if length > longest {
			longest = length
		}
	}
	return longest
}

队列的实现方式

Leetcode6 Z 字形变换

class Solution:
    def convert(self, s, numRows):
        if not numRows > 1:
            return s
        if numRows == 2:
            s1 = s[::2]
            s2 = s[1::2]
            s3 = s1 + s2

            return s3
        s_Initialize = [''] * numRows
        # print(s_row)
        i = 0
        n = len(s)
        while i < n:
            for count_columns in range(numRows):
                if i < n:
                    s_Initialize[count_columns] += s[i]  # 这里进行了将numRows个字符从上往下安置入每一行
                    # print(s_row)
                    i += 1
            # print(s_row)
            for count_Rows in range(numRows - 2, 0, -1):  # 这里进行了将numRows-2个字符从下往上安置入每一行
                if i < n:
                    s_Initialize[count_Rows] += s[i]
                    i += 1
        return ''.join(s_Initialize)

Leetcode12 整数转罗马数字

class Solution:
    def intToRoman(self, num: int) -> str:
        nums = [1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1]
        romans = ["M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"]

        index = 0
        res = ''
        while index < 13:
            # 注意：这里是等于号，表示尽量使用大的"面值"
            while num >= nums[index]:
                res += romans[index]
                num -= nums[index]
            index += 1
        return res

Leetcode17 电话号码的字母组合

Golang实现

func letterCombinations(digits string) []string {
	hash := map[rune][]string{
		'2': {"a", "b", "c"},
		'3': {"d", "e", "f"},
		'4': {"g", "h", "i"},
		'5': {"j", "k", "l"},
		'6': {"m", "n", "o"},
		'7': {"p", "q", "r", "s"},
		'8': {"t", "u", "v"},
		'9': {"w", "x", "y", "z"},
	}

	result := make([]string, 0)
	for _, v := range digits {
		if len(result) == 0 {
			result = hash[v]
		} else {
			tmp := make([]string, 0)
			for _, item := range result {
				for _, letter := range hash[v] {
					tmp = append(tmp, item+letter)
				}
				result = tmp
			}
		}
	}
	return result
}

Leetcode18 四数之和

golang实现

func kSum(num, target int, list []int) [][]int {
	result := make([][]int, 0)
	if num > len(list) {
		return result
	}
	if num == 2 {
		left := 0
		right := len(list) - 1
		for left < right {
			if list[left]+list[right] > target {
				right--
			} else if list[left]+list[right] < target {
				left++
			} else {
				item := []int{list[left], list[right]}
				result = append(result, item)
				left++
				right--
				for list[left] == list[left-1] && left+1 < len(list) {
					left++
				}
				for list[right] == list[right+1] && right-1 > 0 {
					right--
				}
			}
		}
	} else {
		for i, v := range list {
			if i-1 >= 0 && v == list[i-1] {
				continue
			}
			if i > len(list)-num {
				break
			}
			res := kSum(num-1, target-v, list[i+1:])
			for _, item := range res {
				result = append(result, append(item, v))
			}
		}
	}
	return result
}

func fourSum(nums []int, target int) [][]int {
	sort.Slice(nums, func(a, b int) bool {
		return nums[a] < nums[b]
	})
	return kSum(4, target, nums)
}

解析：
对于2数之和，我们可以采用双指针法，即一个在头一个在尾部
left = 0, right = n - 1
如果 nums[left] + nums[right] > target 那么right减一
如果 nums[left] + nums[right] < target 那么left加一
通过这样，最后找到 nums[left] + nums[right] == target， 就加入到结果列表中
为了找到所有符合的，还要继续 left++,right–继续查找
但是要记得去重：left++之后要保证 nums[left] != nums[left-1]，对于right也是同理

对于k数之和
其实就是递归来实现，直到变成 2数之和
递归方式是，对列表元素进行循环
取出其中一个数c，剩下的去做 k-1个数之和，target为target-c
记得这一步也要去重，要保证取出的数c，不能已经取过

这个办法要求先排序

Leetcode19

很简单，一个进行删除操作的指针 + 一个探测到达末尾的指针即可

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func removeNthFromEnd(head *ListNode, n int) *ListNode {
    detect := head
    for i:=0; i<n;i++{
        detect = detect.Next
    }
    if detect == nil{
        return head.Next
    }
    p := head
    for detect.Next != nil{
        p = p.Next
        detect = detect.Next
    }
    p.Next = p.Next.Next
    return head
}

Leetcode22 括号生成

状态机递归法：
判断当前的状态可以加 左括号还是加右括号
然后递归去生成列表

重要的一点是如何制造终止条件

func statusMachine(n, left, right int, prefix string) []string {
	res := make([]string, 0)
	if left+right == 0 {
		return append(res, prefix)
	}
	status := (n - left) - (n - right)
	if status == 0 && left-1 > 0 {
		res = statusMachine(n, left-1, right, prefix+"(")
	} else if status >= 0 {
		if left-1 >= 0 {
			res = statusMachine(n, left-1, right, prefix+"(")
		}
		if right-1 >= 0 {
			res = append(res, statusMachine(n, left, right-1, prefix+")")...)
		}
	}
	return res
}

func generateParenthesis(n int) []string {
	return statusMachine(n, n, n, "")
}

Leetcode24 两两交换链表中的节点

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */

func swapPairs(head *ListNode) *ListNode {
    if head == nil{
        return nil
    }
	A := head
	B := head.Next
	pre := &ListNode{0, A}
	node := pre
	for A != nil && B != nil {
		store := B.Next
		B.Next = A
		A.Next = store
		pre.Next = B
		pre = A
		A = A.Next
		if B.Next != nil && B.Next.Next != nil {
			B = B.Next.Next.Next
		}
	}
	return node.Next
}

Leetcode29

本代码溢出处理直接用常量数去判断 2147483648

func divide(dividend int, divisor int) int {
	flag := 1
	if dividend < 0 {
		flag = 0 - flag
		dividend = 0 - dividend
	}
	if divisor < 0 {
		flag = 0 - flag
		divisor = 0 - divisor
	}
	i := 0
	sum := 0
	accelerator := divisor
	acceleratorNum := 1
	for sum < dividend {
		if sum+divisor > dividend {
			break
		}
		if sum+accelerator > dividend {
			accelerator = divisor
			acceleratorNum = 1
		} else if sum+accelerator <= dividend {
			sum = sum + accelerator
			i += acceleratorNum
			accelerator += divisor
			acceleratorNum += 1
		}
	}
	res := i
	if flag < 0 {
		res = 0 - i
	}
	if !(res >= -2147483648 && res <= 2147483647) {
		return 2147483647
	}
	return res
}

Leetcode31 下一个排列

class Solution(object):
    def nextPermutation(self, nums):
        num1=nums[::-1]
        a=num1[0]
        c=0
        list1=[]
        for b in num1:
            if b>a:
                list1.append(b)
                a=b
                c+=1
            elif b==a:
                list1.append(b)
                c+=1
            else:
                break
        d=len(nums)-c-1
        e=nums[d]
        g=0
        for f in range(len(list1)):
            if list1[f]>e:
                break
            else:
                g+=1
        h=len(nums)-g-1
        j=nums[h]
        nums[d]=j
        nums[h]=e
        list2=nums[d+1:]
        list2.sort()
        nums[d+1:]=list2
        return nums

Leetcode34 在排序数组中查找元素的第一个和最后一个位置

func searchRange(nums []int, target int) []int {
	if len(nums) == 0 {
		return []int{-1, -1}
	}

	left := 0
	right := len(nums) - 1
	begin := -1
	for left <= right {
		if nums[left] == target {
			begin = left
			break
		} else if nums[right] == target {
			begin = right
			break
		} else {
			mid := (left + right) / 2
			if mid == left || mid == right {
				break
			}
			if nums[mid] > target {
				right = mid
			} else {
				left = mid
			}
		}
	}
	if begin == -1 {
		return []int{-1, -1}
	}
	for begin-1 > 0 && nums[begin-1] == target {
		begin--
	}
	end := begin
	for end+1 < len(nums) && nums[end+1] == target {
		end++
	}
	return []int{begin, end}
}

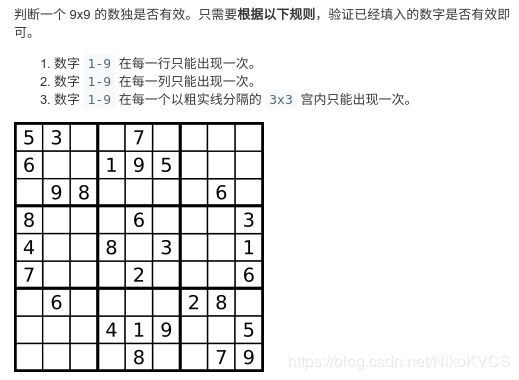
Leetcode36 有效的数独

样本数据

func isValidSudoku(board [][]byte) bool {

	for i := 0; i < 9; i++ {
		hash := make(map[byte]byte, 0)
		for j := 0; j < 9; j++ {
			if board[i][j] == byte('.') {
				continue
			}
			if _, ok := hash[board[i][j]]; ok {
				return false
			}
			hash[board[i][j]] = board[i][j]
		}
	}

	for j := 0; j < 9; j++ {
		hash := make(map[byte]byte, 0)
		for i := 0; i < 9; i++ {
			if board[i][j] == byte('.') {
				continue
			}
			if _, ok := hash[board[i][j]]; ok {
				return false
			}
			hash[board[i][j]] = board[i][j]
		}
	}

	for m := 0; m < 3; m++ {
		for n := 0; n < 3; n++ {
			hash := make(map[byte]byte, 0)
			for i := m * 3; i < m*3+3; i++ {
				for j := n * 3; j < n*3+3; j++ {
					if board[i][j] == byte('.') {
						continue
					}
					if _, ok := hash[board[i][j]]; ok {
						return false
					}
					hash[board[i][j]] = board[i][j]
				}
			}
		}
	}
	return true
}

Leetcode50

折半计算法

func myPow(x float64, n int) float64 {
	flag := 1
	if n < 0 {
		flag = -1
		n *= flag
	}
	res := 1.0
	for i := n; i != 0; i /= 2 {
		if i%2 != 0 {
			res *= x
		}
		x *= x
	}
	if flag == -1 {
		res = 1 / res
	}
	return res
}

Leetcode55 跳跃游戏

func canJump(nums []int) bool {
	dp := make([]int, len(nums))
	dp[0] = 1
	for i, v := range nums {
		if dp[i] == 0 {
			continue
		}
		for j := i; j <= i+v && j < len(nums); j++ {
			dp[j] = 1
		}
	}
	if dp[len(nums)-1] == 1 {
		return true
	} else {
		return false
	}
}