神经网络实现基本的与或异或逻辑
平时计算机领域的OR AND XOR逻辑问题就不去详说,大家都有学习过。
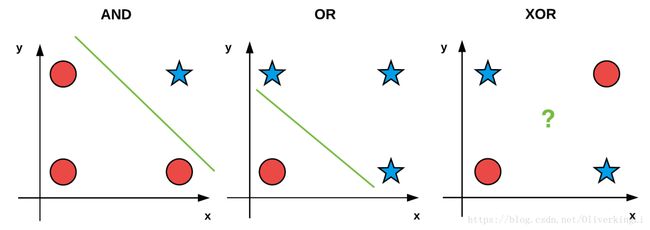
基本的逻辑图如下:
最开始神经网络解决线性可分问题给它带来了一次小高峰,但是在几年之后一个学者提出了XOR非线性问题的时候,并且专门写了一篇论文论述神经网络对非线性问题求解的无能为力直接给当年的神经网络的发展带来了寒冰时代。直到十几年后,多层网络的出现,也就是俗称的MLP(Multiply layer perceptron)才把Neural Network带来不断发展的时期。
我们知道OR或者AND都是线性可分,而XOR却是非线性可分的,用一幅图表示:
对于第三个坐标是无论如何也无法画出一条2维坐标上的直线把星星和圆圆直接分开的。
接下来我们使用最开始的神经网络代码来实现,也就是一个输入层,然后加上各自的权重后再总体加上偏置得到输出。
代码:
percetron.py
import numpy as np
class Perceptron:
def __init__(self, N, alpha=0.1):
self.W = np.random.randn(N + 1) / np.sqrt(N)
self.alpha = alpha
def step(self, x):
return 1 if x > 0 else 0
def fit(self, X, y, epochs=10):
X = np.c_[X, np.ones((X.shape[0]))]
for epoch in np.arange(0, epochs):
for (x, target) in zip(X, y):
p = self.step(np.dot(x, self.W))
if p != target:
error = p - target
self.W += -self.alpha * error * x
def predict(self, X, addBias=True):
X = np.atleast_2d(X)
if addBias:
X = np.c_[X, np.ones((X.shape[0]))]
return self.step(np.dot(X, self.W))
test.py
from perceptron import Perceptron
import numpy as np
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_or = np.array([[0], [1], [1], [1]])
y_and = np.array([[0], [0], [0], [1]])
y_xor = np.array([[1], [0], [0], [1]])
print("[INFO] training perceptron....")
p = Perceptron(X.shape[1], alpha=0.1)
p.fit(X, y_or, epochs=20)
print("[INFO] testing perceptron OR...")
for (x, target) in zip(X, y_or):
pred = p.predict(x)
print("[INFO] data={}, ground_truth={}, pred={}".format(x, target[0], pred))
print("[INFO] training perceptron AND....")
p = Perceptron(X.shape[1], alpha=0.1)
p.fit(X, y_and, epochs=20)
print("[INFO] testing perceptron AND...")
for (x, target) in zip(X, y_and):
pred = p.predict(x)
print("[INFO] data={}, ground_truth={}, pred={}".format(x, target[0], pred))
print("[INFO] training perceptron XOR....")
p = Perceptron(X.shape[1], alpha=0.1)
p.fit(X, y_xor, epochs=200)
print("[INFO] testing perceptron XOR...")
for (x, target) in zip(X, y_xor):
pred = p.predict(x)
print("[INFO] data={}, ground_truth={}, pred={}".format(x, target[0], pred))
print("X.shape\n", X.shape)
print("X.shape[0]\n", X.shape[0])
print("X.shape[1]\n", X.shape[1])
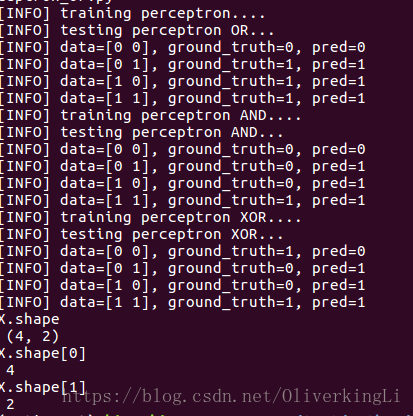
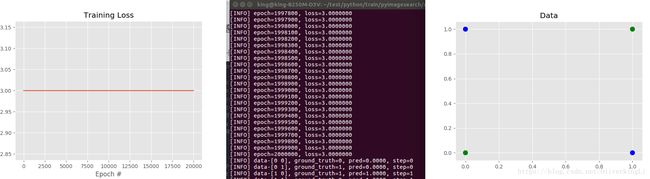
result:
可见对于XOR问题,没有隐藏层存在的情况下,神经网络基本学不到那种分类能力。然后我们改进网络,加入hidden layers,然后看能否解决问题,这里只加入一层的隐藏层。
neuralnetwork.py
import numpy as np
# 将完整的神经网络结构定义成类
class NeuralNetwork:
# 初始化,构造函数
def __init__(self, layers, alpha=0.1):
self.W = []
self.layers = layers
self.alpha = alpha
# 除了最后两层网络外,其他的都初始化Weight
for i in np.arange(0, len(layers) - 2):
# 先初始化常规的weights矩阵
w = np.random.randn(layers[i] + 1, layers[i+1] + 1)
# 归一化
self.W.append(w / np.sqrt(layers[i]))
# print("W without bias trick:\n", self.W)
# 使用bias trick也就是在W矩阵最后一列加入新的一列作为bias然后weight和bias合并为一个大W矩阵
# biases可以作为学习参数进行学习
w= np.random.randn(layers[-2] + 1, layers[-1])
# 归一化
self.W.append(w / np.sqrt(layers[-2]))
# print("W with bias trick:\n", self.W)
# 重载python的magic函数
def __repr__(self):
return "NeuralNetwork:{}".format("-".join(str(l) for l in self.layers))
def sigmoid(self, x):
return 1.0 / (1 + np.exp(-x))
# 对sigmoid函数求导
def sigmoid_deriv(self, x):
'''
y = 1.0 / (1 + np.exp(-x))
return y * (1 - y)
'''
return x * (1 - x)
def fit(self, X, y, epochs=1000, displayUpdate=100):
X = np.c_[X, np.ones((X.shape[0]))]
losses = []
# 根据每一层网络进行反向传播,然后更新W
for epoch in np.arange(0, epochs):
for (x, target) in zip(X, y):
self.fit_partial(x, target)
# 控制显示,并且加入loss
if epoch == 0 or (epoch + 1) % displayUpdate == 0:
loss = self.calculate_loss(X, y)
losses.append(loss)
print("[INFO] epoch={}, loss={:.7f}".format(epoch + 1, loss))
return losses
# 链式求导
def fit_partial(self, x, y):
A = [np.atleast_2d(x)]
for layer in np.arange(0, len(self.W)):
net = A[layer].dot(self.W[layer])
out = self.sigmoid(net)
A.append(out)
# backprogation algorithm
error = A[-1] - y
D = [error * self.sigmoid_deriv(A[-1])]
for layer in np.arange(len(A) - 2, 0, -1):
delta = D[-1].dot(self.W[layer].T)
delta = delta * self.sigmoid_deriv(A[layer])
D.append(delta)
D = D[::-1]
# 更新权值W
for layer in np.arange(0, len(self.W)):
self.W[layer] += -self.alpha * A[layer].T.dot(D[layer])
# 预测
def predict(self, X, addBias=True):
p = np.atleast_2d(X)
# 是否加入偏置
if addBias:
p = np.c_[p, np.ones((p.shape[0]))]
# 正常的前向传播得到预测的输出值
for layer in np.arange(0, len(self.W)):
p = self.sigmoid(np.dot(p, self.W[layer]))
return p
# 计算loss,就是计算MSE
def calculate_loss(self, X, targets):
targets = np.atleast_2d(targets)
predictions = self.predict(X, addBias=False)
loss = 0.5 * np.sum((predictions - targets) ** 2)
return loss
if __name__ == '__main__':
nn = NeuralNetwork([2, 2, 1])
print(nn)
test.py
from neuralnetwork import NeuralNetwork
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# 生成的数据
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_or = np.array([[0], [1], [1], [1]])
y_and = np.array([[0], [0], [0], [1]])
y_xor = np.array([[0], [1], [1], [0]])
# 构造2-2-1结构的神经网络,2个节点输入层,2个节点的隐藏层,1个节点的输出层
nn = NeuralNetwork([2, 2, 1], alpha=0.5)
# 模型开始训练,更新得到最终不断迭代更新的weigh矩阵
losses = nn.fit(X, y_xor, epochs=2000000)
# 打印输出
for (x, target) in zip(X, y_xor):
pred = nn.predict(x)[0][0]
step = 1 if pred > 0.5 else 0
print("[INFO] data-{}, ground_truth={}, pred={:.4f}, step={}"
.format(x, target[0], pred, step))
# 可视化训练过程
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
cm_dark = mpl.colors.ListedColormap(['g', 'b'])
plt.scatter(X[:, 0], X[:, 1], marker="o", c=y_xor.ravel(), cmap=cm_dark, s=80)
# print(testY)
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, len(losses)), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()
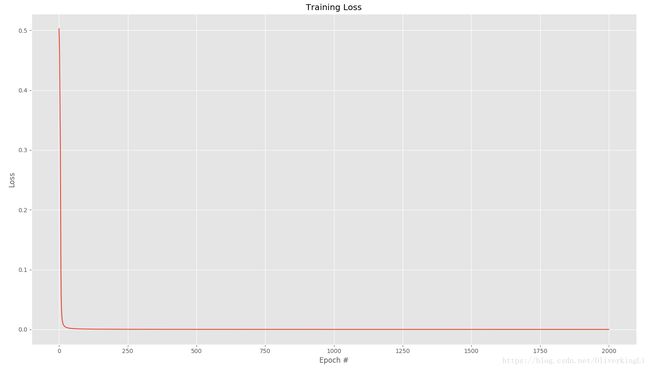
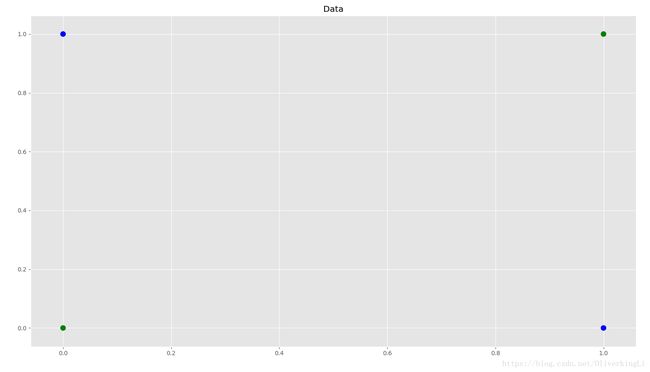
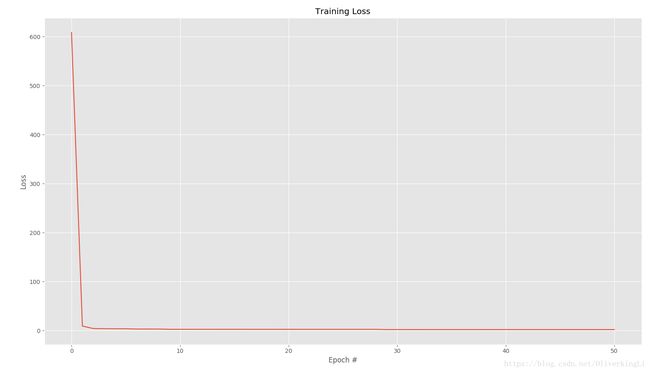
print("W\n", nn.W)result:
很好,可见加入一层hidden layer之后,可以很好解决非线性问题。
这里当然也可以把网络定义成之前的没有隐藏层的结构:
test.py
from neuralnetwork import NeuralNetwork
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# 生成的数据
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_or = np.array([[0], [1], [1], [1]])
y_and = np.array([[0], [0], [0], [1]])
y_xor = np.array([[0], [1], [1], [0]])
# 构造2-2-1结构的神经网络,2个节点输入层,2个节点的隐藏层,1个节点的输出层
nn = NeuralNetwork([2, 1], alpha=0.5)
# 模型开始训练,更新得到最终不断迭代更新的weigh矩阵
losses = nn.fit(X, y_xor, epochs=2000000)
# 打印输出
for (x, target) in zip(X, y_xor):
pred = nn.predict(x)[0][0]
step = 1 if pred > 0.5 else 0
print("[INFO] data-{}, ground_truth={}, pred={:.4f}, step={}"
.format(x, target[0], pred, step))
# 可视化训练过程
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
cm_dark = mpl.colors.ListedColormap(['g', 'b'])
plt.scatter(X[:, 0], X[:, 1], marker="o", c=y_xor.ravel(), cmap=cm_dark, s=80)
# print(testY)
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, len(losses)), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()
print("W\n", nn.W)result:
我们将这一MLP算法应用到MNIST数据集上看看:
testMNIST.py
from neuralnetwork import NeuralNetwork
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
# 从sklearn包中导入数据MNIST,其实是MNIST数据集的缩小版,仅包含1797张images
print("[INFO] loading mnist dataset...")
digits = datasets.load_digits()
data = digits.data.astype("float")
# print(data)
# 归一化到(0, 1)
data = (data - data.min()) / (data.max() - data.min())
print("[INFO] samples:{}, dim:{}".format(data.shape[0], data.shape[1]))
# print(data)
# 75%做训练数据集,25%做测试数据集
(trainX, testX, trainY, testY) = train_test_split(data, digits.target, test_size=0.25)
print("trainY:\n", trainY)
print("testY:\n", testY)
# 将标签值向量化,即是one-hot编码,如0--[1,0,0,0,0,0,0,0,0,0],1--[0,1,0,0,0,0,0,0,0,0],9--[0,0,0,0,0,0,0,0,0,1]
trainY = LabelBinarizer().fit_transform(trainY)
testY = LabelBinarizer().fit_transform(testY)
print("Vectorize trainY:\n", trainY)
print("trainY[0]\n", testY[0])
print("Vectroize testY:\n", testY)
# 定义网络结构64-32-32-16-10,64表示输入层有64个nodes(因为8x8=64),输出层有10个nodes(10个数值0-9输出)
print("[INFO] training network...")
nn = NeuralNetwork([trainX.shape[1], 32, 32, 16, 10])
print("[INFO] {}".format(nn))
# print("trainX.shape[0]:\n", trainX.shape[0])
# print("trainX.shape:\n", trainX.shape)
print("trainX.shape\n", trainX.shape)
print("testY.shape\n", testY.shape)
# 训练模型
losses = nn.fit(trainX, trainY, epochs=5000)
# 预测,并生成报告
print("[INFO] evaluating network...")
predictions = nn.predict(testX)
predictions = predictions.argmax(axis=1)
print(classification_report(testY.argmax(axis=1), predictions))
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, len(losses)), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()
print("W\n", nn.W)
result:
得到97%的平均准确率还是可以的。