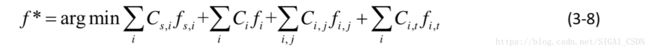视觉多目标跟踪算法综述(上)

 

1. 导言

目标跟踪是机器视觉中一类被广为研究的重要问题，分为单目标跟踪与多目标跟踪。前者跟踪视频画面中的单个目标，后者则同时跟踪视频画面中的多个目标，得到这些目标的运动轨迹。

基于视觉的目标自动跟踪在智能监控、动作与行为分析、自动驾驶等领域都有重要的应用。例如，在自动驾驶系统中，目标跟踪算法要对运动的车、行人、其他动物的运动进行跟踪，对它们在未来的位置、速度等信息作出预判。

目标跟踪算法可以进行轨迹特征的自动分析和提取，以弥补视觉目标检测的不足，有效的去除错误的检测，增加遗漏的检测，为进一步的行为分析提供基础。相对于多目标跟踪算法，视觉单目标跟踪算法研究的更为广泛，当前解决的相对更好。典型的如Mean shift算法，用卡尔曼滤波、粒子滤波进行状态预测，TLD等基于在线学习的跟踪，KCF等基于相关性滤波的算法等。

对于单目标跟踪算法的测试视频来说，存在一个先验假设是目标总是在摄像机视场范围内，因此即使把矩形框固定在初始位置，有时候仍然能得到一个看起来还好的跟踪结果(如图1)。

多目标跟踪问题没有上述的先验假设，一般情况下，多目标跟踪的对象位置变化很大，跟踪对象可以从场景入口进入，从出口离开，跟踪目标个数不固定。另外，多目标跟踪问题通常追踪给定类型的多个对象，同类对象具有一定的外观轮廓相似性，如下图跟踪场景：

相对来说，多目标跟踪问题更加复杂，除了单目标跟踪中存在的物体形变、背景干扰等因素。通常还需要解决以下一些问题：

• 跟踪目标的自动初始化和自动终止，即处理新目标的出现，老目标的消失

• 跟踪目标的运动预测和相似度判别，即准确的区分每一个目标

• 跟踪目标之间的交互和遮挡处理

• 跟丢目标再次出现时，如何进行再识别问题

多目标跟踪任务需要解决比单目标跟踪更多的问题和难点，如何有效地解决这些问题对多目标跟踪算法有重要意义。在这篇文章中，SIGAI将和大家一起对一些经典的视觉多目标跟踪算法进行回顾和归纳，以理解视觉多目标跟踪算法的框架和当前主流算法的框架和基本原理，如果对本文的观点持有不同的意见，欢迎向我们的公众号发消息一起讨论。

2. 视觉多目标跟踪算法的分类

多目标跟踪问题最早出现在雷达信号中目标运动轨迹的跟踪，如同时跟踪飞过来的多架敌人的飞机和多枚导弹。这些算法后来被借鉴用于机器视觉领域的多目标跟踪任务，随着计算机视觉领域的深入研究，近年来研究者对多目标跟踪算法从不同的方面进行了扩展。比如通过扩展单目标跟踪算法来支持多目标的情况，更多的工作从整个视频场景出发，对所有的目标轨迹做了统一的考虑。根据不同的分类标准，多目标跟踪算法有不同的分类方法。比如按照预测校正的跟踪和按照关联方式的跟踪，按照离线方式的关联跟踪和按照在线方式的跟踪，按照确定性推导的跟踪算法和按照概率统计最大化的跟踪等。

按照轨迹形成的时间顺序，多目标跟踪可以分为在线方式的跟踪算法以及离线形式的跟踪过程。如果跟踪的顺序是逐帧方式的：即为在线方式的目标跟踪方法。在线多目标跟踪与人眼实时跟踪目标过程类似，是对每个目标的状态进行估计，然后考虑整体状态的合理性进行约束。这个过程也可以简化为：获得每帧图像检测结果，把检测结果同已有的跟踪轨迹进行关联。如果跟踪算法运行是在视频已经获取结束，所有检测结果都已经提前获取情况下，这种跟踪方法为离线形式的多目标跟踪。离线多目标跟踪算法把检测结果集合作为观察，把轨迹看作检测集合的一种划分，因此跟踪问题转化为子集优化的过程。

按照跟踪算法形式化表示和优化框架过程，多目标跟踪可以分为确定性推导的跟踪和概率统计最大化的跟踪算法(如图3)。

在确定性推导的多目标跟踪框架中，我们把检测和轨迹和匹配看作为二元变量，通过构

造一个整体的目标函数，我们求变量的最佳值，使得目标函数最优，从而得到检测和轨迹的最佳匹配。这种整体的目标函数可以构造为二部图匹配的匹配代价，网络流的代价和，或者直接构造为机器学习中的分类问题进行优化计算。在概率统计最大化的多目标跟踪方法中，检测和轨迹的关系通过概率模型进行形式化，例如基于贝叶斯推导的卡尔曼滤波和粒子滤波，基于构造马尔科夫图模型，通过样本构造学习模型参数，在跟踪过程中计算概率最大化的轨迹结果，而对马尔科夫图模型的一个直接的公式化方法就是构造能量函数，因此能量最小化也是一些多目标跟踪算法常用的方式。

在一些情况下，这两种方法的区分不是非常明确的。比如机器学习算中，也可以采用统计学习方法进行建模，而能量最小化过程的推导实际是一个确定性的步骤。

上述对于多目标跟踪算法的分类，对于帮助理解不同的跟踪算法具有重要作用，而真正决定算法性能的可能并不是这些跟踪算法框架，而是一些更加基础的内容，比如如何构造检测结果的表观模型才能反应目标的特征，采用什么样的特征才能使得同一个目标更像，不同目标差异较大。又比如，如何判断检测结果是不是非常准确，如果不准确的话，特征匹配该如何计算匹配相似度。

对于特征表示的研究，目前广泛采用深度学习的方法，基于深度学习的多目标跟踪算法我们后续介绍。下面我们对经典的多目标跟踪算法进行概要的介绍。

 

3. 经典视觉多目标跟踪算法介绍

3.1 多假设多目标跟踪算法

多假设跟踪算法(MHT)是非常经典的多目标跟踪算法，由Reid在对雷达信号的自动跟踪研究中提出，本质上是基于Kalman滤波跟踪算法在多目标跟踪问题中的扩展。

定义在k时刻之前的检测为 (在更广泛的环境下也称为观测，如雷达扫描得到的目标的位置坐标、速度)，多假设跟踪的目标是基于已有轨迹对这种观测关联进行条件概率建模，把似然关联假设 划分为当前关联假设 (K)和k-1时刻的假设集合 。可以利用贝叶斯推理得到关于关联假设的后验概率公式：

其中公式右侧第一项表示基于前期假设集合和当前假设的观察似然概率，即在历史关联的基础上，当关联\vartheta_{I} (K)成立时，表现出当前观测Z(k)的概率；第二项表示当前假设的似然概率，即在历史关联的基础上，当前关联假设的概率；第三项表示前期假设集合后验概率。c是贝叶斯公式中的分母，对于当前观测已知的条件，可以认为是一个常数。从上式中可以看出，总体的假设后验概率可以表示为此三项的乘积。而公式第三项表示k-1时的后验概率，因此，只考虑第一项和第二项就可以得到一个递推公式。

如何对第一项和第二项进行建模？MHT采用了二个概率模型：

• 用均匀分布和高斯分布对关联对应的检测观察建模.

• 用泊松分布对当前假设的似然概率建模

前者表示，当观测是来自一个轨迹T时，它符合T的高斯分布，否则观测是一个均匀分布的噪声。后者表示，在误检和新对象出现概率确定的情况下，出现当前关联的可能性可以通过泊松分布和二项分布的乘积表示。在以上假设下，关联假设的后验分布是历史累计概率密度的连乘，转化为对数形式，可以看出总体后验概率的对数是每一步观察似然和关联假设似然的求和。因此，选择最佳的关联假设，转化为观察似然和关联假设似然累计求和的最大化。在进行具体实现和优化的时侯，I.J.Cox等人提出了一种基于假设树的优化算法，如图4所示。

图4: 左图为k-3时刻三个检测观察和两条轨迹的可能匹配。对于这种匹配关系，可以继续向前预测两帧，如图右。得到一种三层的假设树结构，对于假设树根枝干的剪枝，得到k-3时刻的最终关联结果。

对于k时刻的关联对数似然概率，可以认为是k时刻之前关联观察似然概率的对数求和，由于任何时刻都可能存在多种假设关联，因此到k时刻的假设构成了一种组合假设树的层次关系。例如图4左边表示的是2个轨迹和3个观测之间可能形成的关联假设，可能存在的假设有{观测23=>轨迹1，观测22=>轨迹2, 观测21=>新轨迹}或者{观测22=>轨迹1，观测21=>轨迹2, 观测23=>新轨迹}，因此产生2个假设分支。图4右侧是从这2个关联假设出发的三层假设树关系，可以看出随着假设层数的增多，关联假设出现组合爆炸的可能。因此进行必要的剪枝减少假设空间的数目是必须的步骤。那么如何选择最佳的关联呢？I.J.Cox采用了2个步骤来实现。首先，限制假设树的层数为3层。其次，是对每个分支的叶节点概率对数进行求和，最大的分支进行保留，即选择边缘概率最大的那个分支假设作为最后选择的关联。可以把这种选择方法简单的表示为：

采用基于均匀分布、泊松分布以及高斯分布的模型，可以高效快速计算选择k-3时优化的假设关联。这种基于似然概率对数累加的方法虽然方便迅速，但是存在一个主要的限制，即假定观测关联符合高斯模型，并且在每一步选择关联假设之后，需要利用Kalman滤波更新轨迹状态。通过对MHT基本公式(3-1)的扩展，可以建立不同的概率模型描述这种多假设关联的全局概率，例如Kim等人在ICCV2015和ECCV2018通过归一化的最小均方差优化算法引入表观模型来扩展MHT算法，取得不错的多行人跟踪结果[2,3]。

3.2 基于检测可信度的粒子滤波算法

如果不限定检测观测为高斯分布，一种采用概率统计的多目标跟踪框架是基于检测可信度的粒子滤波算法[4]。

这个算法分为两个步骤：

• 对每一帧的检测结果，利用贪心匹配算法与已有的对象轨迹进行关联。

• 利用关联结果，计算每个对象的粒子群权重，作为粒子滤波框架中的观察似然概率。

整体的跟踪过程采用粒子滤波框架，如图5中所示。

图5: 基于检测匹配的联合粒子滤波多目标跟踪算法流程对于每一帧的检测结果(图左)。可以计算与轨迹的匹配矩阵，本方法采用结合匹配结果设计粒子滤波算法(图中)，计算跟踪结果(图右)。

下面我们详细说明这两步:

第一步：利用贪心匹配算法关联当前帧检测和已有的对象轨迹。匹配亲和度计算如下：

其中tr表示一个轨迹，d是某一个检测，他们的匹配亲和度计算包含三个部分：在线更新的分类学习模型 (d)，用来判断检测结果是不是属于轨迹tr; 轨迹的每个粒子与检测的匹配度，采用中心距离的高斯密度函数求和 (d-p)表示；与检测尺寸大小相关的阈值函数g(tr,d)，表示检测与轨迹尺度的符合程度, 而α是预设的一个超参数。

计算出匹配亲和度矩阵之后，可以采用二部图匹配的Hungarian算法计算匹配结果。不过作者采用了近似的贪心匹配算法，即首先找到亲和度最大的那个匹配，然后删除这个亲和度，寻找下一个匹配，依次类推。贪心匹配算法复杂度是线性，大部分情况下，也能得到最优匹配结果。

第二步：采用粒子滤波框架，计算每个跟踪对象的粒子权重，计算公式如下：

其中tr表示需要跟踪的对象轨迹，p是某个粒子。指示函数I(tr)表示第一步关联中，轨迹tr是不是关联到某个检测结果，当存在关联时，计算与关联的检测d*的高斯密度P_{n}(p-d*)；C_{tr}(p)是对这个粒子的分类概率； (p)是粒子通过检测算法得到的检测可信度， (tr)是一个加权函数，计算如下：

当轨迹tr有检测匹配时，p_{o}(tr)为1；否则，他的附近有轨迹对象匹配成功时，取邻域轨迹的最大匹配高斯密度；如果附近也没有轨迹对象成功匹配，则p_{o}(tr)为0。

结合检测可信度的粒子滤波算法对轨迹的初始化采用了感兴趣区域的简单启发式策略。即，进入图像区域边框时，初始化对象；当连续多帧没有关联到检测时终止跟踪。在一些典型数据集上，基于检测可信度的粒子滤波算法可以得到不错的结果，如下表：

表1: 基于检测可信度粒子滤波的跟踪结果，采用CLEAR MOT评测标准进行结果评估

3.3 基于最小代价流优化的多目标跟踪算法

上述两个算法是基于贝叶斯概率模型的在线多目标跟踪算法。与他们不同，采用最小代价流优化的多目标跟踪算法是基于确定性优化的离线多目标跟踪算法[6]。

定义某条轨迹为 ，则需要求解最优化的是轨迹集合为T,T={T_{i}}。表示所有的检测集合为X,X={ }。离线全局最优化多目标跟踪问题实际可以表示为已知检测集合，求轨迹集合，按照贝叶斯推理，可以有：

考虑T={T_{i}}，按照每个轨迹对上式进行变换，并求对数得到：

上式中，右侧第一项表示轨迹的存在概率对数，第二项表示为在轨迹存在的条件下，检测是真的概率，把每条轨迹展开为检测的链接表示，那么上式可以表示为：

这里新的变量为{ }，他们与轨迹集合T的对应关系是：

由于满足链接只返生在不同检测和同一条轨迹之间，并且轨迹之间互斥，因此满足关系：

仔细观察发现，这里所求解的实际上网络流优化问题中满足代价最小的多个流，如图6。

图6: 最小代价流描述的检测划分方法，以产生全局最优的多目标跟踪算法。图中表示三帧图像中,分别有2, 4, 3个检测结果时，所产生的网络最小代价流[6]。

这里还有两个问题，网络流中边的代价怎么计算以及轨迹的数目怎么确定。

第一个问题，边的代价根据跟踪中轨迹生成概率、终止概率、相似概率、误检率计算：

第二个问题，轨迹数目通过迭代比较的方法确定。注意到检测节点代价Ci的值是一个负数，所以轨迹对应的网络流代价也可能小于0。因此，通过遍历不同轨迹数目，可以确定一个全局代价最小的解。这种方式带来算法的低效率，后续很多工作做了相关优化[7, 8]。

3.4 基于马尔科夫决策的多目标跟踪算法

不同于之前基于概率模型的在线多目标跟踪算法，Xiang等人采用了马尔科夫决策过程来推导每个轨迹的生成，称为MDP跟踪算法[9]。这是一种基于机器学习的确定性推导在线目标跟踪算法。

作者把目标跟踪看作为状态转移的过程，如图7。转移的过程用马尔科夫决策过程(MDP)建模。一个马尔科夫决策过程包括下面四个元素：(S, A, T(.)，R(.))。其中S表示状态集合，A表示动作集合，T表示状态转移集合，R表示奖励函数集合。一个决策是指根据状态s确定动作a, 即 π: S↦A。一个对象的跟踪过程包括如下决策过程：

• 从Active状态转移到Tracked或者Inactive状态：即判断新出现的对象是否是真。

• 从Tracked状态转移到Tracked或者Lost状态：即判断对象是否是持续跟踪或者暂时处于丢失状态。

• 从Lost状态转移到Lost或者Tracked或者Inactive状态：即判断丢失对象是否重新被跟踪，被终止，或者继续处于丢失状态。

作者设计了三个奖励函数来对上述三种决策进行建模：

第一个奖励函数是：

即判断新出现的对象是否为真，y(a)=1时表示转移到跟踪状态，反之转移到终止状态。这是一个二分类问题，采用2类SVM模型学习得到。这里用了5维特征向量：包括x-y坐标、宽、高和检测的分数。

第二个奖励函数是：

这个函数用来判断跟踪对象下一时刻状态是否是出于继续跟踪，还是处于丢失，即跟踪失败。这里作者用了5个历史模板，每个模板和当前图像块做光流匹配，emedFB表示光流中心偏差， 表示平均重合率。 和 是阈值。

第三个奖励函数是：

这个函数用来判断丢失对象是否重新跟踪，或者终止，或者保持丢失状态不变。这里当丢失状态连续保持超过 (=50)时，则转向终止，其他情况下通过计算M个检测匹配，来判断是否存在最优的匹配使上式(3-14)奖励最大，并大于0。这里涉及两个问题如何设计特征以及如何学习参数。这里作者构造了12维与模板匹配相关的统计值。而参数的学习采用强化学习过程，主要思想是在犯错时候更新二类分类器值。

表2中是本算法和其他算法在MOT2015测试数据集中运行结果比较，相对其他经典在线跟踪算法，MDP算法具有一定的优势。

表2: 采用马尔科夫决策过程的多目标在线跟踪算法在MOT2015中的评测结果

3.5 基于局部流特征的近似在线多目标跟踪算法

上面介绍的基于马尔科夫决策的在线多目标跟踪是对于当前帧的图像和检测结果，进行即时的轨迹状态更新。在另一类在线跟踪方法中，跟踪状态的最终结果与当前帧有一个小的帧差，这种方法称为近似在线多目标跟踪算法，MHT算法实际就是一种近似在线多目标跟踪算法。这里介绍的NOMT跟踪算法，是采用能量函数最小化设计的近似在线跟踪，对比MHT算法，没有高斯分布的假设，因此应用范围更广泛一些。 NOMT算法的主要思想是，对于当前时刻t,往回看