模拟退火算法(附python代码)
https://www.cnblogs.com/ranjiewen/p/6084052.html这篇文章把模拟退火的来龙去脉讲得十分清楚,下面直接上代码。值得注意的是对于不同的问题,其中的关键一步随机扰动的选择是不一样的,如果选择不当会导致搜索域变小或者很难达到最优解(较优),并且求得的解不一定就是最优解。
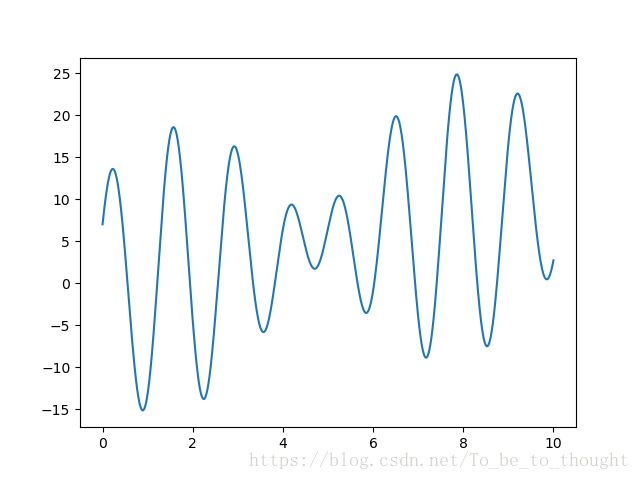
Q1:第一个例子就是求一个一元函数y=x+10sin(5x)+7cos(4x)的最小值:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import math
import random
from mpl_toolkits.mplot3d import Axes3D
#曲线显示
x = np.linspace(0,10,10000)
y = x+10*np.sin(5*x)+7*np.cos(4*x)
plt.plot(x,y)图像如图:
模拟退火算法的关键两个函数就是判断函数和随机扰动函数的编码,其中判断函数要根据优化目标进行符号调整,而随机扰动函数要考虑问题的维度或者复杂度。
#判断函数
#返回1表示接受当前解,返回0表示拒绝当前
#当系统内能减少时(目标函数值减小,新解更理想),接收该解;
#当系统内能增加时(新解比旧解更差),以一定的概率接受当前解(当T变小时,probability在减小,于是接受更差的解的概率值越小,退火过程趋于稳定)
def Judge(deltaE,T):
if deltaE < 0:
return 1
else:
probability = math.exp(-deltaE/T)
if probability > random.random():
return 1
else:
return 0这个问题的随机扰动函数就是让x在定义域内左右摆动(随机化):
#为当前解添加随机扰动
def Disturbance(low,high,x_old):
if random.random()>0.5:
x_new = x_old + (high - x_old) * random.random()
else:
x_new = x_old - (x_old - low) * random.random()
return x_new当然目标函数不能忘:
#优化目标函数
def ObjFun(x):
y = x + 10 * math.sin(5 * x) + 7 * math.cos(4 * x)
return y迭代循环过程如下:
#参数设置
low = 0
high = 9
tmp = 1e5
tmp_min = 1e-3
alpha = 0.98
#初始化
x_old = (high-low) * random.random() + low
x_new = x_old
value_old = ObjFun(x_old)
value_new = value_old
counter = 0
record_x = []
record_y = []
while(tmp > tmp_min and counter <= 10000):
x_new = Disturbance(low,high,x_old)
value_new = ObjFun(x_new)
deltaE = value_new - value_old
if Judge(deltaE,tmp)==1:
value_old=value_new
record_x.append(x_new)
record_y.append(value_new)
x_old=x_new
if deltaE < 0:
tmp=tmp*alpha #deltaE < 0说明新解较为理想,继续沿着降温的方向寻找,减少跳出可能性;当温度减小,当前内能变化量的概率值会变小
else:
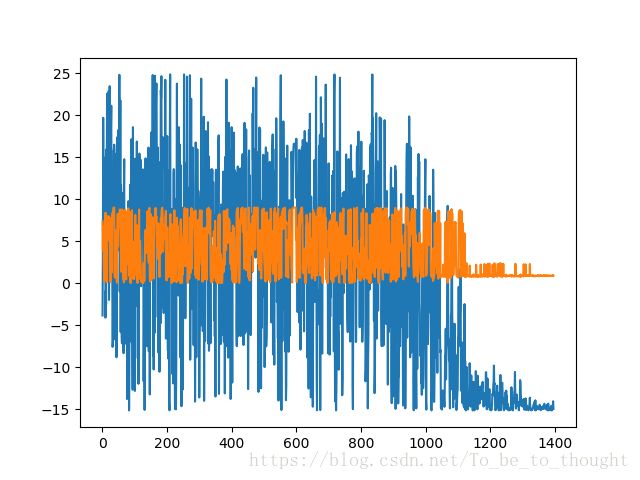
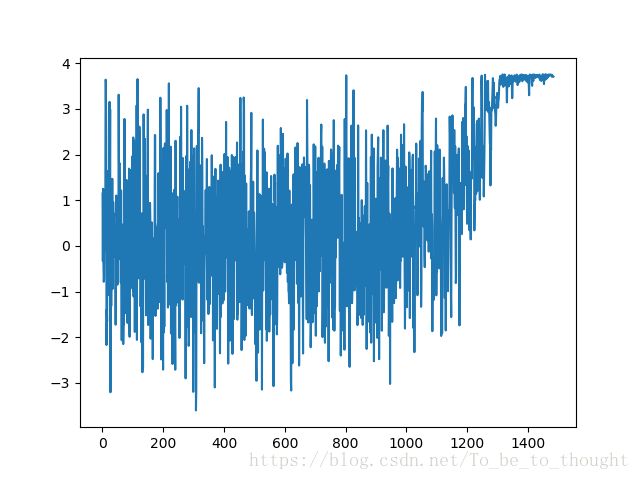
counter+=1迭代过程自变量x和函数值变化曲线如下,最终都收敛由于稳定值:
具体代码以及迭代动画如下:
#观察x的变化以及目标函数值的变化
length=len(record_x)
index=[i+1 for i in range(length)]
plt.plot(index,record_y)
plt.plot(index,record_x)
#动画绘制
fig, ax = plt.subplots()
l = ax.plot(x, y)
dot, = ax.plot([], [], 'ro')
def init():
ax.set_xlim(0, 10)
ax.set_ylim(-16, 25)
return l
def gen_dot():
for i in index:
newdot = [record_x[i-1], record_y[i-1]]
yield newdot
def update_dot(newd):
dot.set_data(newd[0], newd[1])
return dot,
ani = animation.FuncAnimation(fig, update_dot, frames = gen_dot, interval = 10, init_func=init)
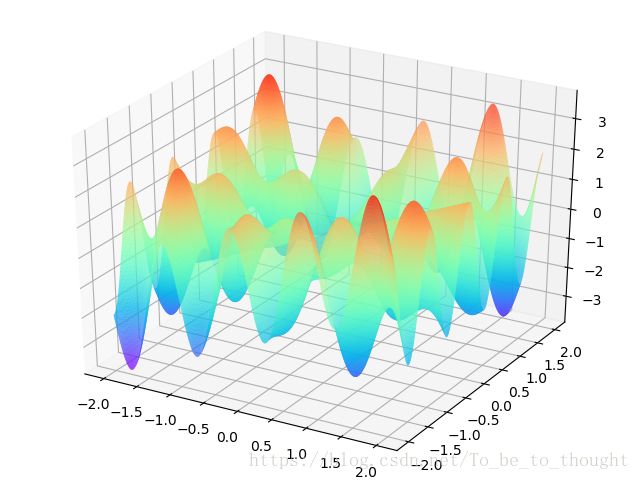
plt.show()Q2:求解二元函数y=ysin(2*pi*x)+xcos(2*pi*y)最大值
#三维曲面显示
X=np.linspace(-2,2,500)
Y=np.linspace(-2,2,500)
XX, YY = np.meshgrid(X, Y)
Z=YY*np.sin(2*math.pi*XX)+XX*np.cos(2*math.pi*YY)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(XX, YY, Z,rstride=1, cstride=1, cmap='rainbow')
plt.show()图像如下:
注意现在的扰动函数是在x和y方向上都会随机变化:
#待优化(最大值)目标函数
def ObjFunc(x,y):
z=y*math.sin(2*math.pi*x)+x*math.cos(2*math.pi*y)
return z
#给旧点以随机扰动
def Disturb(point_old,LB_POINT,RT_POINT):
if random.random()<0.5:
point_old[0]=LB_POINT[0]+random.random()*(point_old[0]-LB_POINT[0])
else:
point_old[0]=point_old[0]+random.random()*(RT_POINT[0]-point_old[0])
if random.random()<0.5:
point_old[1]=LB_POINT[1]+random.random()*(point_old[1]-LB_POINT[1])
else:
point_old[1]=point_old[1]+random.random()*(RT_POINT[1]-point_old[1])
return point_old[0],point_old[1]
def Judge2Max(deltaE,T):
if deltaE>0:
return 1
else:
probability=math.exp(deltaE/T)
if probability>random.random():
return 1
else:
return 0
LB_POINT = np.array([-2,-2])
RT_POINT=np.array([2,2])
x_old = 4*random.random()-2
y_old = 4*random.random()-2
x_new = x_old
y_new = y_old
point_old = np.array([x_old,y_old])
value_old = ObjFunc(x_old,y_old)
point_new = np.array([x_new,y_new])
value_new = value_old
tmp = 1e5
tmp_min = 1e-3
alpha = 0.98
counter = 0
record_coord = []
record_value = []
while(tmp >= tmp_min and counter <= 100000):
point_new[0],point_new[1] = Disturb(point_old,LB_POINT,RT_POINT)
value_new = ObjFunc(point_new[0],point_new[1])
deltaE = value_new - value_old
if Judge2Max(deltaE,tmp) == 1:
record_coord.append(point_new.copy())
record_value.append(value_new)
point_old = point_new
value_old = value_new
if deltaE > 0:
tmp = tmp * alpha
else:
counter += 1
print(counter)
length=len(record_value)
x=[i+1 for i in range(length)]
plt.plot(x,record_value)
coor_x=[record_coord[i][0] for i in range(length)]
coor_y=[record_coord[i][1] for i in range(length)]
coordinates=[]
for i in range(length):
coordinates.append([coor_x[0],coor_y[1]])
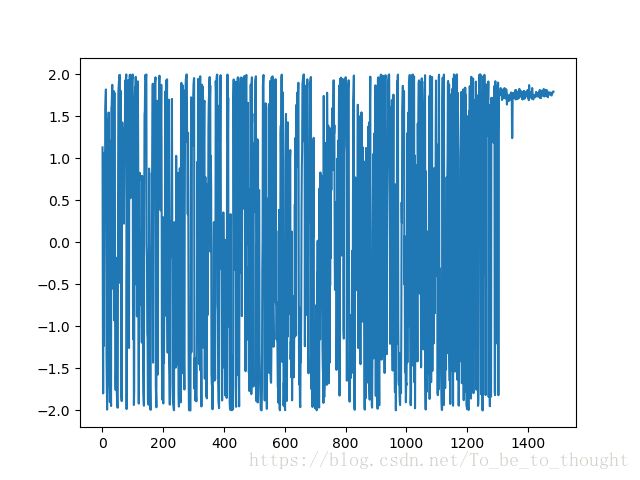
plt.plot(x,coor_x)
plt.plot(x,coor_y)横坐标x和纵坐标y以及函数值的变化曲线如下:
Q3.经典的TSP问题
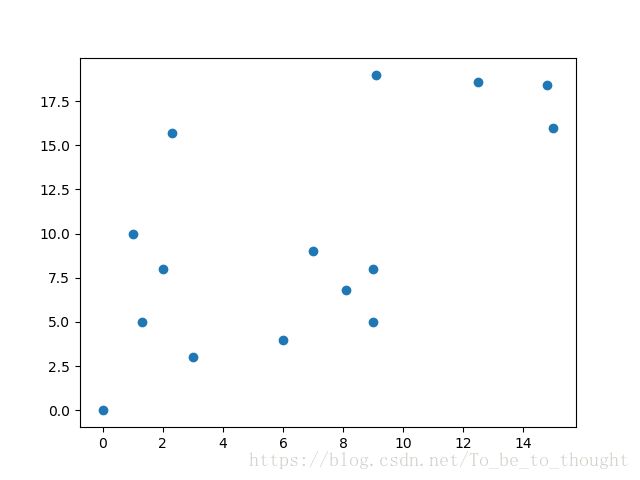
假设有这些城市,坐标如下:
cities_coords = np.array([[0,0],[1,10],[2,8],[9,5],[1.3,5],[7,9],[3,3],[6,4],[9,8],[8.1,6.8],[15,16],[12.5,18.6],[14.8,18.4],[2.3,15.7],[9.1,19]])图示:
随机扰动函数要做的就是将随机的两个城市交换位置,其他代码类似:
def Route_Length(cities):
s = 0
for i in range(cities.shape[0]-1):
s += math.sqrt(np.sum(np.power(cities[i+1,:]-cities[i,:],2)))
return s
#这里的扰动函数将随机将两个点位坐标的位置进行原地交换
def Exchange(cities):
n = cities.shape[0]
i = 0
j = 0
while True:
i = math.floor(random.random()*n)
j = math.floor(random.random()*n)
if i != j:
break
cities[[i,j],:] = cities[[j,i],:]
print("exchange " + str(i) + " and " + str(j))
return cities
def Judge(deltaE,T):
if deltaE < 0:
return 1
else:
probability = math.exp(-deltaE/T)
if probability > random.random():
return 1
else:
return 0
cities_old = cities_coords.copy()
length_old = Route_Length(cities_old)
cities_new = cities_coords.copy()
length_new = length_old
tmp = 1e5
tmp_min = 1e-5
alpha = 0.99
counter = 0
record_route = []
record_length = []
All_length = []
All_length.append(length_old)
while(tmp >= tmp_min and counter <= 1000000):
cities_new = Exchange(cities_old)
length_new = Route_Length(cities_new)
All_length.append(length_new)
deltaE = length_new - length_old
if Judge(deltaE,tmp) == 1:
record_route.append(cities_new.copy())
record_length.append(length_new)
cities_old = cities_new
length_old = length_new
print("第%d条线路的长度为:%0.2f" %(counter,record_length[-1]))
print(str(counter)+"次迭代的路线总长度"+str(length_old))
if deltaE < 0:
tmp = tmp * alpha
else:
counter += 1执行结果如下:
具体路线如下,显然不是最优解只是个较优解: