洛谷比赛 waaadreamer的圣诞虐题赛题解
比赛链接
本题解同步于洛谷博客
获奖名单
前三:
rank1:@GZY_GZY
rank2:@ljc1301
rank3:@加藤惠
orz三位dalao!tql!
一血榜:
A: @ThinkofBlank(09:05:39)
B: @muller(09:08:57)
C: @GZY_GZY(11:34:05)
D: @东师附中大头(10:57:32)
E: @GZY_GZY(18:29:35获得最高分58pts)
吐槽
谁知道我元旦想放水题放出锅了啊……T2据说是和别人差不多的题……对此我深表歉意。(既然这是基本全场AC的签到题大家就放我一马吧,感激不尽2333)
其它题应该没啥问题。
总体评估
T1,T2简单题,T3,T4稍有难度,T5较难(可能不太准?)部分分放的真的好多好多啊……
好了废话不多说,放题解。
T1 WD与矩阵
subtask1:
暴力即可。复杂度 O ( T 2 n m ) O(T2^{nm}) O(T2nm)。
subtask2:
这个部分分是脑子一抽给的,肯定没人写。直接枚举列,把行的状态状压起来就行。复杂度 O ( T m 2 2 n ) O(Tm2^{2n}) O(Tm22n)。
subtask3:
打表应该都能发现,答案就是 2 ( n − 1 ) ( m − 1 ) 2^{(n-1)(m-1)} 2(n−1)(m−1),因为我们可以最后一行和最后一列完全可以根据前面填的值直接算出来,因此任意排列前面的东西即可。复杂度 O ( T l o g n ) O(Tlogn) O(Tlogn)。
#include T2 WD与循环
subtask1:
我们会显然的发现问题转化为求有多少种不同的值使 ∑ i = 1 n a i ≤ m \sum_{i=1}^na_i\le m ∑i=1nai≤m。因此这个直接dp即可。
f [ i ] [ j ] f[i][j] f[i][j]表示当前到第 i i i个循环,前面值的和为 j j j的方案数,最后就是 ∑ i = 0 m f [ n ] [ i ] \sum_{i=0}^mf[n][i] ∑i=0mf[n][i],复杂度 O ( n m + T ) O(nm+T) O(nm+T).
subtask2:
发现有不等号不太方便,考虑如果是等号怎么做。这是显然的插板法(如果不知道可以度娘……),也就是说 ∑ i = 1 n a i = m \sum_{i=1}^na_i=m ∑i=1nai=m的非负解共有 ( n + m − 1 n − 1 ) \binom{n+m-1}{n-1} (n−1n+m−1)组,因为我们可以视为在 m m m个数中加上 n − 1 n-1 n−1个可相邻的隔板,相邻两个隔板之间的长度就代表了对应的数字。
因此我们预处理阶乘,直接枚举 m m m计算对应的组合数,然后求和即可。复杂度 O ( T m + m o d ) O(Tm+mod) O(Tm+mod)。
subtask3:
有个结论,就是:
∑ i = q n ( i q ) = ( n + 1 q + 1 ) \sum_{i=q}^n \binom{i}{q}=\binom{n+1}{q+1} i=q∑n(qi)=(q+1n+1)
简略证明如下:
∑ i = q n ( i q ) = ( n q ) + ( n q + 1 ) 即 ∑ i = q n − 1 ( i q ) = ( n q + 1 ) \sum_{i=q}^n\binom{i}{q}=\binom{n}{q}+\binom{n}{q+1}即\sum_{i=q}^{n-1}\binom{i}{q}=\binom{n}{q+1} i=q∑n(qi)=(qn)+(q+1n)即i=q∑n−1(qi)=(q+1n)
归纳即可。
因此原题的答案直接就是 ( n + m m ) \binom{n+m}{m} (mn+m),直接上卢卡斯定理即可。复杂度 O ( T + m o d ) O(T+mod) O(T+mod)。(假定卢卡斯求组合数为 O ( 1 ) O(1) O(1))。
#include T3 WD与数列
subtask1:
似乎 O ( n 3 ) O(n^3) O(n3)暴力直接可以把subtask2艹过去?luogu还是太快了啊!这个应该不用多说吧,直接暴力枚举一对开头,然后暴力向后扩展直到相减的值改变了。
subtask2:
本来这个点是给hash的……又怕hash常数大被卡,于是就只有1000的数据量……不管不管送分大甩卖!
(我看你是送分大甩锅吧2333)
首先可以想到差分整个序列,然后问题转化为求不相交不相邻的相等子串对数。
就是枚举答案的长度,然后从左往右跑,对于某个串,把他左边和他不相交或相邻的串的hash加到hash_map里,直接看有多少串的hash和它相同即可。复杂度 O ( n 2 ) O(n^2) O(n2)。
subtask3:
嘿嘿嘿这个点没法水过去了吧……
做法1: 肯定还是差分整个数列,接下来考虑怎么做。如果去掉不相交不相邻的这个限制直接SA+单调栈即可(或者SAM,但是慢啊)。接下来考虑如何把多算的减掉。
我们会发现多算的一定靠的很近(废话),可以考虑使用NOI2016优秀的拆分那题的方法,也就是使用调和级数。
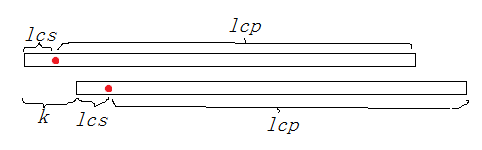
我们考虑枚举两个串的偏移位置(即图中的 k k k),然后每 k k k位打一个点,可以发现我们只需要让这两个串在它们第一次出现红点的位置被计算一次即可。
考虑计算两个红点为结尾的LCS和为开头的LCP,由于我们要让每对串只能在第一个红点处被计算,因此LCS要和 k k k取个min。然后就是细节功底了……考虑暴力怎么做,我们可以枚举两个串的开头位置 a , a + k a,a+k a,a+k,并且由于两个串要相邻或相交,则第一个串的结尾 b ≥ a + k − 1 b\ge a+k-1 b≥a+k−1。于是会发现最后实际上是计算一个等差数列求和的东西,就可以 O ( 1 ) O(1) O(1)算了。注意边界即可。
因此总复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),LCP和LCS可以用st表 O ( 1 ) O(1) O(1)算。常数比较大2333……
#include 做法2: 我们考虑差分完数列后建出后缀自动机。我们让两个相等且不相交的串在它们的右端点处被统计,于是沿parent树向上线段树合并出每个节点的right集,同时利用启发式合并计算出一个节点对另一个节点的贡献,这个可以直接线段树查询位置和。总复杂度 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n),但由于线段树/启发式合并常数小+不好卡,可以很快地通过此题。
这里放上@GZY_GZY 的代码。
// luogu-judger-enable-o2
#includeT4 WD与积木
subtask1:
显然可以dp。由于等概率下期望=总和/方案数,我们令 f [ i ] f[i] f[i]表示有 i i i个积木时产生层数的总和, g [ i ] g[i] g[i]表示 i i i个积木产生不同堆法的数量,则答案就是 f [ n ] g [ n ] \frac{f[n]}{g[n]} g[n]f[n]。显然,我们通过枚举第一层是哪些积木就可以dp了:
f [ n ] = g [ n ] + ∑ i = 1 n ( n i ) f [ n − i ] , f [ 0 ] = 0 f[n]=g[n]+\sum_{i=1}^n\binom nif[n-i],f[0]=0 f[n]=g[n]+i=1∑n(in)f[n−i],f[0]=0
g [ n ] = ∑ i = 1 n ( n i ) g [ n − i ] , g [ 0 ] = 1 g[n]=\sum_{i=1}^n\binom nig[n-i],g[0]=1 g[n]=i=1∑n(in)g[n−i],g[0]=1
复杂度 O ( n 2 ) O(n^2) O(n2)。
subtask2:
我们考虑答案的组合意义。实际上是把这些积木划分成了一些集合,然后任意排列这些集合求方案数和总和。
也就是说我们实际上求的是这个东西:
s u m = ∑ i = 1 n S ( n , i ) ⋅ i ! ⋅ i , c n t = ∑ i = 1 n S ( n , i ) ⋅ i ! , 那 么 答 案 = s u m c n t sum=\sum_{i=1}^nS(n,i)\cdot i!\cdot i,cnt=\sum_{i=1}^nS(n,i)\cdot i!,那么答案=\frac{sum}{cnt} sum=i=1∑nS(n,i)⋅i!⋅i,cnt=i=1∑nS(n,i)⋅i!,那么答案=cntsum
S ( n , i ) S(n,i) S(n,i)是第二类斯特林数。因此直接NTT预处理第二类斯特林数即可,复杂度 O ( T n l o g n ) O(Tnlogn) O(Tnlogn)。
subtask3:
考虑如何优化subtask1中的dp做法。不妨设:
F ( x ) = ∑ i f [ i ] i ! x i , G ( x ) = ∑ i g [ i ] i ! x i , H ( x ) = ∑ i x i i ! F(x)=\sum_i\frac{f[i]}{i!}x^i,G(x)=\sum_i\frac{g[i]}{i!}x^i,H(x)=\sum_i\frac{x^i}{i!} F(x)=i∑i!f[i]xi,G(x)=i∑i!g[i]xi,H(x)=i∑i!xi
则很容易得到 2 F ( x ) = G ( x ) + F ( x ) H ( x ) − 1 , 2 G ( x ) = G ( x ) H ( x ) + 1 2F(x)=G(x)+F(x)H(x)-1,2G(x)=G(x)H(x)+1 2F(x)=G(x)+F(x)H(x)−1,2G(x)=G(x)H(x)+1,不难解得:
F ( x ) = G ( x ) ( G ( x ) − 1 ) , G ( x ) = 1 2 − H ( x ) F(x)=G(x)(G(x)-1),G(x)=\frac{1}{2-H(x)} F(x)=G(x)(G(x)−1),G(x)=2−H(x)1
多项式求逆即可,复杂度 O ( n l o g n ) O(nlogn) O(nlogn)。
#include T5 WD与地图
subtask1:
显然,一个地区是原图的一个强连通分量,那么我们就在每次删除操作之后暴力跑一遍tarjan,然后对于每个强连通分量建立一颗权值线段树,节点记录权值的出现次数和节点上所有数字的和。每次修改就是把一个位置的出现次数-1,另一个位置+1;每次询问在线段树上二分一下就好了。复杂度 O ( Q l o g n + O(Qlogn+ O(Qlogn+删除次数 × m l o g n ) \times mlogn) ×mlogn).
subtask2:
把所有操作倒序,这样我们考虑如何维护加边操作后的强联通分量。比如连了一条a到b的边,可以暴力从b搜到a,沿途把所有点的权值线段树合并起来。这样做的复杂度是 O ( m × 删 除 次 数 + n l o g n + Q l o g n ) O(m\times 删除次数+nlogn+Qlogn) O(m×删除次数+nlogn+Qlogn)的,瓶颈在于暴力从b跑到a进行缩点。
subtask3:
做法2的瓶颈就在于无法快速求出每条边在什么时刻被缩起来的,这个东西的确不好直接用数据结构维护,我们可以考虑整体二分。
每次二分出一个 m i d mid mid,把出现时间小于等于 m i d mid mid的边全部加入到图里求一遍tarjan,就可以知道哪些边在 ≤ m i d \le mid ≤mid的时间内被缩掉了。具体的,我们还需要一个可撤销并查集来维护一下在当前有多少点已经被缩到一起,接下来就直接是整体二分的事情了。总复杂度 O ( Q l o g n ⋅ α ( n ) ) O(Qlogn\cdot\alpha(n)) O(Qlogn⋅α(n))。
#include