遗传算法与其python实现
遗传算法(Genetic Algorithm)和模拟退火算法一样,也是搜索启发式算法的一种,它是借鉴了自然界优胜劣汰与适者生存的思想,通过模拟自然界这一过程来搜索最优解,在机器学习、组合优化等方面有广泛的用途。
首先我们一样来看一个函数:
函数图像如下:
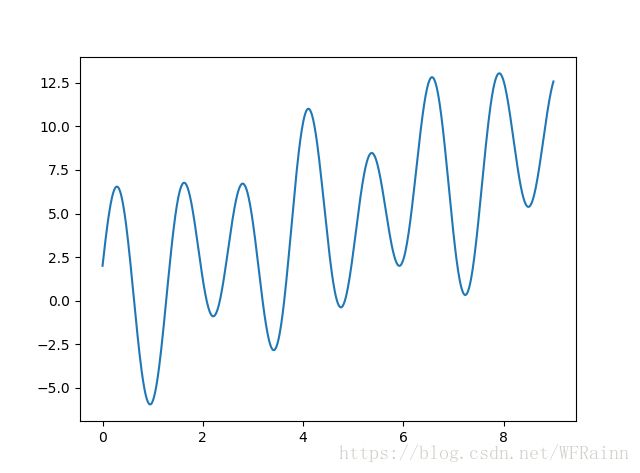
现在需要求这个函数在[0,9]的最大值并需要精确到4位小数。同样,如果使用穷举法,需要计算90000次。现在我们来看看如何用遗传算法优化求解过程。
1.遗传算法
遗传算法的组成主要包括4个部分:
(1)编码
(2)适应度函数
(3)遗传算子(选择,交叉,变异)
(4)运行参数
1.1编码与解码(code and decode)
实行遗传算法的首要任务是要确定编码与解码的形式,就如同生物遗传是通过染色体和基因进行一样。编码形式可以直接使用实数编码,也可以使用二进制编码,基本遗传算法(SGA)都是选取二进制编码。
现在,对于上面的问题,如何对90000个数进行二进制编码呢。我们考虑90000个数将自变量空间划分成了90000个等份,现在使用二进制来表示这90000个等份,由于:
那么,只需要17为二进制字符串便可以表达每一个等份,每一等份都对应一个不同的字符串。现在,如何将二进制字符串转化回原自变量呢?首先将二进制转化为十进制:
这样便可以清楚的进行解码了,如00000000000000000便代表0,而11111111111111111代表9。关于编码与解码的关系,还可以看作生物学中的基因型和表现型,二进制字符串就是基因型,而原自变量为表现型。
确定了编码与解码的方式,我们现在可以随机产生一群个体作为我们的初始种群。
1.2适应度函数(fitness function)
确定了初始种群后,我们如何判断种群中个体的好坏,也就是其生存下去的概率呢,这就是引入适应度函数的时候了。一般在实际问题中,适应度函数一般都是根据需要求解的函数来设定的。一般来说,适应度函数的值越高,则生存下去的几率越大。
1.3选择(selection)
接下来就要进行优胜劣汰的操作了,也就是选择,在遗传算法中,我们一般选择轮盘赌方法。

轮盘赌的主要思想为个体被选中的概率与其适应度函数的大小成比列,用公式表示概率为:
其中,n为个体总数,f(x)为适应度函数值。接下来进行轮盘赌选择:
在[0,1]之间随机生成一个数r,那么如果:
1. r<q1 r < q 1 ,则选择 x1 x 1
2. qi−1<r<qi q i − 1 < r < q i ,则选择 qi q i ,其中 2≤i≤n 2 ≤ i ≤ n 。
qi q i 被称为染色体i的累计概率,其公式为:
这样,通过轮盘赌,我们便可以选出跟适合现存生存法则下(适应度函数)更可能存活下去的个体。
1.4交叉(crossover)
交叉运算相当于生物中交配产生后代的行为。两个随机配对的个体按照一定的概率交换部分基因,从而形成两个新的个体。交叉算法是产生新个体的主要方法,也是遗传算法的关键部分。基本遗传算法一般采用单点交叉法。
假设现在有两个配对的个体如下:
现在假设其从第十位开始交换基因,则交换后产生的后代为:
这样,通过交叉算子,我们便得到了新一代个体。
1.5变异(mutation)
变异算子是模仿生物进化过程中的变异过程,即按照一定概率随机改变某些基因值,从而形成新的个体。它可以帮助算法跳出局部极值而有利于找到最优解。对于如下个体:
如果它的第十位产生了变异,那么将从原本的1变为0,新的个体如下:
一般来说,交叉的概率比较大,变异的概率很低。
1.6运行参数
介绍完所有的算子后,接下来我们便可以开始进行进化过程了。初始化种群个体数为m,进化次数为T,Pc为交叉概率,Pm为变异概率,那么每一轮进化将按照固定概率进行选择,交叉和变异。这样通过一代代进化,最终得到的个体将是适应度最大的一类,也就是我们想要的函数最优解。
2python实现
接下来我们便使用python实现遗传算法:
首先定义函数:
"""
Genetic Algorithm
"""
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
import math
def aimFunction(x):
y=x+5*math.sin(5*x)+2*math.cos(3*x)
return y
x=[i/100 for i in range(900)]
y=[0 for i in range(900)]
for i in range(900):
y[i]=aimFunction(x[i])
接着我们初始化种群,定义种群中个体数m=10:
population=[]
for i in range(10):
entity=''
for j in range(17):
entity=entity+str(np.random.randint(0,2))
population.append(entity)
然后我们在工具类中定义解码函数和适应度函数:
"""
utils.py
"""
from __future__ import division
def decode(x):
y=0+int(x,2)/(2**17-1)*9
return y
def fitness(population,aimFunction):
value=[]
for i in range(len(population)):
value.append(aimFunction(decode(population[i])))
#weed out negative value
if value[i]<0:
value[i]=0
return value1.这里int(x,2)可将x转化为十进制,2用于声明其为二进制。
2.这里因为适应度函数出现了负数。因为求的是最大值,所以我们直接将负数除去。
然后定义三个算子,首先是选择:
"""
selection.py
"""
from __future__ import division
import numpy as np
def selection(population,value):
#轮盘赌选择
fitness_sum=[]
for i in range(len(value)):
if i ==0:
fitness_sum.append(value[i])
else:
fitness_sum.append(fitness_sum[i-1]+value[i])
for i in range(len(fitness_sum)):
fitness_sum[i]/=sum(value)
#select new population
population_new=[]
for i in range(len(value)):
rand=np.random.uniform(0,1)
for j in range(len(value)):
if j==0:
if 0and rand<=fitness_sum[j]:
population_new.append(population[j])
else:
if fitness_sum[j-1]and rand<=fitness_sum[j]:
population_new.append(population[j])
return population_new 交叉算子:
"""
crossover.py
"""
from __future__ import division
import numpy as np
def crossover(population_new, pc):
half=int(len(population_new)/2)
father=population_new[:half]
mother=population_new[half:]
np.random.shuffle(father)
np.random.shuffle(mother)
offspring=[]
for i in range(half):
if np.random.uniform(0,1)<=pc:
copint = np.random.randint(0,int(len(father[i])/2))
son=father[i][:copint]+(mother[i][copint:])
daughter=mother[i][:copint]+(father[i][copint:])
else:
son=father[i]
daughter=mother[i]
offspring.append(son)
offspring.append(daughter)
return offspring
1.在进行配对时首先将原种群平分成两半并使用np.random.shuffle进行随机配对。
2.关于交叉基因个数的选择,这里我为了不让其交叉个数过多导致变化过大,将交叉基因数限制在总基因数一半以下。
最后是变异算子:
"""
mutation.py
"""
from __future__ import division
import numpy as np
def mutation(offspring,pm):
for i in range(len(offspring)):
if np.random.uniform(0,1)<=pm:
position=np.random.randint(0,len(offspring[i]))
#'str' object does not support item assignment,cannot use = to change value
if position!=0:
if offspring[i][position]=='1':
offspring[i]=offspring[i][:position-1]+'0'+offspring[i][position:]
else:
offspring[i]=offspring[i][:position-1]+'1'+offspring[i][position:]
else:
if offspring[i][position]=='1':
offspring[i]='0'+offspring[i][1:]
else:
offspring[i]='1'+offspring[i][1:]
return offspring这里在写的时候遇到了一个问题,最开始直接对字符串进行更改:offspring[i][j]='1',弹出错误提示'str' object does not support item assignment。后面发现字符串原来属于不可变量,这个应该就是基础没打牢的问题了。
定义完所有算子后,我们便可以开始进化过程了:
t=[]
for i in range(1000):
#selection
value=utils.fitness(population,aimFunction)
population_new=selection(population,value)
#crossover
offspring =crossover(population_new,0.7)
#mutation
population=mutation(offspring,0.02)
result=[]
for j in range(len(population)):
result.append(aimFunction(utils.decode(population[j])))
t.append(max(result))定义进化次数为1000次,交叉概率为0.7,变异概率为0.02,接着我们便运行进化过程,通过绘图来观察计算过程:
plt.plot(t)
plt.axhline(max(y), linewidth=1, color='r') 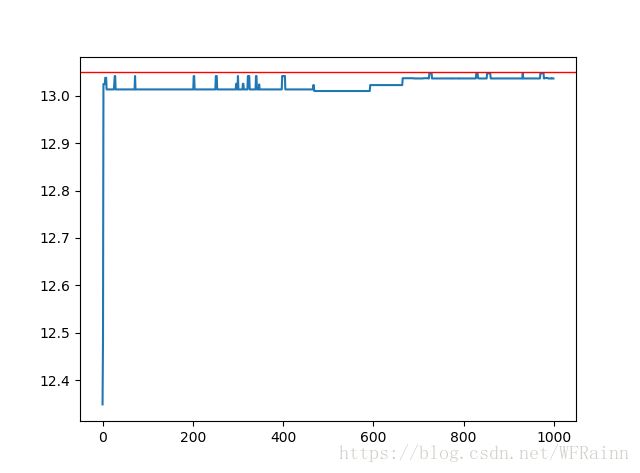
红线为其最大值,蓝线显示了遗传算法对最优解的逼近过程。
代码已上传至github:Genetic-Algorithm-with-python