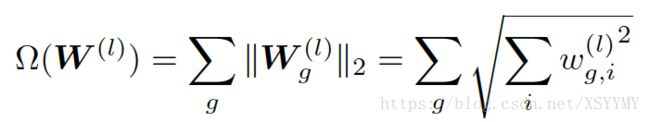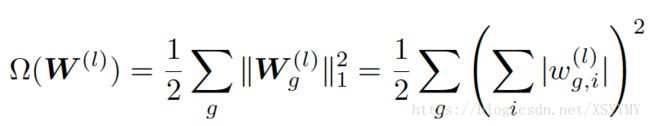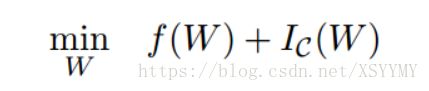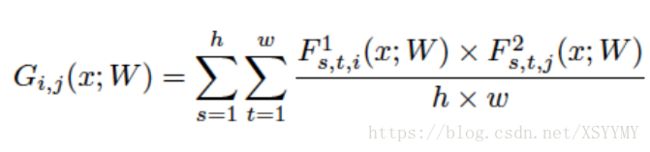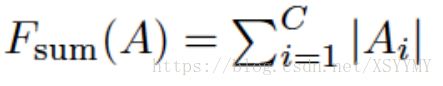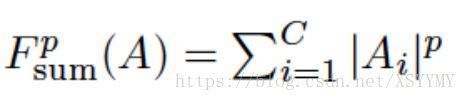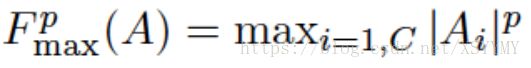深度神经网络加速和压缩

模型加速与压缩方法分类总结

• Low-Rank
• Pruning
• Quantization
• Knowledge Distillation
• Compact Network Design

 

Low-Rank

Previous low-rank based methods:

• SVD
- Zhang et al., “Accelerating Very Deep Convolutional Networks for Classification and Detection”. IEEE TPAMI 2016.

• CP decomposition
- Lebedev et al., “Speeding-up Convolutional Neural Networks Using Fine-tuned CP- Decomposition”. ICLR 2015.

• Tucker decomposition
- Kim et al., “Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications”. ICLR 2016.

• Tensor Train Decomposition
- Novikov et al., “Tensorizing Neural Networks”. NIPS 2016.

• Block Term Decomposition
- Wang et al., “Accelerating Convolutional Neural Networks for Mobile Applications”. ACMMM 2016.

 

Recent low-rank based methods:

• Tensor Ring (TR) factorizations
- Wang et al., “Wide Compression: Tensor Ring Nets”. CVPR2018

• Block Term Decomposition For RNN
- Ye et al., “Learning Compact Recurrent Neural Networks with Block-Term Tensor Decomposition ”. CVPR2018.

Why low-rank is not popular anymore?

• Low-rank approximation is not efficient for those 1x1 convolutions
• 3x3 convolutions in bottleneck structure have less computation complexity
• Depthwise convolution or grouped 1x1 convolution is already quite fast.

 

Pruning

Recent progress in pruning :

• Structured Pruning
– Yoon et al. “Combined Group and Exclusive Sparsity for Deep Neural Networks”. ICML2017
– Ren et al. “SBNet: Sparse Blocks Network for Fast Inference”. CVPR2018

• Filter Pruning
– Luo et al. “Thinet: A filter level pruning method for deep neural network compression”. ICCV2017
– Liu et al., “Learning efficient convolutional networks through network slimming”. ICCV2017
– He et al. “Channel Pruning for Accelerating Very Deep Neural Networks”. ICCV2017

• Gradient Pruning
– Sun et al. “meProp: Sparsified Back Propagation for Accelerated Deep Learning with Reduced Overfitting”. ICML2017

• Fine-grained Pruning in a Bayesian View
– Molchanov et al. “Variational Dropout Sparsifies Deep Neural Networks”. ICML2017

Structured Pruning

Previous group pruning methods mainly use the group sparsity，Yoon et al. use both group sparsity and exclusive sparsity

• Group Sparsity: Impose sparsity regularization on grouped features to prune columns of weight matrix.

• Exclusive Sparsity: promotes competition for features between different weights to learn effective filters

 

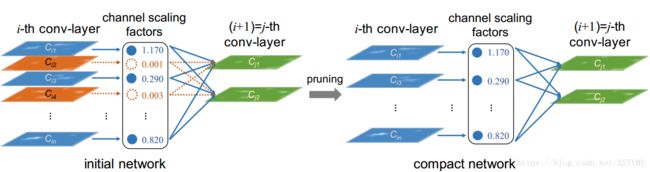
Network Slimming

• Associate a scaling factor with each channel
• Impose sparsity regularization on these scaling factors
• Prune those channels with small scaling factors

Liu et al., “Learning efficient convolutional networks through network slimming”. ICCV2017

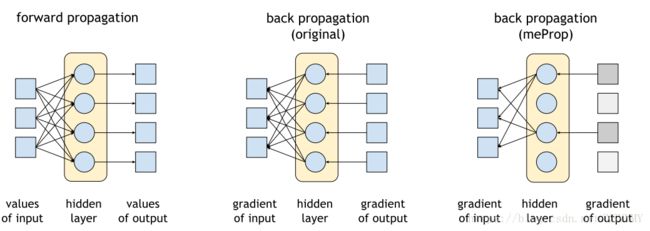
meProp

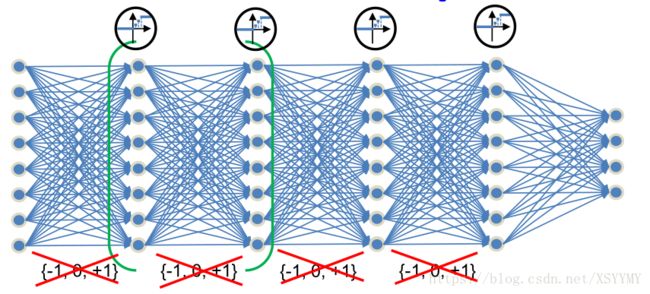
Previous pruning methods are mainly to prune weights, meProp is proposed to prune gradients to speed up training phase.

• Keep top-k gradients of neural nodes , and prune rest of them
• Since some neural nodes’ gradients are zeros, back propagation can be accelerated.

Sun et al. “meProp: Sparsified Back Propagation for Accelerated Deep Learning with Reduced Overfitting”. ICML2017

Quantization

• Low-bit Quantization
– Leng et al. “Extremely Low Bit Neural Network: Squeeze the Last Bit Out with ADMM”. AAAI2018
– Hu et al. “From Hashing to CNNs: Training Binary Weight Networks via Hashing”. AAAI2018
– Wang et al. “A General Two-Step Quantization Approach for Low-bit Neural Networks with High Accuracy”. CVPR2018

• Quantization for general training acceleration
– Köster et al. “Flexpoint: An Adaptive Numerical Format for Efficient Training of Deep Neural Networks”. NIPS2017

• Gradient Quantization for distributed training
– Alistarh et al. “QSGD: Communication-Efficient SGD via Gradient Quantization and Encoding”. NIPS2017
– Wen et al. “TernGrad: Ternary Gradients to Reduce Communication in Distributed Deep Learning”. NIPS2017

Low-bit Quantization via ADMM

Since quantization function is non-differentiable, most low-bit quantization method approximate the gradients of weights by “Straight-through” estimator. Recently Leng et al. proposed to train low-bit networks via ADMM.

They formulate neural networks with low-bit constraint on W as follows:

By introducing an auxiliary variable G

Binary Weight Network via Hashing

• Solve the binary weight via hashing
• Minimize the quantization error of inner-product similarity:

By a few transformations:

Turns out a Inner Product Preserving Hashing problem:

 

Two-Step Quantization

Stage-1

Stage-2

Wang et al.“A General Two-Step Quantization Approach for Low-bit Neural Networks with High Accuracy”.CVPR2018

• Quantize both weight and actition is diffifult
• Inspired by Two-Step Hashing, Two-Step quantization method first quantizes the activation, then quantize the weights

Flexpoint

• Previous network quantization methods mostly focus on the inference phase, Flexpoint is an effective method for training.
• Core idea is exponent sharing, data in the same tensor share the same exponent.

Köster et al. “Flexpoint: An Adaptive Numerical Format for Efficient Training of Deep Neural Networks”. NIPS2017

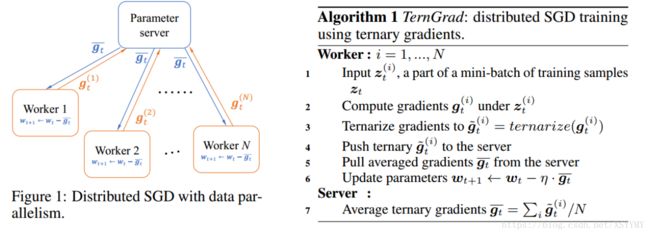
Gradient Quantization for Distributed Deep Learning

• Distributed SGD is fast, but it is limited by communication cost
• gradients communication between servers and workers is expensive.
• Reduce the communication cost by gradient quantization

Wen et al. “TernGrad: Ternary Gradients to Reduce Communication in Distributed Deep Learning”. NIPS2017

 

Knowledge Distillation

Two key steps:

• Define knowledge
• Define optimization loss which learns knowledge from teacher network

Previous Methods:

• KD (Knowledge Distillation)
- Hinton et al. “Distilling the knowledge in a neural network”. arXiv preprint arXiv:1503.02531.

• FitNets
– Romero et al. “Fitnets: Hints for thin deep nets”.ICLR 2015

Recent progress in Knowledge Distillation:

• Yim et al. “A Gift From Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning ”. CVPR2017
• Zagoruyko et al. “Pay More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer”. ICLR2017
• Chen et al. “Learning Efficient Object Detection Models with Knowledge Distillation”. NIPS2017

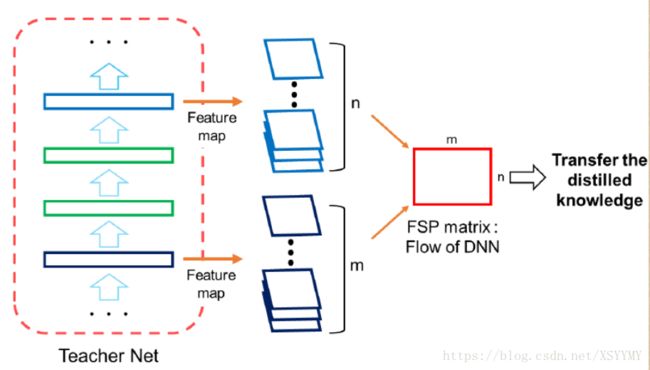
• Knowledge Definition: (FSP) flow of solution procedure matrix

• Loss Definition: L2 loss

Yim et al. “A Gift From Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning ”. CVPR2017.

 

• Knowledge Definition: activation based attention                                            

                                                                                                      

                                               

                                                                      

• Loss Definition: Normalized L2 loss

Zagoruyko et al. “Pay More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer”. ICLR2017

 

 

Compact Network Design

• Howard et al. “MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications”. CVPR2017
• Sandler et al. “Inverted Residuals and Linear Bottlenecks: Mobile Networks for Classification, Detection and Segmentation”. CVPR2018
• Zhang et al. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. CVPR2018

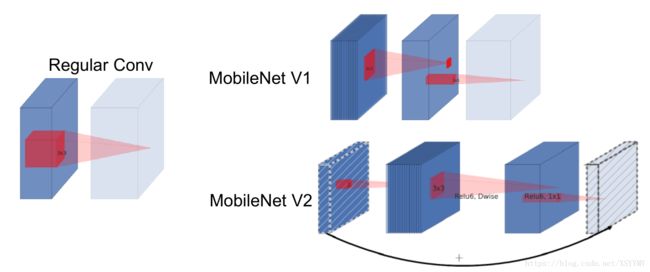
MobileNet

Howard et al. “MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications”. CVPR2017
Sandler et al. “Inverted Residuals and Linear Bottlenecks: Mobile Networks for Classification, Detection and Segmentation”. CVPR2018

 

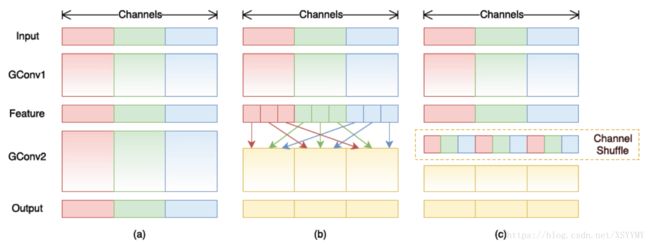
ShuffleNet

• Grouped 1x1 convolution
• Channel shuffle to enhance Information flow across channels

Zhang et al. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. CVPR2018

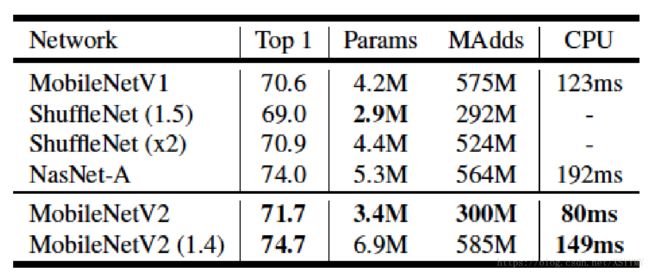
Comparison Result

Future Trends

• Non-fine-tuning or Unsupervised Compression
• Self-adaptive Compression
• Network Acceleration for other tasks
• Hardware-Software Co-design
• Binarized Neural Networks