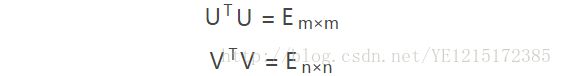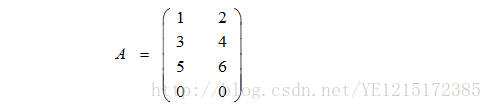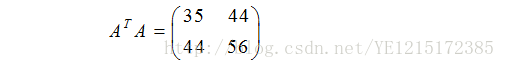奇异值分解(SVD)理论与python实现
奇异值分解(Singular Value Decomposition,SVD)是一种重要的矩阵分解(Matrix Decomposition)方法,可以看做对称方正在任意矩阵上的一种推广,该方法在机器学习的中占有重要地位。
首先讲解一下SVD的理论,然后用python实现SVD,并应用于图像压缩。
1、奇异值分解(SVD):
设有 A是一个m×n 的实矩阵,则存在一个分解使得:
U 和 V 都是正交矩阵 ,即:
Σ 是一个非负实对角矩阵,U 和 V 的列分别叫做 A 的 左奇异向量和 右奇异向量,Σ 的对角线上的值叫做 A 的奇异值。关于这三个矩阵的求解,如下:
1)、U 的列由 AAT 的特征向量构成,且特征向量为单位列向量
2)、V 的列由 ATA 的特征向量构成,且特征向量为单位列向量
3)、Σ 的对角元素来源于 AAT 或 ATA 的特征值的平方根,并且是按从大到小的顺序排列的。值越大可以理解为越重要。
举个栗子,假设:
首先计算下列矩阵
的特征值和特征向量,得到特征四个特征值为:90.7354949、0.264505087、7.62118971e-19、0。
对特征向量单位化,并按特征值从大到小对特征向量按列排放,就得到了U矩阵:
同理计算下列矩阵的特征值和特征向量,得到特征两个特征值为:0.264505087、90.7354949。
对特征向量单位化,并按特征值从大到小对特征向量按列排放,就得到了V矩阵:
而Σ为特征值的平方根构成的对角矩阵:
所以:
2、用python实现SVD,并用于图像压缩
1)首先读取一张图片(1000*685):
#!/usr/bin/python
# -*- coding:utf-8 -*-
from PIL import Image
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
if __name__ == '__main__':
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
A = Image.open('girl.jpg')
a = np.array(A) #转换成矩阵2)然后可以利用python的numpy库对彩色图像的3个通道进行SVD分解:
#由于是彩色图像,所以3通道。a的最内层数组为三个数,分别表示RGB,用来表示一个像素
u_r, sigma_r, v_r = np.linalg.svd(a[:, :, 0])
u_g, sigma_g, v_g = np.linalg.svd(a[:, :, 1])
u_b, sigma_b, v_b = np.linalg.svd(a[:, :, 2]) plt.figure(facecolor = 'w', figsize = (10, 10))
# 奇异值个数依次取:1,2,...,12。来看看一下效果
K = 12
for k in range(1, K + 1):
print k
R = restore1(u_r, sigma_r, v_r, k)
G = restore1(u_g, sigma_g, v_g, k)
B = restore1(u_b, sigma_b, v_b, k)
I = np.stack((R, G, B), axis = 2)
# 将图片重构后的显示出来
plt.subplot(3, 4, k)
plt.imshow(I)
plt.axis('off')
plt.title(u'奇异值个数:%d' % k)
plt.suptitle(u'SVD与图像分解', fontsize = 20)
plt.tight_layout(0.1, rect = (0, 0, 1, 0.92))
plt.show()def restore1(u, sigma, v, k):
m = len(u)
n = len(v)
a = np.zeros((m, n))
# 重构图像
a = np.dot(u[:, :k], np.diag(sigma[:k])).dot(v[:k, :])
# 上述语句等价于:
# for i in range(k):
# ui = u[:, i].reshape(m, 1)
# vi = v[i].reshape(1, n)
# a += sigma[i] * np.dot(ui, vi)
a[a < 0] = 0
a[a > 255] = 255
return np.rint(a).astype('uint8')最后,看一下效果:
可以看到,面上的图像随着奇异值个数的增多快速清晰起来。如果图像分解时,只保留前20个奇异值,那U和V矩阵只需要20个向量,总共只需保存:3*(20*1000 + 20 + 20*685)=3*33720个数据即可,而原图却需要保存3*(1000*685)=3*685000个数据。压缩了近20倍!