Python 机器学习_基于朴素贝叶斯分类的MNIST手写数字识别

最近在学习机器学习，总觉得只学习理论的话，对于很多问题的理解不够深入，话不多少，见下：

首先推荐李航的《统计学习方法》小蓝书，对于贝叶斯理论部分讲解的很清楚，可自行翻阅（李航书上有小栗子，可以手动算一算，对于理解很有帮助）。

接着本次MNIST实例，强推一篇很好的博客点击打开链接，在看完李航关于贝叶斯的整体理论后，再 看看这个 了解一个具体的实例中，各种下标各种概率怎么理解，包括看似很假大空的Laplace平滑（实际上没有这个平滑，贝叶斯根本无法应用）。

再了解以上理论后，可以上实战了。代码如下：

数据集用的是里面只有这个文件

##没有对label进行one-hot编码版本 读取mnist数据
import tensorflow as tf
import sklearn.preprocessing
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow.examples.tutorials.mnist.input_data
from tensorflow.contrib.learn.python.learn.datasets.mnist import read_data_sets
import pickle
import gzip
import numpy as np
import math

def normalize(data):  ##将图片像素二值化
    m,n = np.array(data).shape
    for i in range(m):
        for j in range(n):
            if data[i,j] != 0:
                data[i,j] = 1
            else:
                data[i,j] = 0
    return data
        
def get_data(datapath): ##获取MNIST数据
    mnist = gzip.open(datapath, 'rb')
    train_set, valid_set, test_set = pickle.load(mnist, encoding='bytes')
    train_data = normalize(train_set[0])
    train_label = train_set[1]
    test_data = normalize(test_set[0])#.reshape(-1, 28, 28, 1)
    test_label = test_set[1]
    return train_data,train_label,test_data,test_label

def CalProb(train_data,train_label): ##根据训练集 算条件概率P(xk|y=j) 和先验概率 P(y=j) 注意这两种概率可能会为0 后面无法计算 因此一定要进行Laplace平滑 参见李航P51
    num,dimsnum = train_data.shape
    labelnum = len(set(train_label)) ##标签总个数

    pyj = np.zeros(labelnum)
    pyjk1 = np.zeros((labelnum,dimsnum))
    for i in range(num):
        label = train_label[i]
        pyj[label] = pyj[label] + 1 ###需要laplace平滑 这里是真实个数
        for j in range(dimsnum):
            pyjk1[label][j] = pyjk1[label][j] + train_data[i][j] ##因为会出现条件概率为0的情况 log无法计算 需要laplace平滑  ##算 Pj k = 1
    print('pyj个数：',pyj)
    pyjk1 = (pyjk1.T + 1) / (pyj + 2) ##条件概率 需要Laplace平滑 分母要加上xk的种类数 这里只能取0 1像素 ##P y = j && xk = 1的概率  经验主义用频率去估计概率
    pyj = (pyj + 1) / (num + labelnum) ##P y = j 的概率 先验概率 需要 Laplace平滑 分母要加上y的标签种类数
    return  pyj, pyjk1 #pk1, #, pyjk1

def CalTestProb_xk_yj(xk,pyjxk1): ##计算条件概率 P(xk|y=j)的概率的log
    return xk * np.log(pyjxk1) + (1-xk) * np.log(1-pyj

###test  这块计算 应该可以优化 
def test(test_data,test_label,pyjk1,pyj):  ##测试
    num,dimsnum = test_data.shape
    labelnum = len(set(test_label))
    acc = 0
    for i in range(num):
        testdata = test_data[i]
        p_yj_xi = np.log(pyj) ##第i个样本属于j类的概率
        for j in range(labelnum): ##计算xi 属于 第j个类别的概率
            for k in range(dimsnum):
                xk = testdata[k] ##x^i的第j个像素 或者说是 维度
                p_yj_xi[j] = p_yj_xi[j] + CalTestProb_xk_yj(xk,pyjk1[j][k])
        ##p_yj_xi
        p_y_xi = np.argmax(p_yj_xi)
        acc = acc + (p_y_xi == test_label[i])
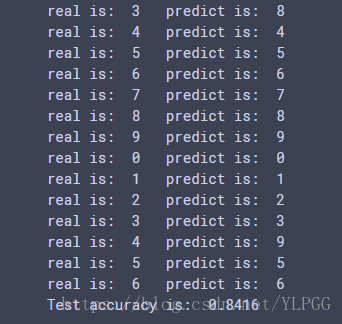
        print('real is: ',test_label[i],'  predict is: ',p_y_xi)
    print('Test accuracy is: ', acc/num)

def main():
    datapath = "C:/Users/YLP/Desktop/常用数据集/mnist.pkl.gz"
    train_data, train_label, test_data, test_label = get_data(datapath)
    pyj, pyjk1 = CalProb(train_data,train_label)
    test(test_data,test_label,pyjk1.T,pyj) 

if __name__ == "__main__":
    main()

最后我跑的结果的正确率为：84.16% 虽然远不如两层cnn或者bp的正确率，但是重在学习！

朴素贝叶斯总结：

经验主义，用频率（已有的知识）去推断概率（猜测）。

Laplace很重要，名字虽然高大上，但是代码就一句话，分子+1，分母+种类数。

一点小trick,只要计算条件概率p(xk|y=j)和p(y= j)的先验概率，不要计算p(xk)，为什么呢 因为对于一个样本来说，这个值一样啊，分母一样，只要比较分子就好了。