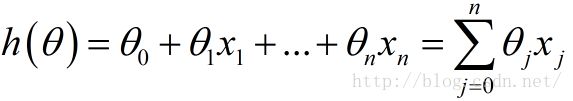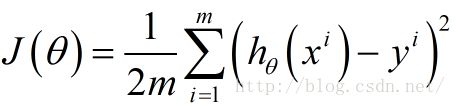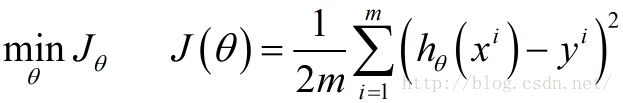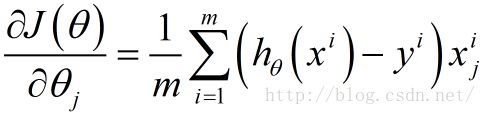梯度下降法
0. 什么是梯度
在一元函数 y = f ( x ) y=f(x) y=f(x)中,导数就是函数的变化率。
d y d x \frac{dy}{dx} dxdy
二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y),一个 z z z对应一个 x x x和一个 y y y,那就有两个导数了,一个是 z z z对 x x x的导数,一个是 z z z对 y y y的导数,称之为偏导。
[ ∂ z ∂ x ∂ z ∂ y ] \begin{bmatrix} {\frac{\partial z}{\partial x}}\\ {}\\ {\frac{\partial z}{\partial y}}\\ \end{bmatrix} ⎣⎡∂x∂z∂y∂z⎦⎤
(注意:在 x O y xOy xOy 平面内,当动点由 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)沿不同方向变化时,函数 f ( x , y ) f(x,y) f(x,y)的变化快慢一般来说是不同的,因此就需要研究 f ( x , y ) f(x,y) f(x,y) 在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)点处沿不同方向的变化率。在这里我们只学习函数 f ( x , y ) f(x,y) f(x,y)沿着平行于 x x x轴和平行于 y y y轴两个特殊方位变动时, f ( x , y ) f(x,y) f(x,y)的变化率。)
而 n n n元函数 f ( x 1 , x 2 , ⋯ , x n ) f(x_1,x_2,⋯,x_n) f(x1,x2,⋯,xn)的梯度是一个长度为 n n n的向量,向量中第 k k k个元素为函数 f f f对变量 x k x_k xk的偏导数。
[ ∂ f ∂ x 1 ∂ f ∂ x 2 … ∂ f ∂ x n ] \begin{bmatrix} {\frac{\partial f}{\partial x_1}}\\ {\frac{\partial f}{\partial x_2}}\\ {\dots}\\ {\frac{\partial f}{\partial x_n}}\\ \end{bmatrix} ⎣⎢⎢⎢⎡∂x1∂f∂x2∂f…∂xn∂f⎦⎥⎥⎥⎤
导数和偏导没有本质区别,都是当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限。
1. 什么是梯度下降法
梯度是一个向量,一个向量有大小和方向,梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!
首先,当你已经用一个训练集,暂时训练出了一个初步的模型,之所以说暂时是因为你的模型还可以继续优化,可以得到更好的效果。
把一个样本扔给模型,模型给出预测值,预测值跟我们的真实值之间存在偏差,这个偏差称为损失。每一个样本都会有损失,m个样本对应一个总的损失。
高数里我们学了多元函数,知道求一个函数的极值点,通常找到其梯度为0的点,所以我们要先求损失函数的梯度。
梯度方向是一个函数增长最快的方向,那么梯度下降就是函数减小最快的方向,损失函数的每一个值,都对应有一组 θ \theta θ ,所以在求我们最小损失函数的这个过程中,我们一直在不断地更新我们地 θ \theta θ。
2. 常见的三种梯度下降法
Batch gradient descent: Use all examples in each iteration;
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,每迭代一步,都要用到训练集所有的数据。
Stochastic gradient descent: Use 1 example in each iteration;
随机梯度下降法(Stochastic Gradient Descent,简称SGD),一轮迭代只用一条随机选取的数据,利用每个样本的损失函数对θ求偏导得到对应的梯度,来更新θ。
Mini-batch gradient descent: Use b examples in each iteration,小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)。SGD太极端,一次一条,为何不多几条?MBGD就是用一次迭代多条数据的方法
3. 梯度下降的具体步骤
首先,当你已经用一个训练集,暂时训练出了一个初步的模型,之所以说暂时是因为你的模型还可以继续优化,可以得到更好的效果。
把一个样本扔给模型,模型给出预测值,预测值跟我们的真实值之间存在偏差,这个偏差称为损失。每一个样本都会有损失,m个样本对应一个总的损失。
高数里我们学了多元函数,知道求一个函数的极值点,通常找到其梯度为0的点,所以我们要先求损失函数的梯度。
梯度方向是一个函数增长最快的方向,那么梯度下降就是函数减小最快的方向,损失函数的每一个值,都对应有一组 θ \theta θ ,所以在求我们最小损失函数的这个过程中,我们一直在不断地更新我们地 θ \theta θ。
批量梯度下降法为例:
1.目标函数
2.定义损失函数
3.目的是最小化损失函数
4.求损失函数关于 θ \theta θ 的每一个分量的偏导数
5.更新 θ \theta θ 的每一个分量 θ j \theta_j θj: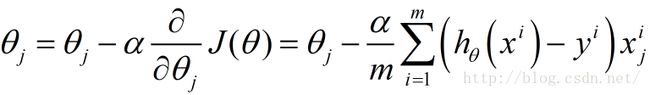
6. 好了,这就完成了一次迭代!
一次迭代的输出结果就是一个 θ \theta θ, θ \theta θ是一个向量,
[ θ 1 θ 2 … θ j … θ n ] \begin{bmatrix} {\theta_1}\\ {\theta_2}\\ {\dots}\\ {\theta_j}\\ {\dots}\\ {\theta_n}\\ \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎡θ1θ2…θj…θn⎦⎥⎥⎥⎥⎥⎥⎤