Python实现SGD、BSGD、MiniBachSGD

gradientdecnt.py

import numpy as np
import matplotlib.pyplot as plt

class LRGrad:
    def __init__(self, X, y,type='FULL',batch_size=16, alpha=0.1, shuffle=0.1, theta = None,epoch=100):
        '''
        :param X:feature vectors of input
        :param y:label of input
        :param alpha:learning rate
        :param shuffle:when |loss_new-loss|
        self.X = np.array(X)
        self.y = np.array(y).reshape(-1, 1)
        self.alpha = alpha
        self.shuffle = shuffle_
        self.col = self.X.shape[1]+1#the number of columns of data
        self.m = self.X.shape[0]#the number of rows of data
        self.X = np.hstack((np.ones((self.m, 1)), self.X))#add a column of ones to X
        self.theta = np.ones((self.col, 1))
        self.grad = np.ones((self.col, 1))
        self.epoch = epoch
        self.type = type
        self.batch_size = batch_size

    #feature normalization
    def feature_normaliza(self):
        mu = np.zeros((1, self.X.shape[1]))
        sigma = np.zeros((1, self.X.shape[1]))
        mu = np.mean(self.X, axis=0)
        sigma = np.std(self.X, axis=0)
        #X第一列都是1，不必归一化
        for i in range(1, self.X.shape[1]):
            self.X[:, i] = (self.X[:, i]-mu[i])/sigma[i]
        for j in range(1,self.X.shape[1]):
            self.X[:, i] = (self.X[:, i] - min(self.X[:, i])) / (max(self.X[:, i])-min(self.X[:, i]))
        return self.X
    #Compute grad
    def compute_grad(self):
        if self.type == 'FULL':
            h = np.dot(self.X, self.theta)
            self.grad = np.dot(np.transpose(self.X), h-self.y)/self.m
        elif self.type == 'SGD':
            r = np.random.randint(self.m)
            h = np.dot(np.array([self.X[r,:]]), self.theta)
            self.grad = np.dot(np.transpose(np.array([self.X[r,:]])), h - np.array([self.y[r,:]]))

        elif self.type == 'MINI':
            r = np.random.choice(self.m,self.batch_size,replace=False)
            h = np.dot(self.X[r,:], self.theta)
            self.grad = np.dot(np.transpose(self.X[r,:]), h - self.y[r,:]) / self.batch_size
        else:
            print("NO such gradient dencent Method!")
        return self.grad

    def update_theta(self):
        self.theta = self.theta - self.alpha*self.grad
        return self.theta

    def compute_RMSE(self):
        hh = np.dot(self.X, self.theta)
        RMSE = np.sqrt(np.dot((np.transpose(hh-self.y)),(hh-self.y))/(2*self.m))
        return RMSE
    def run(self):
        self.X = self.feature_normaliza()
        self.grad = self.compute_grad()
        loss = self.compute_RMSE()
        self.theta = self.update_theta()
        loss_new = self.compute_RMSE()
        i = 1
        print('Round {} Diff RMSE: {}'.format(i, np.abs(loss_new-loss)[0][0]))
        history = [[1], [loss_new[0][0]]]
        while np.abs(loss_new-loss)> self.shuffle:
            self.grad = self.compute_grad()
            self.theta = self.update_theta()
            if self.type == 'FULL':
                loss = loss_new
                loss_new = self.compute_RMSE()
            else:
                if i % self.epoch == 0:
                    loss = loss_new
                    loss_new = self.compute_RMSE()
            i += 1
            history[0].append(i)
            history[1].append(loss_new[0][0])
            print('Round {} Diff RMSE: {}'.format(i, np.abs(loss_new-loss)[0][0]))
        best_theta = self.theta
        return history,best_theta
    def plot_loss(self,history):
        fig = plt.figure(figsize=(8, 6))
        plt.plot(history[0], history[1])
        plt.xlabel('Number of iterations')
        plt.ylabel('RMSE')
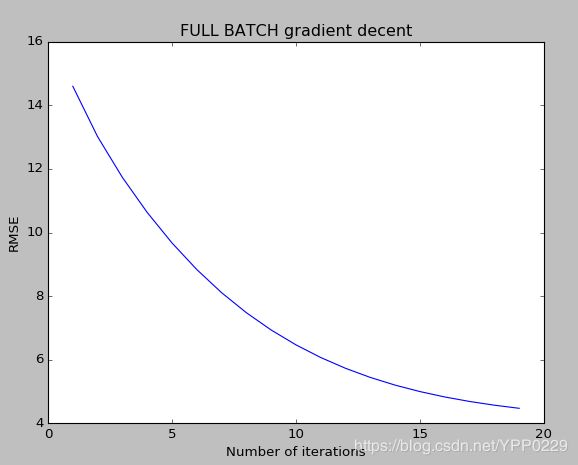
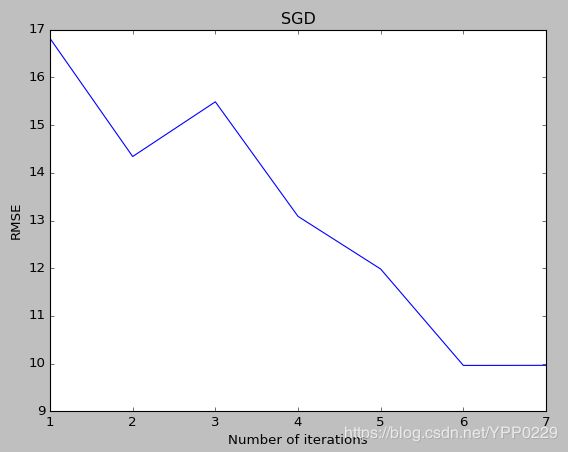
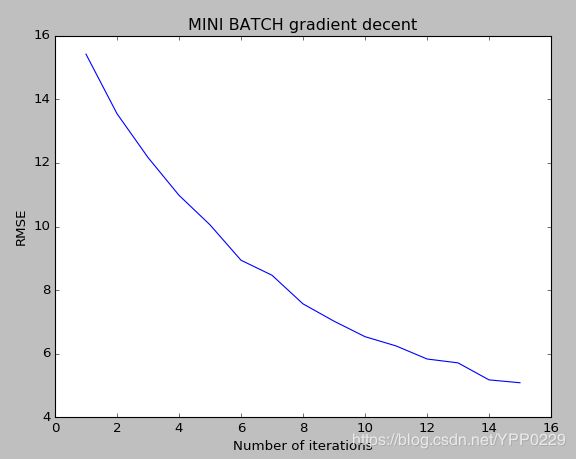
        plt.title([self.type + ' BATCH gradient decent' if self.type != 'SGD' else 'SGD'][0])
        plt.show()

上面这段代码，我们定义了一个执行梯度下降算法的类Class LRGrad，现在，我将这个类中包含的方法简单地画出来，可见在这个类中，我们总共定义了8个函数：

example.py

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from gradientdecent import LRGrad
from sklearn.datasets import load_boston
#一元线性回归
# train = pd.read_csv('../data/train.csv')
# X=train[['id']]
# y=train['questions']

#多元线性回归
# data = pd.read_csv('../data/hpdata.csv',names=['area','num_rooms','price'])
# X = data[data.columns[:-1]]
# y = data[data.columns[-1]]

#sklearn数据集
boston = load_boston()

X,y = boston.data,boston.target
print(X.shape)
lr = LRGrad(X,y,'FULL',alpha=0.1,epoch=1)
history,best_theta = lr.run()
print(best_theta)
print(history)
lr.plot_loss(history)

参数选择"Full"时

参数选择"SGD"时

参数选择"MINI"时