莫凡Python学习笔记——PyTorch动态神经网络（二）

内容原文：https://morvanzhou.github.io/tutorials/machine-learning/torch/

利用PyTorch搭建神经网络

神经网络可以使用PyTorch的torch.nn包来构建。
autograd实现了反向传播的功能，但是直接用来深度学习的代码在很多情况下还是稍显复杂。
torch.nn是专门为神经网络设计的模块化接口，nn构建于autograd之上，可以用来定义和运行神经网络。nn.Moudle是nn中最重要的类，可把它看成是一个网络的封装，包含网络各层定义以及forward方法，调用forward(input)方法，可返回前向传播的结果。

一个典型的神经网络训练过程如下：

• 定义具有一些可学习参数（或权重）的神经网络
• 迭代输入数据集
• 通过网络处理输入
• 计算损失（输出的预测值于实际值之间的距离）
• 将梯度传播回网络
• 更新网络的权重，通常使用一个简单的更新规则：weight = weight - learning_rate * gradient

1、Variable变量
在神经网络里，数据都是Variable变量的形式，是把tensor的数据放入神经网络的variable变量中，来慢慢更新神经网络中的参数。

import torch
from torch.autograd import Variable

tensor = torch.FloatTensor([[1,2],[3,4]])
variable = Variable(tensor,requires_grad=True)  #用Variable将tensor放入variable变量中

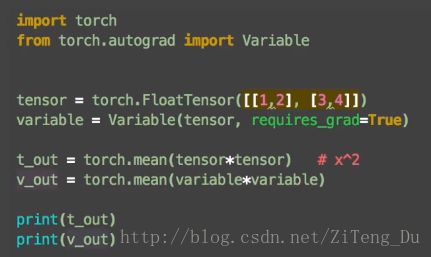
运行结果：

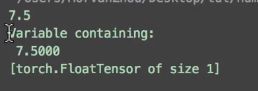
可以看到tensor的结果是7.5，variable的结果是Variable containing巴拉巴拉下面一堆，这说明。tensor只得到一个结果，而variable却是属于图的一部分，什么图呢，就是神经网络的流程图，这里有必要提到PyTorch于TensorFlow的区别了，TensorFlow是先建立一个静态的流程图在放数据，而PyTorch是一边放数据一边搭图，所以tensor不能够作为神经网络中的变量，因为它不是图的一部分同时也不能进行反向传播。
下面来看下两者在反向传播中的差别：

variable是神经网络中的变量，它有梯度grad的属性，也有data的属性，它的data的属性就是tensor类型的数据，所以从variable转化为Numpy的话，要用variable.data.numpy()，也就是先转为tensor再转为numpy。
而tensor只是数据并没有任何属性。

2、激励函数（Activation Function）
首先来看神马是激励函数：

现实生活中很多问题都是非线性的，不规则的，所以这就需要激励函数帮助我们处理这些非线性问题。
Linear function：y = wx
Unlinear function： y = AF(Wx) 其中AF就是激励函数，其实激励函数就是一个非线性函数，将这个非线性函数作用在线性结果上，强行将线性结果变非线性，从而使输出结果也会带有非线性的特征。

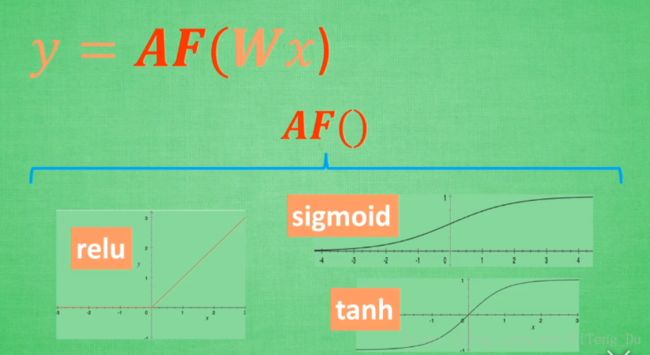
甚至可以自己创造激励函数处理问题，但是要保证你的激励函数是可以微分的，因为误差反向传播的过程，只有可以微分的函数才可以将误差反向传递回去。
当神经网络层数较少的情况下，你可以随意选择激励函数都没问题，但是当神经网络层数较多的情况下，就不能在随意选择了，因为会涉及到梯度消失，梯度爆炸的问题。
卷积神经网络中推荐用relu，循环神经网络中推荐用relu和tanh。

下面来看下激励函数的用法：

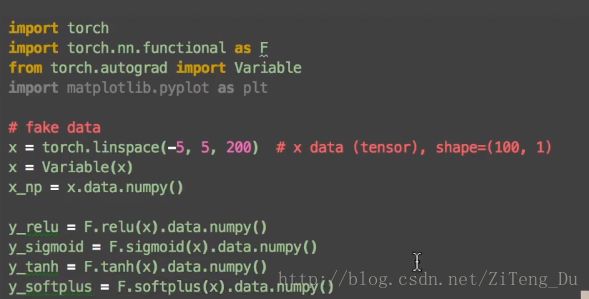
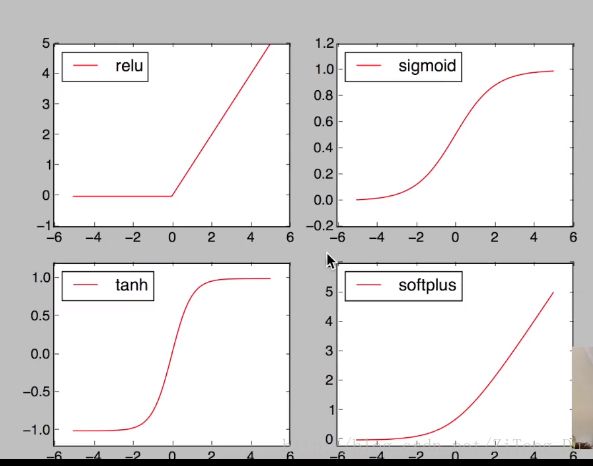
注意在神经网络中进行运算的数据都是variable变量，所以要接受激励函数的作用就要先将numpy的数据利用torch.tensor(numpy)来转化为variable类型的数据，但是使用matplotlib画图的时候还是需要numpy的数据，所以要利用x.data.numpy()来转化回numpy。

3、初步搭建神经网络

（1）关系拟合回归:

import torch
from torch.autograd import Variable
import torch.nn.function as F
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1,1,100),dim=1) #因为在torch中它的数据是有维度的，unsqueeze就是把一维的数据转化为二维
y = x.pow(2) + 0.2*torch.rand(x.size())
x,y = Variable(x), Varitable(y)
#plt.scatter(x.data.numpy(),y.data.numpy())  #这里是画图
#plt.show()

#下面开始搭建神经网络：
class Net(torch.nn.Module):
    #init中设置好每一层的输入输出口有几个
	def __init__(self,n_feature,n_hidden,n_output):
		super(Net,self).__init__()
		self.hidden = torch.nn.Linear(n_features,n_hidden)
		self.predict = torch.nn.Linear(n_hidden,n_output)
	#forward才算是真正开始搭建神经网络,x是输入信息，
	def forward(self,x):
		#输入数据先经过一个隐藏层，然后再用激励函数激活
		x = F.relu(self.hidden(x))
		#再让x经过输出层，这里可以不再用激励函数激活，因为大多数我们所预测的结果的取值都是从正无穷到负无穷，所以并不需要使用激励函数进行截取（因为一般的激励函数的值域都只是在一定区间内）
		x = self.predict(x)
		return x
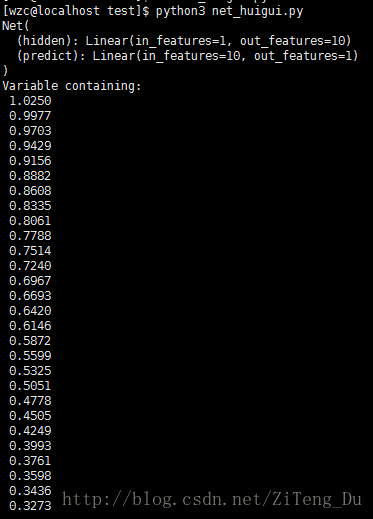
net = Net(1,10,1)
print(net)
#到此为止，神经网络就算是搭建完成了

总结下以上的一些类：

• torch.Tensor是一个多维数组，于ndarrary类似，只不过可以利用张量在GPU上加速运算
• Variable:是神经网络内的变量，variable不仅含有数据，也包括数据在神经网络中的一些操作行为，换句话说variable就是用来包装tensor，并且记录tensor数据在网络中的历史操作，variable有梯度grad。
• nn.Module 是一个神经网络模块，说白了就是一个封装好的网络，包含初始化，网络中每层的定义等，我们可以通过继承这个类，重写它的函数来方便的形成我们自己的网络。
• torch.functional是torch的方法类，用来获得激励函数。

计算损失函数并更新权重：

我们使用神经网络的优化器来对网络参数进行优化，，torch.optim中有很多optimizer，这里使用的是SGD，net.parameters()就是网络中所有的参数，lr是学习率，学习率越高，学习的越快，但是学习的越快就会忽视一些内容，造成学习效率并不高的结果，所以一般lr小于1。

损失函数采用（output，target）输入对，并计算预测输出结果与实际目标的距离。
在nn包里有几种不同的损失函数，一个简单的损失函数是nn.MSELoss计算输出和目标之间的均方误差，回归问题用这个就足够了，如果是分类问题，就用另外一个，下面会提到

optimizer = torch.optim.SGD(net.parameters(),lr=0.5)#定义优化器
loss_func = torch.nn.MSELoss()  #计算损失值

#开始训练
for t in range(100):
	prediction = net(x) #经过网络得到结果
	loss = loss_func(prediction,y)    #计算预测值与真实值之间的距离，注意顺序，loss_func(预测值，真实值)，因为反过来有可能会出错。
	optimizer.zero_grad()    #把之前的梯度清零，否则梯度会累加之前的梯度（详细的原因还在探究中，稍后补上）
	loss.backward() #进行反向误差传播，计算各结点梯度
	optimizer.step()  #用optimizer优化更新网络参数

（2）分类神经网络

整体的代码和回归其实都差不多，只需修改下数据和损失函数。

import torch
from torch.autograd import Variable
import torch.nn.functional as F
import matplotlib.pyplot as plt

n_data = torch.ones(100,2)
x0 = torch.normal (2*n_data,1)
y0 = torch.zeros(100)
x1 = torch.normal(-2*n_data,1)
y1 = torch.ones(100)
x = torch.cat((x0.x1),0).type(torch.FloatTensor)
y = torch.cat((y0,y1),).type(torch.LongTensor)

x,y = Variable(x), Variable(y)

class Net(torch.nn.Module):
      def __init__(self,n_feature,n_hidden,n_output):
            super(Net,self).__init__()
            self.hidden = torch.nn.Linear(n_feature,n_hidden)
            self.predict = torch.nn.Linear(n_hidden,n_output)
      def forward(self,x):
            x = F.relu(self.hidden(x))
            x = self.predict(x)
            return x
 net = Net(2,10,2)
 print(net)

optimizer = torch.optim.SGD(net.parameters(),lr=0.02)
loss_func = torch.nn.CrossEntropyLoss()

for t in range(100):
     prediction = net(x)
     loss = loss_func(prediction,y)
     optimizer.zero_grad()
     loss.backward()
     optimizer.step()