状态压缩.宝藏(noip2017day2t2)正解
题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 n 个深埋在地下的宝藏屋, 也给出了这 n 个宝藏屋之间可供开发的 m 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。
新开发一条道路的代价是:
L×K
L代表这条道路的长度,K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代 价最小,并输出这个最小值。
输入输出格式
输入格式:
第一行两个用空格分离的正整数 n 和 m,代表宝藏屋的个数和道路数。
接下来 m 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏 屋的编号(编号为 1~n),和这条道路的长度 v。
输出格式:
输出共一行,一个正整数,表示最小的总代价。
输入输出样例
输入样例#1:
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
输出样例#1:
4
输入样例#2:
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 2
输出样例#2:
5
说明
【数据规模与约定】
对于 20%的数据: 保证输入是一棵树,1≤n≤81≤n≤8,v≤5000v≤5000 且所有的 v 都相等。
对于 40%的数据: 1≤n≤81≤n≤8,0≤m≤10000≤m≤1000,v≤5000v≤5000 且所有的 v 都相等。
对于 70%的数据: 1≤n≤81≤n≤8,0≤m≤10000≤m≤1000,v≤5000v≤5000
对于 100%的数据: 1≤n≤121≤n≤12,0≤m≤10000≤m≤1000,v≤500000
这道题今年也坑害( 也成就 )了一大堆人。
相信大部分人看到这道题的数据,想的就是状压。但是具体怎么处理呢?
考完之后很多人都听到了什么记忆化搜索,贪心什么的。比如说我就在网上看到过这么一个题解:
用邻接矩阵存边,f[i] 和dis[i]表示已选点状态为i,每个点距离为dis[i]时的最优答案,每次回溯dis[i],枚举一遍根节点,取个min作为答案,这样每个状态最多更新n^2次(大概吧) 总复杂度是n^3*2^n。
事实上这也是很多人的想法,在网上搜到的很多题解也都是类似这样的做法。因为这种做法的状态很好想,只要一维状态表示选取的点就够,然后按照上面的题解做就行了。但是我们考虑时间复杂度。
首先这种做法肯定不能采用循环赋值,如果用dfs不进行剪枝阶乘级别的时间复杂度也坑定T飞。
这个题解(也是大部分人)的做法是记忆化,也就是每个状态只搜索一次。可这显然也是错误的。因为只枚举点的状态,这道题你选取的边也会对后面有影响,也就是我们dp入门时一直强调的所谓后效性的有无。
然后我又在网上看到这样一篇题解。状态相同,dfs的时候加了限制条件:如果能更新就继续dfs下去,如果不能就不dfs。这种做法看上去好像是对的,也能在今年的noip上AC。
然而这实际上是因为今年noip数据水,导致记忆化搜索,贪心,和这个dp都能AC!
我们思考这个为什么错。也同样是因为后效性!这种状态下现在的最优并不代表之后仍然是最优。也许这样说有点抽象,我们拿具体的例子来说: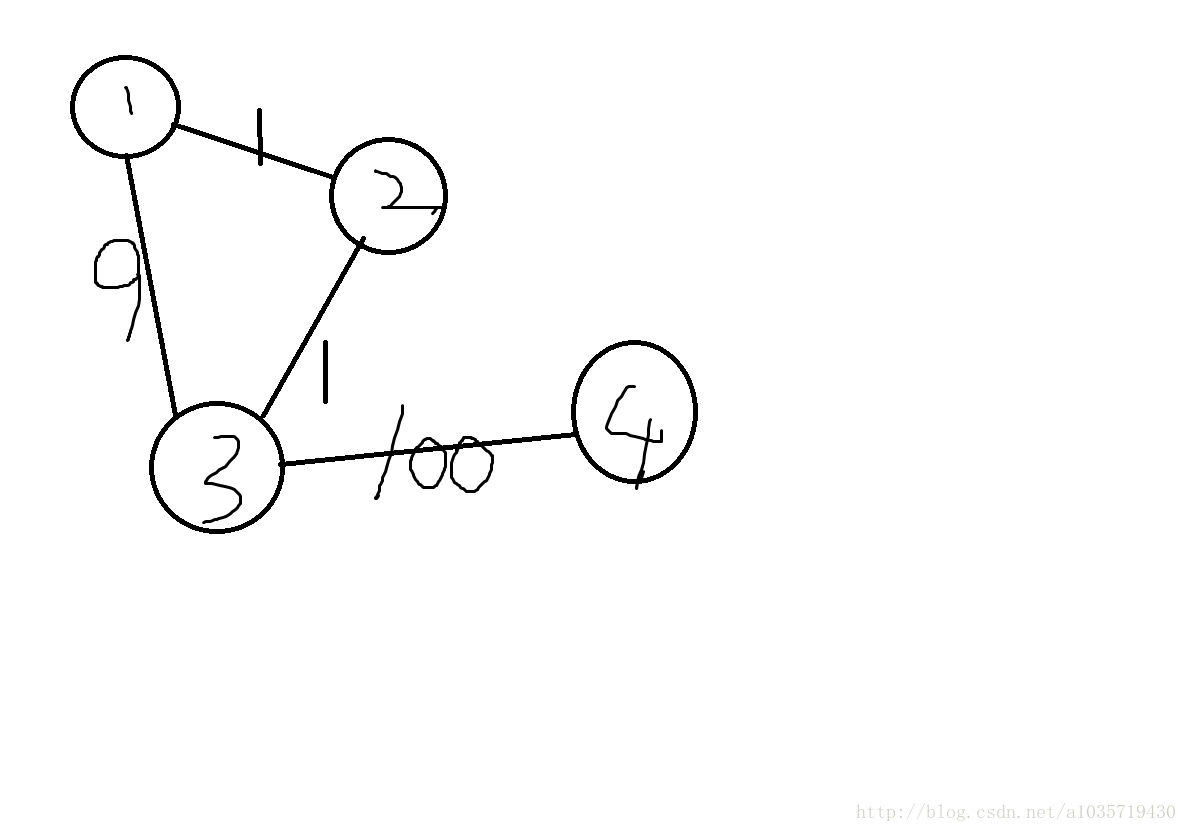
考虑从1节点开始搜,如果按照更新的原则,如果按照1—>2—>3先搜的话,再搜1—3的时候就不会更新了,显然易见可以发现后者比前者更优。这也就是后效性的影响。
这道题的正确做法是状压无疑(不考虑一些骚算法如什么模拟退火= =)
那么我们为了使dp无后效性可以加一维甚至多维来限制,达到无后效性的效果。然后就可以循环复制或者记忆话的dfs了。
考虑这道题的特性,如果确定根节点,我们挖出来的必然是一棵树。
那么我们可以利用树深度的特性来处理。
我采用的是f【i】【j】【s】表示 j 距离根节点为 i ,我们要从 j 开始往下挖出 s 的集合。那么如果i,j,s确定了 他的值是确定的,不会受到前面的选择的影响。
同时 i , j<=12,s<=2^12,每个状态都会被搜到一次 最坏情况下也不会TLE !
好,那我们考虑状态转移。
对于一个状态,经过思考我们发现,我们可以枚举这个状态中s中的一个点,继续拓展。那么我们可以得到状态转移方程:
f[i][j][s](j∉s)=mins2∈s,k∈s(d[j][k]∗(i+1)+f[i][j][s−s2]+f[i+1][j][s2−k]) f [ i ] [ j ] [ s ] ( j ∉ s ) = m i n s 2 ∈ s , k ∈ s ( d [ j ] [ k ] ∗ ( i + 1 ) + f [ i ] [ j ] [ s − s 2 ] + f [ i + 1 ] [ j ] [ s 2 − k ] )
大家要好好揣摩这个状态转移方程的意思。(这是很关键的一个点)
那么我们只要赋好初值(状态为0的情况),然后枚举根节点。dfs取f[0][i][s-i]的最小值即可。
这道题的难点就在于这个状态转移方程难以想,还是要利用好图形的特性。
dfs代码如下:
void dfs(int deep,int j,int zh)
{
check[deep][j][zh]=true;
for(int k=1;k<=n;++k)
if((zh&(1<1))!=0&&f[j][k]!=168430090)
for(int zh2=zh;zh2 >= 1;zh2=(zh2-1)&zh)
{
if((zh2&(1<1))==0) continue;
if(!check[deep+1][k][zh2-(1<1)]) dfs(deep+1,k,zh2-(1<1));
if(!check[deep][j][zh-zh2]) dfs(deep,j,zh-zh2);
dp[deep][j][zh]=min(dp[deep][j][zh],f[j][k]*(deep+1)+dp[deep+1][k][zh2-(1<1)]+dp[deep][j][zh-zh2]);
}
return;
} 但我们再回过头来看这个过程,是不是太暴力,太复杂了。
作为一道NOIP的T2,这么大的难度显然是不太合适的。
肯定是我们的思路不够优秀
我们考虑状态设计。
其实我们发现我们这里有很多多余的转移,而且在转移的过程中也不是非常的优秀,没有一定的状态关系。
更好的做法见:
https://blog.csdn.net/a1035719430/article/details/80488083