后缀数组(非常清楚)
后缀数组
顾名思义,后缀数组就是记录所有后缀的数组,同时,它也是有序的。后缀数组 SA 可以帮助我们解决单字符串问题、两个字符串的问题和多个字符串的问题等
比如说字符串 banana¥我们暂且把¥ 认为是一个字符(表示字符串结尾)。
我们记suffix(i)表示从原字符串第i个字符开始到字符串结尾的后缀。我们把它所有的后缀拿出来按字典序排序:

把排好序的数组记作sa
那么此时sa数组就是:7 6 4 2 1 5 3
同时rank数组表示后缀 i i 表示i在sa中的排名。
也就是说如果 sa[i]=j s a [ i ] = j 那么 rank[j]=i r a n k [ j ] = i
我们现在令 height[i] 是 suffix(sa[i-1]) 和 suffix(sa[i]) 的最长公共前缀长度,即排名相邻的两个后缀的最长公共前缀长度。
比如height[4]就是anana 和ana 和 a n a 的最长公共前缀,也就是ana,长度为3。
这个height数组有一个神奇的性质:若 rank[j]<rank[k] r a n k [ j ] < r a n k [ k ] ,则后缀 Sj..n S j . . n 和 Sk..n S k . . n 的最长公共前缀为 min(height[rank[j]+1],height[rank[j]+2]...height[rank[k]]) m i n ( h e i g h t [ r a n k [ j ] + 1 ] , h e i g h t [ r a n k [ j ] + 2 ] . . . h e i g h t [ r a n k [ k ] ] ) 。这个性质是显然的,因为我们已经后缀按字典序排列。
同时,我们还有一个结论: height[rank[i]]≥height[rank[i−1]]−1 h e i g h t [ r a n k [ i ] ] ≥ h e i g h t [ r a n k [ i − 1 ] ] − 1
证明:
设 suffix(k) s u f f i x ( k ) 是排在 suffix(i−1) s u f f i x ( i − 1 ) 前一名的后缀,则它们的最长公共前缀是 height[rank[i−1]] h e i g h t [ r a n k [ i − 1 ] ]
那么 suffix(k+1) s u f f i x ( k + 1 ) 将排在 suffix(i) s u f f i x ( i ) 的前面
并且 suffix(k+1) s u f f i x ( k + 1 ) 和 suffix(i) s u f f i x ( i ) 的最长公共前缀是 height[rank[i−1]]−1 h e i g h t [ r a n k [ i − 1 ] ] − 1
所以 suffix(i) s u f f i x ( i ) 和在它前一名的后缀的最长公共前缀至少是 height[rank[i−1]]−1 h e i g h t [ r a n k [ i − 1 ] ] − 1
证毕。
这样我们按照 height[rank[1]],height[rank[2]]...height[rank[n]] h e i g h t [ r a n k [ 1 ] ] , h e i g h t [ r a n k [ 2 ] ] . . . h e i g h t [ r a n k [ n ] ] 的顺序计算,利用 height h e i g h t 数组的性质,就可以将时间复杂度可以降为 O(n) O ( n ) 。这是因为 height h e i g h t 数组的值最多不超过n,每次计算结束我们只会减1,所以总的运算不会超过2n次。
这里我们注意到 ,所有后缀子串的前缀子串即为原串的所有子串。
那么我们就可以利用 height h e i g h t 数组解决很多问题了。
现在我们再来考虑后缀数组( rank 与 sa )怎么求
对长度为 20 2 0 的字符串,也就是所有单字母排序。
用长度为 20 2 0 的字符串,对长度为 21 2 1 的字符串进行双关键字排序。考虑到时间效率,我们一般用基数排序。
用长度为 2k−1 2 k − 1 的字符串,对长度为 2k 2 k 的字符串进行双关键字排序。
直到 2k≥n 2 k ≥ n ,或者名次数组 Rank 已经从 1 排到 n,得到最终的后缀数组。
我们来举个求后缀数组的栗子来理解一下这个过程。
对于字符串S = “aabaaaab” 过程如图:

可能这个一下子就看懂了。但是程序怎么实现呢?这是个大问题。
先上代码:
#include接下来我一步步解释这个代码。
main函数就不用解释了吧。
直接看doubling函数。
for(int i = n;i;--i)
s[i] = s[i - 1];初始化。将字符串从0~n-1移到1~n (便于操作)
for(int i = 1;i <= n;++i){
rank[i] = s[i];
sa[i] = i;
}初始化rank数组与sa数组。
对于rank数组我们如图是依次比较前 20,21,22 2 0 , 2 1 , 2 2 位的,那么初始化就是第一位的大小顺序,一开始就是原字符。sa数组排名初始就是在原数组的位置
for(int l = 0 , pos = 0 , sig = 255;pos < n;sig = pos)l是上一次排序的长度,pos是函数中用到的一个类似于标记数组下标的东西,sig是sigma的缩写,代表字符集大小,也就是上一层有多少个名次不同的后缀
for(int i = n - l + 1;i <= n;++i)
p[++pos] = i;
for(int i = 1;i <= n;++i)
if(sa[i] > l) p[ ++pos ] = sa[i] - l;p数组是根据第二关键字排的序,p[i]代表第二关键字排第i的后缀标号
也就是说 对于每一个后缀已经更具前 l=2k l = 2 k 个字符排好序了,现在需要扩展到 2k+1 2 k + 1 ,我们需要按照第 2k+1—2k+1 2 k + 1 — 2 k + 1 的字符排序,然后在根据之前拍好的序进行合并。那么后面这 2k 2 k 就是我们所谓的第二关键字。
我们显而易见的可以发现,对于后面 n−l n − l 个后缀,他都空了,显然优先级是最高的,也就是最小的,我们先把他们提出来。
然后剩余的,我们根据上一次排序的结果做。这一部分相当于是我们把前一次排序的结果直接移到我们这里第二关键字的排序,再加上每一个前缀前面 2k 2 k 的部分。(这一部分可能比较抽象,大家手糊一下就能很清楚的理解我的意思了)
那么我们就成功的求出了p数组。
memset( cnt , 0 ,sizeof(int) * (sig + 1));
for(int i = 1;i <= n;++i)
++cnt[rank[i]];
for(int i = 1;i <= sig;++i)
cnt[i] += cnt[i - 1];对于这规模为 2k 2 k 的子串,肯定有一模一样的,我们根据上一次排序得到的rank,统计相同的后缀,cnt数组的大小就是前一次,也就是第一关键字的前缀个数。
转化为前缀和方便我们后面的运算。
for(int i = n;i;--i)
sa[cnt[rank[p[i]]] -- ] = p[i];这一句比较关键,是更新我们的排名。
因为每个cnt存的是相同的前缀,也就是在第一关键字中的优先级,那么第一关键字相同的肯定排一起,所以每排一个,我们都将对应的cnt数组-1,相当于指针指向了前一位。然后其他就好懂了,我们根据排名,从后往前,在每一段里加入。
举个栗子。
原字符串:12323231
现在第一关键字是前两位,第二关键字是第3、4位。
那么当前的第一关键字
(rank数组):2 3 5 3 5 3 4 1(rank[i]表示后缀i的排名(当前情况下))
很显然:
1−>1¥ 1 − > 1 ¥ (¥暂且表示为空)
2−>12 2 − > 12
3−>23 3 − > 23
4−>31 4 − > 31
5−>32 5 − > 32
此时的第二关键字
(p数组):7 8 6 2 4 5 1 3
也很显然:
7、8−>¥¥ 7 、 8 − > ¥ ¥
6−>1¥ 6 − > 1 ¥
2、4−>23 2 、 4 − > 23
5−>31 5 − > 31
1、3−>32 1 、 3 − > 32
cnt数组:(对应rank数组)
1 1 3 1 2
第一个1:第8个后缀第一关键字最小。
第二个1:第1个后缀第一关键字次小。
第一个3:第2、4、6个后缀第一关键字次次小。(词穷0.0)
第三个1:第7个后缀次次次小。
第一个2:第3、5个后缀最大=次次次次小。
那么我们画个图来表示一下第一关键字的排名情况:
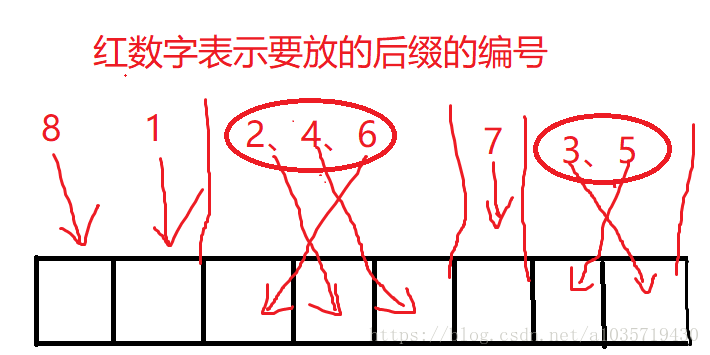
很显然,经过这次变化
新的sa数组变为:8、1、6、2、4、7、5、3
for(int i = 1;i <= n;++i)
tmp[sa[i]] = equ(sa[i] , sa[i - 1] , l)?pos:++pos;
for(int i = 1;i <= n;++i)
rank[i] = tmp[i];这里的tmp数组就相当于临时的rank数组,每次进行更新,
equ函数就是判断两个合并后的前缀是否完全相同。相同在rank里排名就相同。
那么后缀数组就愉快的讲完了。
求出了后缀数组,height数组也很好求。根据前面的性质,我们只要用一个单调队列维护即可。