机器学习知识点总结
1. LR原理
LR模型是通过把特征进行线性组合,再把组合通过一层sigmoid函数映射成结果为1或0的概率
设一个样本属于正样本的概率为p,则
P ( Y = 1 ∣ x ) = e w ⋅ x 1 + e w ⋅ x P(Y=1|x)=\frac{e^{w\cdot x}}{1+e^{w\cdot x}} P(Y=1∣x)=1+ew⋅xew⋅x
P ( Y = 0 ∣ x ) = 1 1 + e w ⋅ x P(Y=0|x)=\frac{1}{1+e^{w\cdot x}} P(Y=0∣x)=1+ew⋅x1
事件的对数几率为
l o g i t ( p ) = l o g p 1 − p = w ⋅ x logit(p)=log\frac{p}{1-p}=w\cdot x logit(p)=log1−pp=w⋅x
学习的目标是最大化似然函数,假设样本独立,则似然函数可以定义为所有样本生成概率的乘积
L ( θ ) = ∏ i = 1 n ( p i ( θ ) ) y i ∗ ( 1 − p i ( θ ) ) 1 − y i L(\theta) = \prod_{i=1}^{n}(p_i(\theta))^{y_i}*(1-p_i(\theta))^{1-y_i} L(θ)=i=1∏n(pi(θ))yi∗(1−pi(θ))1−yi
其中 p i ( θ ) p_i(\theta) pi(θ)是待求参数,由于 y i y_i yi取值为0或1,因此上式中对于每一个i,实际上只有一项。
对其取对数得
l o g ( L ( θ ) ) = y i l o g ( p i ( θ ) ) + ( 1 − y i ) l o g ( 1 − p i ( θ ) ) log(L(\theta))=y_ilog(p_i(\theta))+(1-y_i)log(1-p_i(\theta)) log(L(θ))=yilog(pi(θ))+(1−yi)log(1−pi(θ))
最小化 − l o g ( L ( θ ) ) -log(L(\theta)) −log(L(θ)),即可求得 θ \theta θ最小值
2. LR中的特征离散化
LR中经常要对连续的特征离散化,离散化的目的是增强模型的健壮性,使其对异常数据不敏感,比如对于年龄数据,可以每隔10岁作一个区间,这样对于异常数据(比如300岁,可以设置大于80岁的数据设置为0),就不太敏感,否则这些异常数据可能会对模型造成影响。
特征离散化后可以简化模型,对于年龄,如果不离散化,模型可能要对每一个岁数都要拟合,离散化后模型只需要对数个年龄段拟合。这样可以防止过拟合。
3 决策树的几个基本算法,ID3,C4.5,CART
信息熵定义为 H ( p ) = − ∑ i = 1 n p i l o g p i H(p)=-\sum_{i=1}^{n}p_ilogp_i H(p)=−i=1∑npilogpi
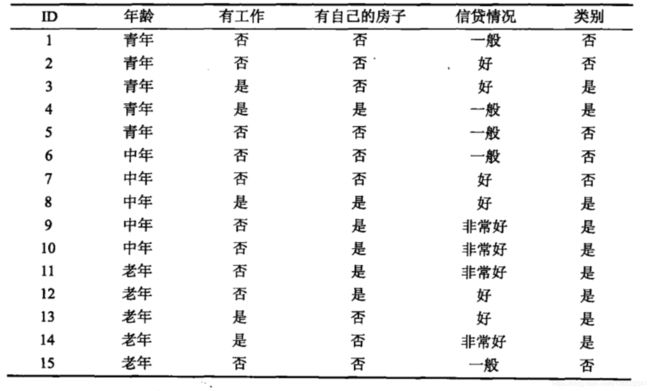
根据上图,一共有15个样本,类别为是的有9个,类别为否有6个,可以求得类别的熵为
− ( 0.6 ∗ l o g 0.6 + 0.4 ∗ l o g 0.4 ) = 0.971 -(0.6*log0.6+0.4*log0.4)=0.971 −(0.6∗log0.6+0.4∗log0.4)=0.971
另外还可以定义条件熵
H ( Y ∣ X ) = − ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X) = -\sum_{i=1}^{n}p_iH(Y|X=x_i) H(Y∣X)=−i=1∑npiH(Y∣X=xi)
比如说需要计算在有无房子这个特征下,类别的条件熵,则先计算有无房子下类别的熵,再按照房子的概率相加,有无房子的概率分布为0.4,0.6。熵计算如下:
有房子情况下的熵:
H 1 = 1 ∗ l o g 1 + 0 ∗ l o g 0 = 0 H_1 = 1*log1+0*log0 = 0 H1=1∗log1+0∗log0=0
无房条件情况下的熵:
H 2 = − ( 3 9 l o g 3 9 + 6 9 l o g 6 9 ) H_2 = -(\frac{3}{9}log\frac{3}{9}+\frac{6}{9}log\frac{6}{9}) H2=−(93log93+96log96)
因此在房子条件下,类别的熵为
H ( Y ∣ X ) = 0.4 ∗ H 1 + 0.6 ∗ H 2 H(Y|X)=0.4*H_1+0.6*H_2 H(Y∣X)=0.4∗H1+0.6∗H2
而信息增益定义为
g = H ( Y ) − H ( Y ∣ X ) = 0.42 g=H(Y)-H(Y|X)=0.42 g=H(Y)−H(Y∣X)=0.42
ID3算法核心就是计算每一个特征的信息增益,选取信息增益最大的作为结点的特征,递归构建决策树,直到信息增益很少或者已经没有需要分类的样本为止,此法只有树的生成,因此容易过拟合。
由于在用ID3算法计算信息增益时,会偏向使用取值较多的特征,这个缺陷容易带来过拟合,因此在C4.5算法中采用信息增益比来作为挑选准则,其中信息增益比定义为
g R ( D , A ) = g ( D , A ) / H A ( D ) g_R(D,A)=g(D,A)/H_A(D) gR(D,A)=g(D,A)/HA(D)
其中g(D,A)为数据集D关于特征A信息增益,而 H A ( D ) H_A(D) HA(D)是数据集D关于特征A的熵。从公式可知,如果特征A取值很多的话,其熵会很大,因此信息增益比就会减低,一定条件上改善ID3算法的缺点。
CART(Classification and Regression Tree) 与前面两种决策树算法相比,首先它是二叉树,其次这个算法能够用于生成回归树或分类树,在树生成之后,还会通过剪枝降低树的复杂度。
对于回归树,一般用平方误差 ∑ i = 1 n ( y i − f ( x i ) ) 2 \sum_{i=1}^{n}(y_i-f(x_i))^2 ∑i=1n(yi−f(xi))2作为损失函数。其中 y i y_i yi是样本的标签值, f ( x i ) f(x_i) f(xi)是分类器预测值。
当分类器构建完成时对于每个叶节点,可能会有多个标签值不同的样本。容易得知,该叶节点的预测值为这些样本值的均值。
剩下的问题是如何划分数据,这里是采用贪心算法。
对于节点中的所有样本,扫描所有特征上的每一个值,对于每一个特征X和取值S将样本划分成 X ≤ S X\le S X≤S 和 X > S X>S X>S两类,并且记录其平方损失函数。扫描完成后,找到损失函数最小的切分特征和取值,将样本划分为两类。递归进行此过程,直到满足停止条件。
对于分类树,其分类过程与ID3和C4.5算法类似。只是这里用另一个指标:基尼系数,其定义为
G i n i ( p ) = ∑ i = 1 n p k ( 1 − p k ) = 1 − ∑ i = 1 n p k 2 Gini(p)=\sum_{i=1}^{n}p_k(1-p_k)=1-\sum_{i=1}^{n}p_k^2 Gini(p)=i=1∑npk(1−pk)=1−i=1∑npk2
因为算法构建的是二叉树,所以一般在划分数据集时,是根据样本集合D中的某一特征A是否取某一可能值a分为D1、D2=D-D1两部分,在特征A的条件下,基尼系数定义为
G ( D , A ) = ∣ D 1 ∣ ∣ D ∣ G ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ G ( D 2 ) G(D,A)=\frac{|D_1|}{|D|}G(D1)+\frac{|D_2|}{|D|}G(D2) G(D,A)=∣D∣∣D1∣G(D1)+∣D∣∣D2∣G(D2)
其中 ∣ D ∣ |D| ∣D∣为样本数量。
因此CART分类树算法可以描述为:对于样本中的每一个特征,对其中的每一个取值,分别计算对应的基尼系数,选取系数最小的特征和取值作为切分点,将样本分成两部分,再递归调用算法,直到满足停止条件。
树生成之后还需要对其进行剪枝,剪枝的时候通过以下式子计算损失函数
C α ( T ) = C ( T ) + α ∣ T ∣ C_{\alpha}(T)=C(T)+\alpha|T| Cα(T)=C(T)+α∣T∣
其中C(T)为树对训练数据的预测误差,|T|是树的节点个数, α ≥ 0 \alpha\ge0 α≥0为参数,用于权衡C(T)和|T|。当 α \alpha α越大,表明需要树的节点更少才能降低损失函数,也就是模型要越简单。剪枝的过程在这里不赘述。
4. RF,XGBoost 和GBDT
这3个都属于集成学习,通过结合多个基分类器的结果来得到一个强分类器。集成学习分两类,一类是基分类器之间存在相关性,必须一个个生成,称为boosting,一类是基分类器没有相关性,可以同时生成,称为bagging。其中Random Forest是bagging,而GBDT和XGBoost为boosting。
随机森林是构建多个决策树,再利用这些决策树进行投票来对样本进行分类或回归。构建的过程包括:随机选择样本,随机选择特征,构建树,投票。
随机森林优点很多,其性能很好,能够自动处理高维数据,不用自己选择,并且能够给出每个特征的重要性。缺点是在噪声大的问题上容易过拟合。
GBDT是新型的Boosting方法,通过拟合损失函数在前面N个树模型预测值的负梯度值,从而通过梯度下降法来降低损失函数。好处是能够处理各种数据,准确度高。缺点是不能并行训练数据。而XGBoost是能够并行生成树的,加快了模型的生成速度。
XGBoost相比与GBDT作了很多优化,包括:
- GBDT一般以CART树作为基学习器,而XGBoost除此之外还支持用线性分类器等多种分类器
- GBDT在拟合时用了损失函数的一阶导数,而XGBoost用了二阶泰勒展开。
- XGBoost在损失函数中加入了正则项,抑制模型复杂度,防止过拟合
- 缩减(shrinkage),此项不明白。
- 列抽样,每次生成新分类器都随机抽取特征,防止过拟合和减少计算
- 对缺失值有特定的处理
- 支持并行。虽然Boosting需要按顺序生成每一棵树,但是在生成1颗树的时候,需要计算特征的增益,此时可以利用并行化。
- GBDT利用梯度下降对损失函数进行优化,XGBoost用牛顿法来优化
LR与XGBoost和GBDT的一些区别:
LR擅长处理离散数据,而且对高维稀疏特征处理比GBDT要好。
因为GBDT和LR的正则方式不一样,LR是靠抑制权重值的大小防止过拟合,GBDT是靠抑制树的大小来防止过拟合,在高维稀疏特征中,可能只要很少叶节点就能完美区分样本,因此GBDT的方式失效。而LR的正则化能够防止某一个节点的权重值过大,因此其能够防止高维稀疏特征的过拟合
通常条件下GBDT比LR和SVM表现要好,原因为:
- GBDT集成了多个基分类器,所以泛化能力高
- SVM需要自行选择核函数等超参数,而GBDT的超参数学习能力都不错,因此泛化能力比SVM和LR要好
4.1 XGBoost如何做分类和回归
在分类时,本质也是用的回归树,因为如果用分类树的话残差无法定义。针对每一个类别都用样本构建一个回归树,输入样本是相同的,唯一不同的就是标签值。预测的时候将样本放到所有回归树中,因此会有k个预测值,k为类别个数。再利用sigmoid将k个预测值转换成概率值。
4.2 XGBoost如何给出特征重要性
通过对每个特征记录其被决策树的使用情况,加权之后排序得到的。权重包括:分裂点离根节点越近,权重越高。被越多树选择,权重越高。
5. 深度神经网络(BN,dropout)
BN是为了防止激活函数失效建立的。在神经网络的某一层运算结束进入激活函数前,有可能某些单元的值远远偏离0,这些单元在之后的训练中起的用处并不大,因为激活函数对其微小的扰动已经不敏感。因此可以对隐藏层中进入激活函数前的值进行归一化,令其重新归于0附近,使激活函数有效运作。
但是归一化之后有可能会让数据失去原来的特征,并且有些激活函数(tanh,sigmoid)其在0附近是接近线性的。因此在归一化之后还要进行去归一化,通过学习两个参数 β , γ \beta ,\gamma β,γ,让已经变成(0,1)分布的数据恢复成均值为 β \beta β,方差为 γ \gamma γ的数据。此处的 β , γ \beta,\gamma β,γ是网络需要学习的参数,而归一化时所用到的数据的均值和方差,是用mini-batch中的数据得出的。
这里就会产生另外一个问题,在测试阶段,测试集由于样本数目可能比较少,所以由测试集得出的均值和误差可能不准确,对于此种情况,有两种解决方法。
- 测试时每一个单元的均值和方差由训练集中的均值和方差给出。
- 利用指数加权平均来获取所有mini-batch的均值和方差的估计,再用此值来估算测试集的均值和方差,指数加权平均定义为:
X n = β X n − 1 + ( 1 − β ) θ n X_n=\beta X_{n-1}+(1-\beta)\theta_{n} Xn=βXn−1+(1−β)θn
其中X是加权后的值, θ \theta θ是当前值, β \beta β是待确认参数。
5.1 dropout
dropout方法比较简单,是DNN中一种防止过拟合的方式。在每次训练中按照一定概率随机丢弃将一些权重归零,使得网络在训练时不会对某一个节点存在很高的依赖。
具体地,对于某一层的节点,假设有以下式子
z = w 1 ∗ x 1 + w 2 ∗ x 2 + w 3 ∗ x 3 + w 4 ∗ x 4 z=w_1*x_1+w_2*x_2+w_3*x_3+w_4*x_4 z=w1∗x1+w2∗x2+w3∗x3+w4∗x4
其中 w i w_i wi是权重, x i x_i xi是前一层的输出向量。则如果添加了dropout,并且设置保留权重概率为0.5,那么4个权重可能就会随机剩下两个,此时式子可能就会变成(假设去掉了 w 2 , w 4 w_2,w_4 w2,w4)
z = ( w 1 ∗ x 1 + w 3 ∗ x 3 ) / 0.5 z=(w_1*x_1+w_3*x_3)/0.5 z=(w1∗x1+w3∗x3)/0.5
其中计算完毕后除以0.5是因为在测试阶段,是用整个网络来训练的,为了保持输出节点的大小一致,需要除以这个保留因子。
注意在每一个mini-batch中,权重都会更新一次,之后dropout会重新随机分配归0的节点,下一个mini-batch时归0的权重和之前的不一样,有助于构建一个健壮的网络
5.2 初始化方式
6. 评价体系(召回率,准确率,精确率,ROC,AOC,偏差方差,欠拟合,过拟合等)
准确率(accuracy)定义为分类器判断正确的样本(包括正例和负例)占所有样本的比值,比如样本有50个正例和50个负例,现在分类器对其预测时,50个正例正确预测出40个,负例同样也是预测出40个,那么这个分类器的准确率就是80%。
当样本非常不均衡时,准确率的参考意义不大,比如说1百万个样本有1万个是负例,其余是正例,那么分类器只要把所有样本预测为正例,就可以获得99%的准确率,但是这个分类器没有意义。
精确率(Presicion)定义为,预测为正例的样本中,真正为正例的比例。
召回率(Recall)定义为,所有正例样本中,被预测为正例的比例。
很明显,在上方提到的样本中,负例召回率就是0,因为负例全部都没有被预测出来,而准确率和精确率都达到了99%。
还有个评价指标是F1值,是精确率和召回率的调和平均
1 F = 1 R + 1 P \frac{1}{F}=\frac{1}{R}+\frac{1}{P} F1=R1+P1
ROC曲线
ROC为曲线用于判定模型的表现具有很大参考意义。对于二分类模型,如果分类器输出的是对应样本的分数,而不是直接输出类别,那么可以用ROC来对其表现评分。
ROC曲线的Y轴是真正例率,定义为所有正例中能够被分类器挑出的比例。X轴是假正例率,定义为所有负例中被分类器认为是正例的比例。
当分类器对测试集输出值为一个[0,1]的实数时,可以将阈值K从0开始慢慢增大,小于K的判定为负例,大于K的判定为正例,由此可以得到一系列的真正例率和反正例率,将它们连成一条曲线,即为这个分类器的ROC曲线
当一个分类器的ROC曲线在另一个分类器上方时,可以认为前者性能较好。但是实际上情况可能为两个分类器的曲线有交叉的部分,此时就要用到AOC(曲线下面积)进行比较,一般认为面积越大的分类器性能越好。
偏差和方差
偏差描述的是分类器的预测值与真实值的偏离程度,反映的是分类器的拟合能力,如果分类器欠拟合,那就证明还没有真实学习到样本特征,自然预测的时候就会出现偏差。
方差描述的是训练集的变动对学习性能的变化,反映了数据扰动造成的影响。如果分类器过拟合,那么当训练样本有一个微小变动,本来对其总体特征应该不会有太大影响。但是分类器的预测可能会造成较大的变化。
解决方法:对于欠拟合,可以用添加特征数量,增加训练时间,增加模型复杂度来解决。
对于过拟合,情况会更复杂,只能在一定程度上抑制过拟合。采用的方法包括,添加正则化项,降低模型复杂度,提前终止训练,增加样本数量,交叉检验等。
其中正则化方法包括L1正则化和L2正则化,分别指权值向量的一阶和二阶范数。对于L1正则化,其能够让权值向量倾向于稀疏化,即产生很多0值的权重,这在文本处理中用得较多。对于L2正则化,其倾向于让权值更加接近0。
7.激活函数的特点
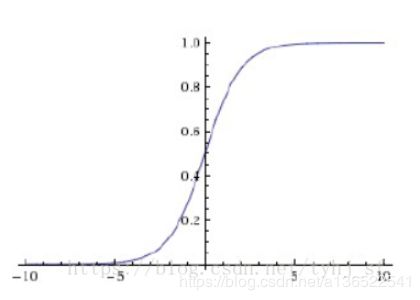
首先是sigmoid函数,其数学形式如下
f ( z ) = 1 1 + e x p ( − z ) f(z)=\frac{1}{1+exp(-z)} f(z)=1+exp(−z)1
其能够把输入的变量转化为一个0-1的实数,当输入趋向正无穷,输出趋向1,出入趋向服务器,输出趋向-1。sigmoid函数曾经用得很多,但是其有不少缺点
tanh函数形式和图像如下:
f ( z ) = e x p ( z ) − e x p ( − z ) e x p ( z ) + e x p ( − z ) f(z)=\frac{exp(z)-exp(-z)}{exp(z)+exp(-z)} f(z)=exp(z)+exp(−z)exp(z)−exp(−z)
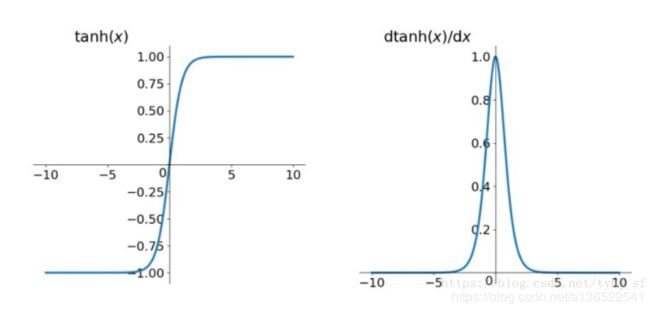
其图像与sigmoid类似,只是输出[0,1]的实数变为输出[-1,1]的实数,运算速度慢以及梯度消失的问题依然存在
Relu函数,图像如下
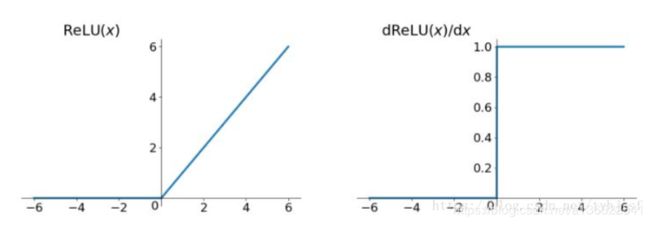
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
其函数形式非常简单,注意其并在0点是不可导的。其一定程度上解决了梯度消失的问题,其运算也简单,收敛速度也快。
Relu主要有的问题就是有可能有些神经元永远不会被激活(因为其值小于0),存在的原因可能是因为初始化参数设置不好,或者学习率太大使权重进入了这个状态,解决方法是可以用Xavier初始化或者用一些能够更新学习率的优化方法。以及使用LeakRelu方法,在x<0时,并不将其置0,而是设置为 α X \alpha X αX,其中 α \alpha α为一个小数,通常设为0.01。
8. SVM等知识(多分类,核函数)
SVM的目的是在特征空间中找到一个超平面,将样本分成不同的类,超平面可以用 w ⋅ x + b = 0 表 示 w\cdot x+b=0表示 w⋅x+b=0表示,也可以简写为(w,b)。一般来说这个超平面有无数多个,而SVM要求样本中离超平面最近的点间隔最大,因此这个超平面只有一个。
首先样本 ( x i , y i ) (x_i,y_i) (xi,yi)到超平面 ( w , b ) (w,b) (w,b)的函数间隔可以用以下式子定义:
γ ^ i = ( w ⋅ x i + b ) \hat\gamma_i=(w\cdot x_i+b) γ^i=(w⋅xi+b)
不难发现,当(w,b)成比例地放大缩小时,超平面是不会变化的,但是函数间隔同样会成比例放大缩小,因此需要固定超平面的格式,使样本到超平面的距离成为一个可以量度的量,因此引入几何间隔:
γ i = 1 ( ∣ ∣ w ∣ ∣ ) ( w ⋅ x i + b ) \gamma_i=\frac{1}{(||w||)}(w\cdot x_i+b) γi=(∣∣w∣∣)1(w⋅xi+b)
其中||w||是向量w的二阶范数。
因此SVM的目标问题转化为数学形式后可以表达为
max w , b γ ∣ ∣ w ∣ ∣ ^ \max \limits_{w,b}\hat\frac{\gamma}{||w||} w,bmax∣∣w∣∣γ^
要求 y i ( w ⋅ x i + b ) ≥ γ ^ i = 1 , 2... N y_i(w\cdot x_i+b)\ge \hat\gamma \qquad i=1,2...N yi(w⋅xi+b)≥γ^i=1,2...N
i=1,2…N是对所有样本计算,约束条件中要求所有样本的函数间隔都大于 γ ^ \hat\gamma γ^。在此问题中,因为当w,b成比例变化时,||w||, γ ^ \hat\gamma γ^,都会同时成比例变化,所以 γ ^ \hat\gamma γ^的取值对于上述问题是没有影响的。简单起见就将其设置为1,因此上述问题可以化为
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min \limits_{w,b}\frac{1}{2}||w||^2 w,bmin21∣∣w∣∣2
s . t . y i ( w ⋅ x i + b ) ≥ 1 s.t.\qquad y_i(w\cdot x_i+b)\ge1 s.t.yi(w⋅xi+b)≥1
要解决这个问题,可以引入拉格朗日乘子 α i ≥ 0 \alpha_i\ge0 αi≥0
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 n α i y i ( w ⋅ x i + b ) + α i L(w,b,\alpha)=\frac{1}{2}||w||^2-\sum_{i=1}^{n}\alpha_iy_i(w\cdot x_i+b)+\alpha_i L(w,b,α)=21∣∣w∣∣2−i=1∑nαiyi(w⋅xi+b)+αi
问题可以化为,先求L对 α \alpha α的极大值,再对w,b求极小值。
经过复杂求解过程后,分类决策函数可以写成
f ( x ) = s i g n ( ∑ i = 1 n α i y i ( x ⋅ x i ) + b ) f(x)=sign(\sum_{i=1}^{n}\alpha_iy_i(x\cdot x_i)+b) f(x)=sign(i=1∑nαiyi(x⋅xi)+b)
其中 x i x_i xi是样本向量,x是输入向量,可以看到决策函数只决定于输入向量和样本向量的内积。
注意上述解答是针对于样本完全线性可分的,在实际情况中,由于样本可能存在噪声,样本可能不能完全线性可分,也不应该要求分类器能够完全正确把噪声正确分类。因此可以对每个样本 ( x i , y i ) (x_i,y_i) (xi,yi)引入一个松弛变量 ξ i \xi_i ξi,使函数间隔加上 ξ i \xi_i ξi后大于1
y i ( w ⋅ x i ) + ξ i ≥ 1 y_i(w\cdot x_i)+\xi_i\ge1 yi(w⋅xi)+ξi≥1
同时对于每一个 ξ \xi ξ,都要支付一个代价,因此目标函数可以化为
1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i \frac{1}{2}||w||^2+C\sum_{i=1}^n\xi_i 21∣∣w∣∣2+Ci=1∑nξi
其中C为惩罚系数,用于权衡两项的比例关系,当C越大时,越要求分类器能够把样本完美分类。
对于线性不可分的样本,需要用核技巧进行处理,将样本变换为线性可分的空间中。
核函数
通过将输入样本和训练样本的内积 x ⋅ x i x\cdot x_i x⋅xi转化为核函数,可以把样本投射到高维空间中,在高维空间找对应分割超平面,从而解决一些非线性问题,常用的核函数有多项式核函数
K ( x , x i ) = ( x ⋅ x i + b ) p K(x,x_i)=(x\cdot x_i+b)^p K(x,xi)=(x⋅xi+b)p
高斯核
K ( x , x i ) = e x p ( − ( x − x i ) 2 σ 2 ) K(x,x_i)=exp(-\frac{(x-x_i)^2}{\sigma^2}) K(x,xi)=exp(−σ2(x−xi)2)
作变换之后,分类决策函数可以写成
f ( x ) = s i g n ( α i y i K ( x , x i ) + b ) f(x)=sign(\alpha_iy_iK(x,x_i)+b) f(x)=sign(αiyiK(x,xi)+b)
一般情况下高斯核函数是比多项式核有效。相比于多项式核,高斯核函数能够将样本映射到无穷维空间,原因可以用泰勒公式说明
e x = ∑ i = 1 n x n n ! e^x=\sum_{i=1}^{n}\frac{x^n}{n!} ex=i=1∑nn!xn
多分类问题
SVM是针对二分类问题的,如果要解决多分类问题,假设样本类别为 k 1 , k 2 . . . . k n k_1,k_2....k_n k1,k2....kn一共有k个,可以有2种方法间接实现。
1.可以先训练一个分类器F1,将类别 k 1 k_1 k1挑出来。剩下的样本训练分类器 F 2 F2 F2,将类别 k 2 k_2 k2挑出来。一直进行下去直到类别挑选完成,一共需要k-1个分类器。
2.对于任意两个类别 k a , k b k_a,k_b ka,kb都训练一个分类器,最终用投票来选择样本最终的类别,但是此种情况下的分类器数量是 N 2 N^2 N2数量级的,如果类别有1000个的话,对于性能影响太大。所以实际操作时一般会采取第一种方式。
LR和SVM的区别
1.损失函数不一样,LR的是最小化交叉熵损失函数,SVM是最大化间隔距离
2.SVM只考虑位于超平面最近的几个点,在此之外添加和删除数据没有影响。而LR中每一个样本数据都可能对结果产生影响。
3.LR可以输出样本属于某一类的概率,而SVM不能,其只能够给出类别值
9.新型方法(GAN,LSTM,目标检测,TensorFlow2.0)
GAN
GAN现在能够用于图像、语音、文本中。GAN主要包含一个生成模型和判别模型。在图片领域里,生成模型是生成一张看起来真实的图片,而判别模型是需要正确判别图片是真实的还是生成。两者经过不断博弈之后不断改进自身,直到判别模型无法判断图片是真实的还是生成的,两个模型达到最优。
在图像识别中,可以用CNN来提取图片的信息进行识别。在生成模型中,则需要反过来,用反卷积,将噪声经过一个与CNN相反的结构,生成逼真的图片。
GAN现在在生成逼真的图片上已经做得十分理想,能够生成人类可能无法识别的人脸,或者场景照片等。在需要大量样本训练的模型中,比如说自动驾驶,可以用GAN生成的数据去训练,达到理想的效果
GAN目前遇到的问题是,无法用客观的标准去认定生成图片的好坏。如何用GAN去处理其他问题,比如机器翻译,对话语音生成等。
LSTM
LSTM是一种特殊的RNN,主要问了解决长序列训练中梯度消失和梯度爆炸问题。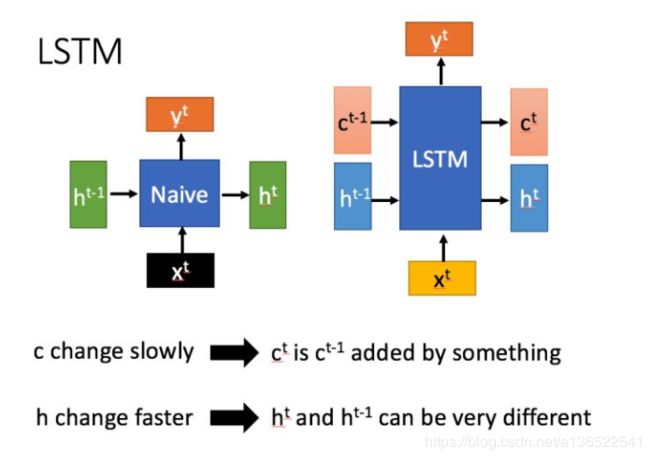
左图是普通的RNN,输入是前一个单元输出的状态 h t − 1 h_{t-1} ht−1和当前状态 x t x_t xt,经过运算之后会输出一个Y值和下一个单元的输入值 h t h_t ht。
右图是LSTM的结构,传入状态有两个 c t − 1 , h t − 1 c_{t-1},h_{t-1} ct−1,ht−1,其中 c t c_t ct变化较慢, h t h_t ht变化较快,运算结束之后输出 c t , h t c_t,h_t ct,ht
LSTM主要通过门控来控制传输状态,记住那些需要长时间记忆的,忘记不重要的信息,而不像普通RNN一样只能有一种记忆方式。
但是因为引入了更多的参数,导致训练难度也加大了。