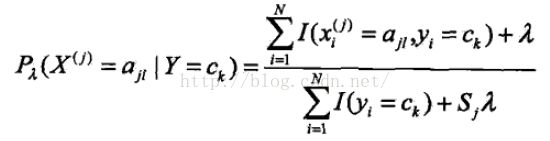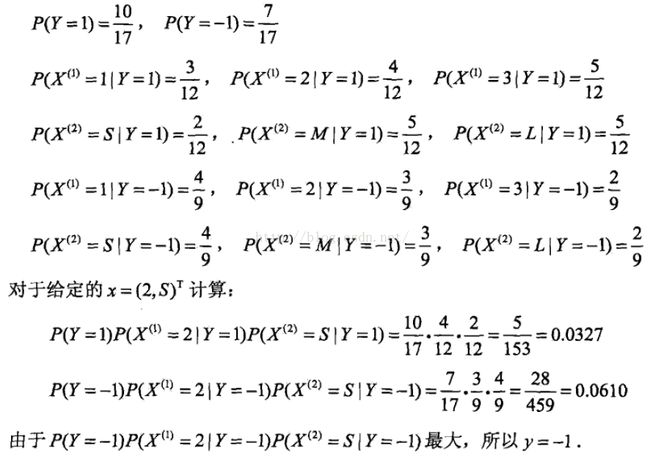机器学习——朴素贝叶斯法（naive Bayes）

         朴素贝叶斯的原理再此就不细说了，有兴趣的朋友参看《统计学习方法》，里面给出详细的说明。本文仅给出算法，同时做出少量解释，然后给出python的实现。

        下面给出相应的算法描述

         在输入中，训练数据的每个元素由特征X和标签Y组成，特征X是一个包含n个x元素的列向量。

         第一步：计算先验概率和条件概率。

                   公式一：计算标签为Ck的情况的概率，I()表示计数过程，符合条件为1，不符合为0

                   公式二：计算当标签为Ck时，特征X中的元素为a的情况的概率，此处用到了贝叶斯概率公式

          第二步：对于要预测的实例x，计算x属于标签ci，x的每个元素都满足的情况（注意：这不是条件ci下x的概率，解释见《统计

                          学习方法》）

                   Ri = 标签为ci的概率 × 特征完全符合x的概率

          第三步：从第二步计算所有标签的Ri，排序得到最大的Ri，则x的标签与Ri的标签相同。

        在算法的第一和第二个公式中，分子可能出现为0的情况，这样对计算产生影响，此时采用贝叶斯估计的方法解决。其实就是将上述两个公式稍加修改，当lambda取1时，称为拉普拉斯平滑。

        这个修改非常好理解，《统计学习方法》中又一道题如下：

        人工计算过程如下：

       

        下面给出代码实现：

#!/usr/bin/env python
# encoding: utf-8
X_data = [[1,'S'],[1,'M'],[1,'M'],[1,'S'],[1,'S'],[2,'S'],
          [2,'M'],[2,'M'],[2,'L'],[2,'L'],[3,'L'],[3,'M'],
          [3,'M'],[3,'L'],[3,'L']]
Y_label = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1]

def prior_probability(Y_label,la):# la= lambda 计算先验概率
    count = 0
    for i in range(len(Y_label)):
        if Y_label[i] == 1:
            count += 1

    positive = 1.0 * ( count + la )/( len(Y_label) + 2*la ) # only 2 kind labels
    negtive = 1 - positive
    prior = [positive,negtive]
    return prior


def condition_probablity(X_data,Y_label,la): #计算条件概率
    count = 0
    count_Y = 0
    m = 0
    n = 0
    table = [[0 for i in range(6)] for y in range(2)] #将结果存到表格中，为了简化，对应的列顺序为1,2,3，L，M，S，行顺序为1，-1.
    for y in [1,-1]:
        for i in range(len(Y_label)): 
            if Y_label[i] == y:
                count_Y += 1
        for x in [1,2,3,'L','M','S']:
            for i in range(len(X_data)):
                if Y_label[i]==y and (X_data[i][0]==x or X_data[i][1] == x):
                    count += 1
            pro = 1.0 * (count + la) / ( count_Y + 3*la ) # x 的每一维只有3种元素
            count = 0
            table[m][n] = pro
            n += 1
        count_Y = 0
        m += 1
        n = 0
    return table

def get_label(x1,x2,prior,condition_pro):
    pro1 = prior[0] * condition_pro[0][x1]*condition_pro[0][x2]
    pro2 = prior[1] * condition_pro[1][x1]*condition_pro[1][x2]
    if pro1 > pro2:
        return '1'
    else:
        return '-1'

prior = prior_probability(Y_label,1)
condition_pro = condition_probablity(X_data,Y_label,1)
label = get_label(1,5,prior,condition_pro)#x的两个特征为2和S，在表格中为第1和5列，为了简化直接人工输入，当数据很多的时候，建议在编程之前设计好数据结构
print label

          本代码只给出最后的预测标签，其实读者可以根据需要自行打印各个阶段的结果。代码中为了简便，列表的列是人为指定数字来代替的，如果读者希望能使用其本身的数字和字母来表示，可以在最开始的时候将data转化成矩阵，使用以下代码即可

df = pd.dataFrame(data)
df.colums = [1,2,3,'L','M','S']