导航路径规划之五 A*算法
A*算法是启发式搜索,是一种尽可能基于现有信息的搜索策略,也就是说搜索过程中尽量利用目前已知的诸如迭代步数,以及从初始状态和当前状态到目标状态估计所需的费用等信息。
A*算法可以选择下一个被检查的节点时引入了已知的全局信息,对当前结点距离终点的距离作出估计,作为评价该节点处于最优路线上的可能性的量度,这样可以首先搜索可能性大的节点,从而提高了搜索过程的效率。
A*算法的基本思想如下:引入当前节点j的估计函数f*,当前节点j的估计函数定义为:
f*(j)= g(j)+h*(j)
其中g(j)是从起点到当前节点j的实际费用的量度,h*(j)是从节点j到终点的最小费用的估计,可以依据实际情况,选择h*(j)的具体形式,h*(j)要满足一个要求:不能高于节点j到终点的实际最小费用。从起始节点点向目的节点搜索时,每次都搜索f*(j)最小的节点,直到发现目的节点。
A*算法的核心是设计估价函数,设计估价函数h(j)有很多方法,下面介绍其中的两种。
估价函数1:欧几里德距离
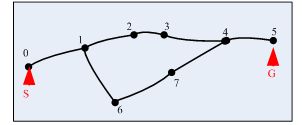
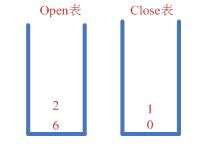
可以证明,在和起点距离相等的中间节点集合里,与终点直线距离(欧几里德距离)越小的节点,方向夹角越小。假设在图2-3求S到G点的最短路径,与S最近的点是节点2,与G最近的是节点11,因此可以确定上路点是节点2,下路点是节点11,求S到G点的最短路径就是求节点2到节点11的路径。定义L(i,j)表示从节点i到节点j的有向线段,Angle[ L(I,j),L(a,b) ]表示有向线段ij和有向线段ab的夹角。由于Angle[ L(2,11),L(2,3) ]< Angle[L(2,11),L(2,1) ] ,因此选择节点3,而与节点3连接的节点有节点4和节点7,Angle[ L(3,11),L(3,7) ]< Angle[ L(3,11),L(3,4) ],选择节点7,与节点7相连的节点有节点8,节点11,和节点6,由于Angle[L(7,11),L(7,11) ]< < Angle[ L(7,11),L(7,6) ] 假设起点S的坐标(Sx,Sy),终点G的坐标(Gx,Gy),中间点N的坐标(Nx,Ny), 估价函数取欧几里德距离,表示为: 这个估价函数的计算量很大,不利于海量数据的路径规划计算。 估价函数2:曼哈顿距离 利用欧几里德距离计算估价函数的计算量很大,因此考虑将两点之间的曼哈顿距离作为估价函数。其中A点的经纬度为(Ax,Ay),B点的经纬度是(Bx,By),则A、B之间的Manhattan距离可以表示为: M(A,B)=P*(|Ax-Bx|+|Ay-By|) P = 2*∏*R / 360 由于P是常数,可以简化为 f(j)=g(j)+(|Ax-Bx|+|Ay-By|) 此估价函数计算量小,虽然不是严格的方向优先,但基本能保证最短路径的搜索方向向目标点的方向进行。 A*算法在搜索中设置两个表:Open表和Close表。Open表保存了所有已生成而未被考察的节点,Close表中记录已被考察过的节点。算法中有一步是根据估计函数重排Open表中的节点,这样,循环的每一步只考虑Open表中状态最好(代价最小)的节点,如果被发现在Open表中存在同一个节点,就应比较两个节点代价的大小,如扩展得到的新节点代价大于已有的节点代价,可以放弃扩展得到的新节点,否则就以新节点代替原来的节点。如果在Close表中存在同一个节点号,则新新生成的路径的代价肯定大于原来路径的代价,可以淘汰新生成的节点。 算法步骤如下: 步1:生成空的Open表、Close表,将起点S放入Open表 步2:如果Open表为空,则失败退出。 步3:从Open表中,找出头节点U,作为当前节点,将它从OPEN表中移除。 步4:判断U是否为终点,如果是,则通过节点U的父指针,一直遍历到起点,找到到最优路径,算法结束。否则,转步5. 步5:扩展当前节点U,找到其扩展的后继节点集合V,遍历集合V中的节点,如果节点即不在Open表也不在Close表,计算该节点的估计值,将节点加入到OPEN表,设置父节点为U.如果节点在Open表、Close表,比较当前节点的代价g(v)和Open表、Close表中代价,如果当前节点的代价g(v)小,更新表中的代价和父节点指针。 步6:按估价值递增的顺序,对Open表中所有节点进行排序。 步7:转步2. 举一个例子来说。有路网如下图,假设需要从S节移动到G节点,则A*算法的计算过程如下: 1)初始状态:设置节点0的f(x)=0, 节点0进Open表,寻路成功标志bFind为false;设置Close表为空。 2) 估算节点0,考察与节点0相连的所有节点(只有节点1)是否是目标节点,如果不是则估算这些节点的f(x)值,将其放进Open表,同时节点0被放入Close表;最后需要将open表中的节点按f(x)的值从小到大的顺序排列。 3)从Open表取出f(x)值最小的节点(节点1),考察与节点1相连的所有节点(节点2,6)是否是目标节点,如果不是则估算这些节点的f(x)值,将其放进Open表,同时节点1被放入Close表。最后需要将open表中的节点按f(x)的值从小到大的顺序排列(由于节点2比节点6接近目标节点,因此节点2的f(x)值小于节点6的f(x)值,节点2排在节点6的前面)。 4) 从Open表取出f(x)值最小的节点(节点2),考察与节点2相连的所有节点(节点3)是否是目标节点,如果不是则估算这些节点的f(x)值,将其放进Open表,同时节点2被放入Close表。将open表中的节点按f(x)的值从小到大的顺序排列。 5)从Open表取出f(x)值最小的节点(节点3),考察与节点3相连的所有节点(节点4)是否是目标节点,如果不是则估算这些节点的f(x)值,将其放进Open表,同时节点3被放入Close表。将open表中的节点按f(x)的值从小到大的顺序排列。 6)从Open表取出f(x)值最小的节点(节点4),考察与节点4相连的所有节点(节点5)是否是目标节点,如果是则将节点4被放入Close表,然后将考察的节点(节点5)放入Close表,此时发现一条丛开始地到目的地的路径。 7) 从节点5开始往前回溯,从Close表中提取路径。 根据以上思路,A*算法的伪代码如下:
A*()
{
Open = [起始节点];
Closed = [];
while (Open表非空)
{
从Open中取得一个节点X,并从OPEN表中删除。
if (X是目标节点)
{
求得路径PATH;
返回路径PATH;
}
for (每一个X的子节点Y)
{
if (Y不在OPEN表和CLOSE表中)
{
求Y的估价值;
并将Y插入OPEN表中;
}
//还没有排序
else if (Y在OPEN表中)
{
if (Y的估价值小于OPEN表的估价值)
更新OPEN表中的估价值;
}
else //Y在CLOSE表中
{
if (Y的估价值小于CLOSE表的估价值)
{
更新CLOSE表中的估价值;
从CLOSE表中移出节点,并放入OPEN表中;
}
}
将X节点插入CLOSE表中;
按照估价值将OPEN表中的节点排序;
}//end for
} //end while
} //end function