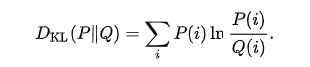数学之美 阅读笔记
数学之美是通过作者在学校或谷歌等公司的学习和工作经历,根据具体的工程项目,介绍其基本原理和背后的数学支持的一本书。例如:文本的分析和马尔可夫模型,搜索引擎的索引和布尔代数,新闻的分类和余弦定理、奇异值分解。它们之间到底有什么样的关系呢?让我们走近这本书中一探究竟。
一开始写这篇文章,只是出于兴趣……但是后来才发现,如果想要从头到尾认真地读完并做好记录,并不是一件简单的事,中途几次想要放弃,最后还是坚持利用碎片时间重读了好几次(第一次只是简单地看完了全书,后来想写阅读总结时才发现读一遍是不够的),并在手机上做笔记,有空了再把它们转移到电脑上编辑一下,有些地方还有疏漏,并没有涵盖到所有作者讲到的内容。但是这本书已经给了我很多有用的东西,不管是科学方面还是研究方法,甚至是人生哲学方面……是时候做一个告别,开始下一段读书之旅了。
资源推荐:穿越虫洞是作者在后记中提及的对自己非常有帮助的节目。还有霍金的时间简史和伽莫夫的从1到无穷大。这些资料的特点都是深入浅出地讲解深奥的物理或宇宙原理,可以让人从思想上领略物质运作规律。
1.统计语言模型和自然语言处理
一个句子是否合理,就看看它的可能性大小如何。——贾里尼克
自然语言处理的第一个难题:传统的基于规则的句法分析局限性:词语的多义性难以用规则描述,严重依赖上下文,由常识所依赖的理解依然不能通过上下文来解决。
而由贾里尼克提出的统计语言模型是利用自然语言上下文相关的特性建立的数学模型。让计算机利用大量的数据通过统计模型进行建模。这种应用统计方法的思想的核心是,通信系统加隐含马尔可夫模型。目前已应用于机器翻译,语音识别,手写体识别,拼写纠错,汉字输入,文献查询,等需要语言理解的地方。
消除不确定性的方法是从外部引入信息。例如网页搜索,就是通过用户给出的关键词来消除不确定性。如果关键词所引入的信息量不够,则应该挖掘新的信息,而不是引入人为的假设,玩弄各种公式和机器学习算法。应该学会合理利用信息。
由公式 H ( X ) > = H ( X ∣ Y ) > = H ( X ∣ Y , Z ) H(X)>=H(X|Y)>=H(X|Y,Z) H(X)>=H(X∣Y)>=H(X∣Y,Z)知,引入新的条件,会在一定程度上消除信息的不确定性,引入的条件越多,不确定性下降的越多,前提是:获取的条件信息要和研究的事物有关系。因此,也证明了二元模型比一元模型好,三元模型比二元模型好。自然语言处理的大量问题就是找相关的信息。
相对熵(又称KL散度)则用来衡量两个函数的相似性,公式如下。特别的,如果函数为概率密度函数,则可以度量两个随机分布的差异性。相对熵越大,两个函数的差异越大。例如:两个词是否同义就看它们在文档中的分布频率,判断两篇文章内容是否相近。
小结:统计语言模型是基于概率统计,信息论的一种语言模型,简单来说就是通过上下文给出某个位置概率最大的词的建模方法。模型的建立还依赖于相关信息的引入,巨大的统计样本空间(大数据),和各种定理原理(如马尔可夫假设,贝叶斯公式,信息熵,大数定理等等)。
2.搜索引擎相关技术
人们发觉真理在形式上从来是简单的,而不是复杂和含混的。-——牛顿
搜索引擎最基本的三个技术是下载,索引和排序。下载是指在有限的时间内利用图论思想下载尽可能多的网页。索引是指基于词汇表对所有网页建立一个巨大的索引表。排序是指基于网页的被链接次数(表明了该网页的质量)和查询与网页的相关性对所有被索引到的网页进行排序。
利用图论进行网页的下载
如何下载所有网页,采用的是图论的原理。把每个网页视为一个节点,而超链接则是链接网页的弧。自动访问每个网页并保存的程序是网络爬虫。
在遍历网页时,深度优先还是广度优先?首先要下载所有的重要网页(一般是网站首页),所以是基于广度优先;考虑到握手次数(下载服务器和网站服务器建立通信的过程)尽量少,在每个网站间应使用深度优先。
利用布尔代数建立索引
通过对每个关键词,判断所有的网页是否含有该关键词,对向量的相应位置置1或0,这样,每个词对应一个向量,而词汇表中的所有词的向量就组成了一张大的矩阵。搜索时,对关键词(如我们输入数学之美,书这两个词)的向量进行AND布尔运算,得出值为1的位置代表含有搜索关键词的网页。
网页排序技术
pagerank 网页排名取决于网页的质量信息和查询与网页的相关性信息。
对一个网页的排名通过指向这个网页的所有网页权重之和来计算。权重源于这些网页自身排名。我们首先初始化排名(也表示权重),然后将其乘以链接数矩阵,经过多次迭代,使排名逐渐收敛于一个稳定值。
词频率-逆向文档频率(TF-IDF):
要看关键词和要搜索的网页是否相关,我们通常会看它在某个网页文本中出现的频率TF,越高则相关性越强。(例如,“数学之美”在一个网页中出现多次,则这个网页很可能是我们要查询的网页)
另一方面,我们要看这个词语的特殊程度(例如,“的”和“数学之美”),两个词可能在文本中出现的频率相同,但它们的作用却大不相同(我们希望“的”的权重小一些,而“数学之美”的权重大一些)。因此,使用IDF=log(D/DW)表示相关性。D为所有网页数,DW为出现该词语的网页数,IDF的值越大,则说明这个词越倾向于出现在更少的网页中,这个词的作用越大。从信息论的角度来看,TF-IDF代表了对一个词的信息量大小的度量。
新闻分类技术
余弦定理和新闻分类:一篇新闻可以通过每个词语的TF-IDF值转化为一串数字,也就是一个向量,然后用余弦定理计算向量夹角,来衡量新闻相似度。其实就是衡量两篇新闻里每个词语出现的频率,是否一致。
新闻分类的另一种方法是利用矩阵理论里的奇异值分解,这种方法相比余弦定理更为快速,但占用的存储空间更大,且分类结果比较粗糙。原理是将一个较大的矩阵(每行代表一个文本,每列代表词语的TF-IDF值)分解为三个较小矩阵的乘积。
总结:在计算机科学领域,一个好的算法应该简单,有效,可靠性好而且容易读懂,易操作。在工程领域,先帮助用户解决百分之八十的问题,再慢慢解决剩下的百分之二十的问题,是在工业界成功的秘诀之一。因此,我们应当多实践,先有一个整体框架,然后在这个基础上不断完善,如果一开始就追求完全正确,毫无瑕疵,那可能永远也无法开始。
3.信息指纹
信息指纹的概念类似于对信息的编码,不同的是我们并不需要从信息指纹中无损地恢复出信息。信息指纹用来区别一段信息和其他信息。通常用一串随机数来表示。
只要生成随机数的算法足够好,就能保证几乎不可能出现重复的信息指纹。信息指纹的应用有:
1.将网页的URL映射到信息指纹上,将信息指纹存入哈希表,以判断一个网页是否被下载过。这样用信息指纹代替URL字符串被存储,可以极大地节省存储空间。
2.判断两首音乐是否相同,可以比较它们的信息指纹。判断两个集合里元素的信息指纹之和,如果相同,则为相同集合。信息指纹其实是以极小的错误概率代价来换取时间复杂度或存储的减小。
3.利用它的不可逆性,还可以进行网络加密。
总结:本小结以数学模型的重要性作为收尾。吴军博士总结了如下几点:
1 一个好的数学模型在形式上应该是简单的
2 一个正确的模型可能一开始并不如一个错误的模型准确,但是如果我们认为思路是对的,就应该坚持下去。
3 正确的模型可能由于种种原因而显得不准确,这是我们不应该用自己也不懂的凑合方法来修正,而是应该找到噪音的根源,这也许能指引我们通向新的发现。
4 注重知识和数据的积累。