《程序设计与算法》之【分治算法】

• 分治的基本概念
• 归并排序
• 快速排序
• 例题
  
  • 输出前m大的数
  • 求排列的逆序数

分治的基本概念

把一个任务，分成形式和原任务相同，但规模更小的几个部分任务（通常是两个部分），分别完成，或只需要选一部完成。然后再处理完成后的这一个或几个部分的结果，实现整个任务的完成。

分治的生活实例–称假币

16枚硬币，有可能有1枚假币，假币比真币轻。有一架天平，用最少称量次数确定有没有假币，若有的话，假币是哪一枚。

• 8 - 8一称，发现无假币，或者假币所在的那8枚
• 4 - 4一称
• 2 - 2一称
• 1 - 1一称

归并排序

数组排序任务可以如下完成：

1）把前一半排序
2) 把后一半排序
3) 把两半归并到一个新的有序数组，然后再拷贝回原数组，排序完成。

#include 
using namespace std;
/* 
 将数组a的局部[s,m]和a[m+1,e]合并到tmp，并保证tmp有序，然后拷贝回a[s,m]
 归并操作时间复杂度：O(e-m+1)，即O(n)
 */
void Merge(int a[], int s, int m, int e, int tmp[]) {
    int pb = 0;
    int p1 = s, p2 = m+1;
    while (p1 <= m && p2 <= e) {
        if (a[p1] < a[p2])
            tmp[pb++] = a[p1++];
        else
            tmp[pb++] = a[p2++];
    }
    while (p1 <= m)
        tmp[pb++] = a[p1++];
    while (p2 <= e)
        tmp[pb++] = a[p2++];
    for (int i = 0; i < e-s+1; i++)
        a[s+i] = tmp[i];
}
void MergeSort(int a[], int s, int e, int tmp[]) {
    if (s < e) {
        int m = s+(e-s)/2;
        MergeSort(a, s, m, tmp);
        MergeSort(a, m+1, e, tmp);
        Merge(a, s, m, e, tmp);
    }
}

int main() {
    int a[10] = {13, 27, 19, 2, 8, 12, 2, 8, 30, 89};
    int b[10];
    int size = sizeof(a)/sizeof(int);
    MergeSort(a, 0, size-1, b);
    for (int i = 0; i < size; i++) {
        cout << a[i] << " ";
    }
    cout << endl;
    return 0;
}

快速排序

数组排序任务可以如下完成：
1）设k=a[0], 将k挪到适当位置，使得比k小的元素都在k左边，比k大的元素都在k右边，和k相等的，不关心，在k左右出现均可 （O(n)时间完成）
2) 把k左边的部分快速排序
3) 把k右边的部分快速排序

#include 
using namespace std;
void swap(int &a, int &b) {
    int tmp = a;
    a = b;
    b = tmp;
}
void QuickSort(int a[], int s, int e) {
    if (s >= e)
        return;
    int k = a[s];
    int i = s, j = e;
    while (i != j) {
        while (j > i && a[j] >= k)
            j--;
        swap(a[i], a[j]);
        while (i < j && a[i] <= k)
            i++;
        swap(a[i], a[j]);
    }  // 处理完，a[i] = k
    QuickSort(a, s, i-1);
    QuickSort(a, i+1, e);
}
int main() {
    int a[10] = {13, 27, 19, 2, 8, 12, 2, 8, 30, 89};
    int size = sizeof(a)/sizeof(int);
    QuickSort(a, 0, size-1);
    for (int i = 0; i < size; i++) {
        cout << a[i] << " ";
    }
    cout << endl;
    return 0;
}

输出前m大的数

题目描述
给定一个数组包含n个元素，统计前m大的数并且把这m个数从大到小输出。

输入：
第一行包含一个整数n，表示数组的大小。n < 100000。
第二行包含n个整数，表示数组的元素，整数之间以一个空格分开。每个整数的绝对值不超过100000000。 第三行包含一个整数m，m < n。

输出：
从大到小输出前m大的数，每个数一行。

解答思路
排序后再输出，复杂度 O(nlogn)
用分治处理：复杂度 O(n+mlogm)
思路：把前m大的都弄到数组最右边，然后对这最右边m个元素排序， 再输出
关键 ：O(n)时间内实现把前m大的都弄到数组最右边

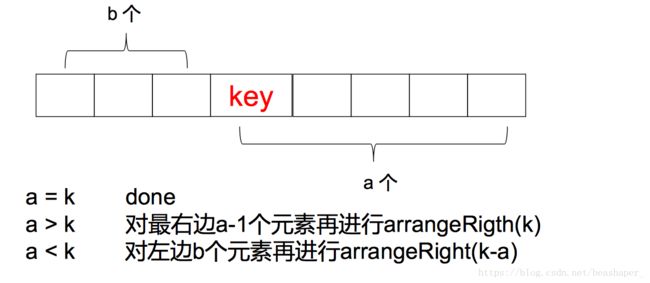
如何将前k大的都弄到最右边?

引入操作 arrangeRight(k): 把数组(或数组的一部分）前k大的 都弄到最右边
1）设key=a[0], 将key挪到适当位置，使得比key小的元素都在 key左边，比key大的元素都在key右边（线性时间完成）
2) 选择数组的前部或后部再进行 arrangeRight操作

解答

#include 
using namespace std;
void swap(int &a, int &b) {
    int tmp = a;
    a = b;
    b = tmp;
}
void QuickSort(int a[], int s, int e) {
    if (s >= e)
        return;
    int k = a[s];
    int i = s, j = e;
    while (i != j) {
        while (j > i && a[j] >= k)
            j--;
        swap(a[i], a[j]);
        while (i < j && a[i] <= k)
            i++;
        swap(a[i], a[j]);
    }  // 处理完，a[i] = k
    QuickSort(a, s, i-1);
    QuickSort(a, i+1, e);
}
void arrangeRight(int a[], int s, int e, int m) {
    if (s >= e)
        return;
    if (m == e-s+1)
        return;
    int k = a[s];
    int i = s, j = e;
    while (i != j) {
        while (j > i && a[j] >= k)
            j--;
        swap(a[i], a[j]);
        while (i < j && a[i] <= k)
            i++;
        swap(a[i], a[j]);
    }
    if (m == e - i + 1)
        return;
    else if (m < e - i + 1)
        arrangeRight(a, i+1, e, m);
    else if (m > e - i + 1)
        arrangeRight(a, s, i, m-(e-i+1));
}
void printM(int a[], int n, int m) {
    arrangeRight(a, 0, n, m);
    QuickSort(a, n-m, n-1);
}
int main() {
    int m = 5;
    int a[10] = {13, 27, 19, 2, 8, 12, 2, 8, 30, 89};
    int size = sizeof(a)/sizeof(int);
    printM(a, size-1, m);
    for (int i = size-m; i < size; i++) {
        cout << a[i] << " ";
    }
    cout << endl;
    return 0;
}

求排列的逆序数

题目描述
考虑1,2,…,n (n <= 100000)的排列i1 ，i2 ，…，in ，如果其中存在j，k，满足 j < k 且 ij > ik ， 那么就称(ij，ik )是这个排列的一个逆序。
一个排列含有逆序的个数称为这个排列的逆序数。例如排列 263451 含有8个逆序(2,1),(6,3),(6,4),(6,5),(6,1),(3,1),(4,1),(5,1)，因此该排列的逆序数就是8。
现给定1,2,…,n的一个排列，求它的逆序数。

解题思路
笨办法：O(n^2 )
分治O(nlogn)：
1） 将数组分成两半，分别求出左半边的逆序数和右半边的逆序数
2） 再算有多少逆序是由左半边取一个数和右半边取一个数构成(要求O(n)实现）
2) 的关键：左半边和右半边都是排好序的。比如，都是从大到小排序的。这样，左右半边只需要从头到尾各扫一遍，就可以找出由两边各取一个数构成的逆序个数

#include 
using namespace std;

int count_ = 0;

void Merge(int a[], int s, int m, int e, int tmp[]) {
    int pb = 0;
    int p1 = s, p2 = m+1;
    while (p1 <= m && p2 <= e) {
        if (a[p1] <= a[p2])
            tmp[pb++] = a[p2++];
        else {
            count_ += e-p2+1;
            tmp[pb++] = a[p1++];
        }
    }
    while (p1 <= m)
        tmp[pb++] = a[p1++];
    while (p2 <= e)
        tmp[pb++] = a[p2++];
    for (int i = 0; i < e-s+1; i++)
        a[s+i] = tmp[i];
}
void MergeSort(int a[], int s, int e, int tmp[]) {
    if (s < e) {
        int m = s+(e-s)/2;
        MergeSort(a, s, m, tmp);
        MergeSort(a, m+1, e, tmp);
        Merge(a, s, m, e, tmp);
    }
}

int main() {
    int a[10] = {13, 27, 19, 2, 8, 12, 2, 8, 30, 89};
    int b[10];
    int size = sizeof(a)/sizeof(int);
    MergeSort(a, 0, size-1, b);
    cout << count_ << endl;
    return 0;
}