【python】Leetcode(Data Structure / Algorithm)
文章目录
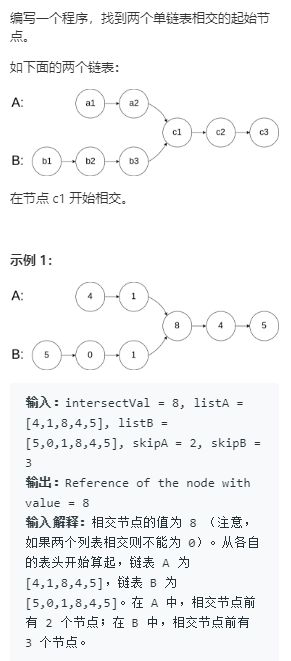
- 160. 相交链表(链表)
- 232. 用栈实现队列
- 69. x 的平方根(二分法)
- 215. 数组中的第K个最大元素(快排)
- 347. 前 K 个高频元素(桶排序)
- 378. 有序矩阵中第K小的元素(排序)
- 1051. 高度检查器(排序)
- 17. 电话号码的字母组合(递归)
- 241. 为运算表达式设计优先级(分治)
- 455. 分发饼干(贪心)
160. 相交链表(链表)
class Solution(object):
def getIntersectionNode(self, headA, headB):
"""
:type head1, head1: ListNode
:rtype: ListNode
"""
p = headA
q = headB
while(q!=p):
if p == None:
p = headB
else:
p = p.next
if q == None:
q = headA
else:
q = q.next
return p
232. 用栈实现队列
-
使用栈实现队列的下列操作:
push(x) – 将一个元素放入队列的尾部。
pop() – 从队列首部移除元素。
peek() – 返回队列首部的元素。
empty() – 返回队列是否为空。 -
示例:
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek(); // 返回 1
queue.pop(); // 返回 1
queue.empty(); // 返回 false -
说明:
你只能使用标准的栈操作 – 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)。
思路,用两个栈,一个负责输入(push),一个负责输出(pop)
class MyQueue(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.s1 = [] # 负责输入
self.s2 = [] # 负责输出
def push(self, x):
"""
Push element x to the back of queue.
:type x: int
:rtype: None
"""
self.s1.append(x)
def pop(self):
"""
Removes the element from in front of queue and returns that element.
:rtype: int
"""
if not self.s2: # 为空的话,把s1的元素逆序传进去s2
while self.s1:
self.s2.append(self.s1.pop())
return self.s2.pop() #返回 s2的栈顶元素,也就是 s1的栈底,也就是队头
def peek(self):
"""
Get the front element.
:rtype: int
"""
if not self.s2: # 思路和 pop 一样
while self.s1:
self.s2.append(self.s1.pop())
return self.s2[-1] # 返回 s2的栈顶元素,也就是 s1的栈底,也就是队头
def empty(self):
"""
Returns whether the queue is empty.
:rtype: bool
"""
return self.s1==[] and self.s2==[] # 当两个栈都为空的时候,队列为空!
# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()
69. x 的平方根(二分法)
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
-
示例 1:
输入: 4
输出: 2 -
示例 2:
输入: 8
输出: 2 -
说明: 8 的平方根是 2.82842…,
由于返回类型是整数,小数部分将被舍去。
1)暴力法
会超时
class Solution(object):
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
for i in range(x//2,-1,-1):
if i**2 == x:
return i
elif i**2>x>=(i-1)**2:
return i-1
2)二分法
这里比较别扭的是取整,和二分查找还不一样,x 的平方根大概率会落在两个数字之间,所以要对二分法做一些小改进 middle**2 <= x < (middle+1)**2
class Solution(object):
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
if (x==0): # 这一句也是相当重要的!
return x
start = 1
end = x
while(start <= end):
middle = (start + end)//2 # 注意二分法的计算中间值的时候要放在 while 里面
if middle**2 <= x < (middle+1)**2:
return middle
if middle**2 < x:
start = middle
if middle**2 > x:
end = middle
二分法的核心就是 while(start <= end),然后不断调整 start 和 end 来缩小搜索空间!!!
215. 数组中的第K个最大元素(快排)
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
-
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5 -
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4 -
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
1)调用 sorted
class Solution(object):
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
nums = sorted(nums)
return nums[-k]
2)快排
快排是对冒泡排序的一种改进,它的基本思想(分治)是,通过一趟排序,将待排记录分割成独立的两个部分,其中一个部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序!
先用快排排序,再挑选第 k 大的值
class Solution(object):
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
def partion(nums, left, right):
key = nums[left] # 注意这里基元素的选取,第一个元素,别写成了 nums[0]
low = left
high = right
while low < high:
while (low < high) and (nums[high] >= key): #右指针遇到小于基准元素的停下
high -= 1
nums[low] = nums[high] #右指针指向的值覆盖左指针
while (low < high) and (nums[low] <= key): # 左指针遇到大于基准元素的停下
low += 1
nums[high] = nums[low] # 左指针指向的值覆盖右指针
nums[low] = key # 用基值覆盖左右指针相逢的地方
return low # 返回左右指针相逢的地方
def quicksort(nums, left, right):
if left < right: #这句话超级关键
p = partion(nums, left, right)
quicksort(nums, left, p-1)
quicksort(nums, p+1, right)
return nums
return quicksort(nums,0,len(nums)-1)[-k]
注意 def quicksort 中的递归终止条件!def partion 中,扫描指针的两个 while 改变下符号,就可以从大到小排序 nums[high] <= key 和 nums[low] >= key
注意,while 的顺序
![]()
以 [5,7,3,8,1,9,2,0,6] 为例,可以看看 partion 的例子

3)堆排
……(bryant)
347. 前 K 个高频元素(桶排序)
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
-
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2] -
示例 2:
输入: nums = [1], k = 1
输出: [1] -
说明:
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
先回顾下最简单的 Bucket sort
res = []
nums = [2,8,3,2,3,8,3,4]
buckets = [0]*(max(nums)-min(nums)+1) #最大数和最小数之间,一个桶里放一个数
# 遍历数组,下标对应数字,数组内容对应频数
for i in nums:
buckets[i-min(nums)]+=1
print(buckets)
#遍历桶,根据频数输出数字(根据数组内容输出下标的次数)
for i in range(len(buckets)):
if buckets[i]:
res.extend([i+min(nums)]* buckets[i])
res
output
[2, 3, 1, 0, 0, 0, 2]
[2, 2, 3, 3, 3, 4, 8, 8]
关键点是 min(nums) 扮演的作用和地位,以及合并列表用的是 extend 不是 append
显然,当数字跨度较大,用下标表示数字,数组内容表示对应数字频数的时候并不合适,因此,我们换一下,用下标表示频数,数组内容表示该频数的数字,此时同一频数的数字可能有多种,所以要构建二维数组,行表示频数,列表示该频数的数字!
class Solution(object):
def topKFrequent(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
dict1 = {} # keys 数字,values 频数
res = []
for i in nums:
if i in dict1:
dict1[i]+=1
else:
dict1[i]=1
buckets=[[] for i in range(len(nums)+1)] # [[],[],...[]],加一多了个频数0
for key in dict1:# 这里表示遍历字典 key,也即数字
buckets[dict1[key]].append(key) #将数字存放在对应的频数下标中
for i in range(len(nums),-1,-1): #从后往前扫描,第一个-1是为了兼顾0下标,第二个-1表示倒序,len(nums)因为 buckets长度是 len(nums)+1
if buckets[i]: # 如果对应频数有数字
for j in buckets[i]: # 遍历该频数的所有数字
if len(res)==k: # 按题目要求输出频数最高的K个
break
else:
res.append(j) #搜集符合条件的数字
return res
eg:
nums = [2,8,3,2,3,8,3,4]
k = 2
- dict1 为 {2: 2, 8: 2, 3: 3, 4: 1} 表示 2 出现 2 次,8 出现 2 次,3 出现 3 次,4 出现 1 次
- 初始化的 buckets 为 [[], [], [], [], [], [], [], [], []]
- 装入信息的 buckets [[], [4], [2, 8], [3], [], [], [], [], []] 表示 4 出现 1 次,2,8 出现 2 次,3 出现 3 次
- 输出结果 [3, 2]
378. 有序矩阵中第K小的元素(排序)
给定一个 n x n 矩阵,其中每行和每列元素均按升序排序,找到矩阵中第k小的元素。
请注意,它是排序后的第k小元素,而不是第k个元素。
-
示例:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
返回 13。 -
说明:
你可以假设 k 的值永远是有效的, 1 ≤ k ≤ n2 。
思路,将二维 matrix 拉成一维的,用 list 的 extend 功能,然后排序(这个可以自由发挥,我用的 sorted),返回 list[k-1]
class Solution(object):
def kthSmallest(self, matrix, k):
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
sort_list = []
for i in range(len(matrix)):
sort_list.extend(matrix[i])
sort_list = sorted(sort_list)
return sort_list[k-1]
不过这样没有充分利用数组的有序信息,还可以用二分查找来算……(bryant)
1051. 高度检查器(排序)
学校在拍年度纪念照时,一般要求学生按照 非递减 的高度顺序排列。
请你返回至少有多少个学生没有站在正确位置数量。该人数指的是:能让所有学生以 非递减 高度排列的必要移动人数。
-
示例:
输入:[1,1,4,2,1,3]
输出:3
解释:
高度为 4、3 和最后一个 1 的学生,没有站在正确的位置。 -
提示:
1 <= heights.length <= 100
1 <= heights[i] <= 100
一开始比比划划,束手无策,找不到很好的泛化方式,升序排序后,比较排序后和排序前的差异就可以得出结果了!这里我用的是快排!
class Solution(object):
def heightChecker(self, heights):
"""
:type heights: List[int]
:rtype: int
"""
original_heights = [] # 不先定义会报错
original_heights[:] = heights[:]#deep copy,因为快排会改变list
# 快排
def quick_sort(num,start,end):
if start<end:
base = split(num,start,end)
quick_sort(num,start,base-1)
quick_sort(num,base+1,end)
return num
def split(nums,start,end):
l = start
r = end
base = nums[l]
while(l<r):
while l<r and nums[r]>=base:
r-=1
nums[l] = nums[r]
while l<r and nums[l]<=base:
l+=1
nums[r] = nums[l]
nums[l] = base
return l
sorted_heights = quick_sort(heights,0,len(heights)-1)
num = 0 # 记录不一样的数字
for i in range(len(heights)):
if original_heights[i]!= sorted_heights[i]:
num+=1
return num
17. 电话号码的字母组合(递归)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

- 示例:
输入:“23”
输出:[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
思路:字符串长度为 n n n,便利第一个字符串和 1 :n 的字符串结合,递归下去,如果字符串长度为1,返回数字对应的字母!
class Solution(object):
def letterCombinations(self, digits):
"""
:type digits: str
:rtype: List[str]
"""
dict_nums = {
2:['a','b','c'],
3:['d','e','f'],
4:['g','h','i'],
5:['j','k','l'],
6:['m','n','o'],
7:['p','q','r','s'],
8:['t','u','v'],
9:['w','x','y','z']
}
if digits == "":
return []
if len(digits) == 1:
return dict_nums[int(digits)]
dict_nums_next = self.letterCombinations(digits[1:])
result = []
for i in dict_nums[int(digits[0])]:
for j in dict_nums_next:
result.append(i+j)
return result
241. 为运算表达式设计优先级(分治)
给定一个含有数字和运算符的字符串,为表达式添加括号,改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。
-
示例 1:
输入: “2-1-1”
输出: [0, 2] -
解释:
( ( 2 − 1 ) − 1 ) = 0 ((2-1)-1) = 0 ((2−1)−1)=0
( 2 − ( 1 − 1 ) ) = 2 (2-(1-1)) = 2 (2−(1−1))=2 -
示例 2:
输入: " 2 ∗ 3 − 4 ∗ 5 " "2*3-4*5" "2∗3−4∗5"
输出: [ − 34 , − 14 , − 10 , − 10 , 10 ] [-34, -14, -10, -10, 10] [−34,−14,−10,−10,10] -
解释:
( 2 ∗ ( 3 − ( 4 ∗ 5 ) ) ) = − 34 (2*(3-(4*5))) = -34 (2∗(3−(4∗5)))=−34
( ( 2 ∗ 3 ) − ( 4 ∗ 5 ) ) = − 14 ((2*3)-(4*5)) = -14 ((2∗3)−(4∗5))=−14
( ( 2 ∗ ( 3 − 4 ) ) ∗ 5 ) = − 10 ((2*(3-4))*5) = -10 ((2∗(3−4))∗5)=−10
( 2 ∗ ( ( 3 − 4 ) ∗ 5 ) ) = − 10 (2*((3-4)*5)) = -10 (2∗((3−4)∗5))=−10
( ( ( 2 ∗ 3 ) − 4 ) ∗ 5 ) = 10 (((2*3)-4)*5) = 10 (((2∗3)−4)∗5)=10
这个题目也有点分治的意思,但是主体还是递归,思路如下(参考 LeetCode - 241. Different Ways to Add Parentheses(分治、dp) ):
- 递归函数,遍历当前字符串,只要有符号是
+、-、*的就将整个字符串分开成两半; - 然后左边一半的字符串去递归求出那个解的集合,右边的也求出解的集合;
- 最后关键的是当前的字符串的解是左和右的
笛卡尔积(这个操作尤为重要);

图片来源 https://blog.csdn.net/zxzxzx0119/article/details/83748086
class Solution(object):
def diffWaysToCompute(self, input):
"""
:type input: str
:rtype: List[int]
"""
# 递归终止条件,全部是数字
if input.isdigit():
return [int(input)]
res = []
for i in range(len(input)):
if input[i] in "+-*":
L = self.diffWaysToCompute(input[:i]) # 记得 self
R = self.diffWaysToCompute(input[i+1:])
# 遍历左右 str,计算笛卡尔积
for l in L:
for r in R:
if input[i] == "+":
res.append(l+r)
elif input[i] == "-":
res.append(l-r)
else:
res.append(l*r)
return res # 记得返回,不然 return None 会报错 TypeError: 'NoneType' object is not iterable"
455. 分发饼干(贪心)
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。对每个孩子 i ,都有一个胃口值 gi ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j ,都有一个尺寸 sj 。如果 sj >= gi ,我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
-
注意:
你可以假设胃口值为正。
一个小朋友最多只能拥有一块饼干。 -
示例 1:
输入: [1,2,3], [1,1]
输出: 1 -
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。 -
示例 2:
输入: [1,2], [1,2,3]
输出: 2 -
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
参考 LeetCode-Python-455. 分发饼干
孩子需求从小到大排序,饼干从小到大发放
满足孩子需求的话,有请下一位小朋友和下一个饼干,结果统计加1
不然就换个更大的饼干来满足当前的小朋友
直到饼干发完或者小朋友都被满足
class Solution(object):
def findContentChildren(self, g, s):
"""
:type g: List[int]
:type s: List[int]
:rtype: int
"""
g = sorted(g)
s = sorted(s)
child = 0
cake = 0
while(child<len(g) and cake<len(s)):
if g[child]<=s[cake]:
child+=1 # 得到了满足就有请下一位
cake+=1 # 从小到大发饼干
return child # 返回被满足的孩子数量