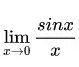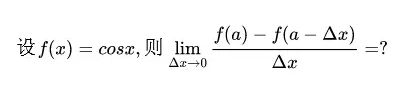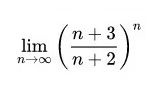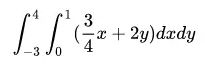【python】sympy
文章目录
- 1 simplify 表达式化简
- 2 expand 表达式展开
- 3 solve 方程自动求解
- 4 limit 求极限
- 5 diff 求导
- 6 dsolve 计算微分方程
- 7 intergrate 积分计算
- 7.1 定积分
- 7.2 不定积分
- 7.3 二重积分
- 7.4 二重不定积分
Sympy是一个数学符号库(sym代表了symbol,符号),包括了积分,微分方程等各种数学运算方法,为python提供了强大的数学运算支持。对于图像来说,虽然都是做离散的计算,操作最多的还是numpy里的数组,但实际上,这个库包含了积分微分,三角等最基本的数学运算,可以说是工科最基本的,用起来媲美matlab。1
感受一下魅力
import sympy,math
import numpy as np
print(math.sqrt(2)**2)
print(np.sqrt(2)**2)
print(sympy.sqrt(2)**2)
1 simplify 表达式化简
from sympy import *
x,y,z,a,b,c = symbols('x,y,z,a,b,c')
f = (2/3)*x**2 + (1/3)*x**2 + x + x + 1
#simplify(f)
f.simplify()
output
1.0*x**2 + 2*x + 1
2 expand 表达式展开
f = (x+1)**2
expand(f)
#f.expand()
output
x**2 + 2*x + 1
3 solve 方程自动求解
f1 = 2*x - y + z - 10
f2 = 3*x + 2*y - z - 16
f3 = x + 6*y - z - 28
solve([f1,f2,f3])
output
{x: 46/11, y: 56/11, z: 74/11}
4 limit 求极限
首先,limit可以作为普通的带入化简求值方法。
f = (x+1)**2 + 1
limit(f,x,a-1)
output
a**2 + 1
f = (x+1)**2 + 1
limit(f,x,1)
output
5
f = sin(x)/x
limit(f,x,0)
output
1
#从负方向逼近,dir可以取'+' 或者 '-'
limit(f,x,0,dir='-')
output
1
dx = symbols('dx')
f = cos(x)
f1 = (limit(f,x,a)-limit(f,x,a-dx))/dx
limit(f1,dx,0)
output
-sin(a)
f = ((x+3)/(x+2))**x
print(limit(f,x,oo))
print(float(E))
print(type(E))
output
E
2.718281828459045
<class 'sympy.core.numbers.Exp1'>
5 diff 求导
diff(你的函数,自变量,求导的次数),默认1次
print(diff(sin(2*x),x,1))
print(sin(2*x).diff(x))
print(diff(sin(2*x),x))
print(diff(sin(x*y),x,1,y,1)) # 先对x求一次导,再对y求一次倒
output
2*cos(2*x)
2*cos(2*x)
2*cos(2*x)
-x*y*sin(x*y) + cos(x*y)
6 dsolve 计算微分方程
f = symbols("f")
x = symbols("x", real=True) # 定义符号x 为实数
eq1 = dsolve(f(x).diff(x)+f(x)**2+f(x),f(x))
eq1
output
Eq(f(x), -C1/(C1 - exp(x)))
如果设置hint参数为“best”,就能得到更简单的显函数表达式
eq2 = dsolve(f(x).diff(x) + f(x)**2 + f(x), f(x), hint="best")
eq2
output
Eq(f(x), -C1/(C1 - exp(x)))
7 intergrate 积分计算
7.1 定积分
integrate(exp(x),(x,-oo,0))
output
1
7.2 不定积分
f = 3*x**2 + 1
integrate(f,x)
output
x**3 + x
7.3 二重积分
f = (3/4)*x + 2*y
integrate(f,(x,0,1),(y,-3,4))
output
9.62500000000000
7.4 二重不定积分
f = (3/4)*x + 2*y
integrate(f,(x,0,1),(y,-x,x))
output
0.75*x
用Python解决高数所有计算题–sympy求解极限、积分、微分、二元一次方程等 ↩︎