7.机器学习sklearn-------线性回归（房价与房屋尺寸关系的线性拟合）

1.基本概念

线性回归(Linear Regression)是利用数理统计中回归分析， 来确定两种或两种以上变量间相互依赖的定量关系的一种统计分 析方法。 

线性回归利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模。这种函数是一个或多个称为回 归系数的模型参数的线性组合。只有一个自变量的情况称为简单 回归,大于一个自变量情况的叫做多元回归。

2.用途

线性回归有很多实际的用途，分为以下两类： 

1.如果目标是预测或者映射，线性回归可以用来对观测数据集的y和X的值拟合出一个预测模型。当完成这样一个模型以后，对于一个新增的X值， 在没有给定与它相配对的y的情况下，可以用这个拟合过的模型预测出一个 y值。

2..给定一个变量y和一些变量X1,⋯,Xp,这些变量有可能与y相关，线 性回归分析可以用来量化y与Xj之间相关性的强度，评估出与y不相关的Xj， 并识别出哪些Xj的子集包含了关于y的冗余信息。

3.实例

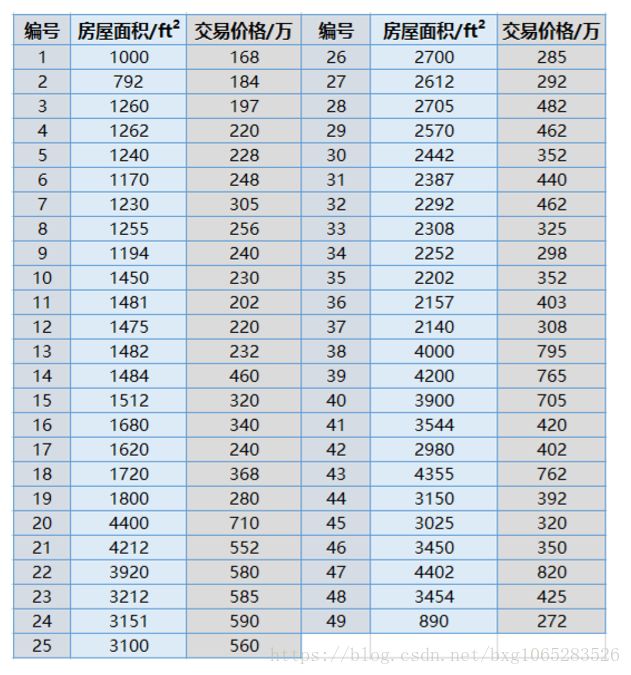
与房价密切相关的除了单位的房价，还有房屋的尺寸。我们可以根 据已知的房屋成交价和房屋的尺寸进行线性回归，继而可以对已知房屋尺 寸，而未知房屋成交价格的实例进行成交价格的预测。

目标：对房屋成交信息建立回归方程，并依据回归方程对房屋价格进行预测 

4.数据

为了方便展示，成交信息只使用 了房屋的面积以及对应的成交价格。 其中： 

• 房屋面积单位为平方英尺（ft2）

• 房屋成交价格单位为万

                             

5.可行性分析

• 简单而直观的方式是通过数据的可视化直接观察房屋成交价格与房 屋尺寸间是否存在线性关系。

• 对于本实验的数据来说，散点图就可以很好的将其在二维平面中进 行可视化表示。

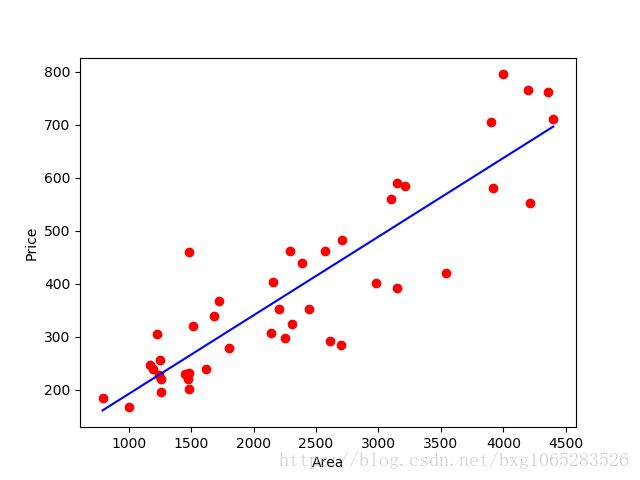
下图为数据的散点图，其中横坐标为房屋面积，纵坐标为房屋的成 交价格。可以看出，靠近坐标左下 角部分的点，表示房屋尺寸较小的 房子，其对应的房屋成交价格也相 对较低。同样的，靠近坐标右上部 分的点对应于大尺寸高价格的房 屋。从总体来看，房屋的面积和成 交价格基本成正比。

6.实验过程

使用算法：线性回归 

实现步骤： 1.建立工程并导入sklearn包 

                  2.加载训练数据，建立回归方程

                  3.可视化处理

调用sklearn.linear_model.LinearRegression()所需参数：

 • fit_intercept : 布尔型参数，表示是否计算该模型截距。可选参数。

 • normalize : 布尔型参数，若为True，则X在回归前进行归一化。可选参数。默认值为False。

 • copy_X : 布尔型参数，若为True，则X将被复制；否则将被覆盖。可选参数。默认值为True。

 • n_jobs : 整型参数，表示用于计算的作业数量；若为-1，则用所有的CPU。可选参数。默认值为1。

线性回归fit函数用于拟合输入输出数据，调用形式为linear.fit(X,y, sample_weight=None)：

 • X : X为训练向量；

 • y : y为相对于X的目标向量； 

 • sample_weight : 分配给各个样本的权重数组，一般不需要使用，可省略。

#表示matplotlib的pyplot子库，它提供了和matlab类似的绘图API
import  matplotlib.pyplot as plt
#表示可以调用sklearn中的 linear_model模块进行线性回归。
from sklearn import  linear_model
import numpy as np
#建立datasets_X和datasets_Y用来存储数据中的房屋尺寸和房屋成交价格。
datasets_X =[]
datasets_Y =[]
fr =open('prices.txt','r')
#一次读取整个文件。
lines =fr.readlines()
#逐行进行操作，循环遍历所有数据
for line in lines:
    #去除数据文件中的逗号
    items =line.strip().split(',')
    #将读取的数据转换为int型，并分别写入datasets_X和datasets_Y。
    datasets_X.append(int(items[0]))
    datasets_Y.append(int(items[1]))
#求得datasets_X的长度，即为数据的总数。
length =len(datasets_X)
#将datasets_X转化为数组， 并变为二维，以符合线性回 归拟合函数输入参数要求
datasets_X= np.array(datasets_X).reshape([length,1])
#将datasets_Y转化为数组
datasets_Y=np.array(datasets_Y)

minX =min(datasets_X)
maxX =max(datasets_X)
#以数据datasets_X的最大值和最小值为范围，建立等差数列，方便后续画图。
X=np.arange(minX,maxX).reshape([-1,1])

linear =linear_model.LinearRegression()
linear.fit(datasets_X,datasets_Y)#调用线性回归模块，建立回归方程，拟合数据
#查看回归方程系数
print('Cofficients:',linear.coef_)
#查看回归方程截距
print('intercept',linear.intercept_)

#3.可视化处理
#scatter函数用于绘制数据 点，这里表示用红色绘制数据点；
plt.scatter(datasets_X,datasets_Y,color='red')
#plot函数用来绘制直线，这 里表示用蓝色绘制回归线；
#xlabel和ylabel用来指定横纵坐标的名称
plt.plot(X,linear.predict(X),color='blue')
plt.xlabel('Area')
plt.ylabel('Price')
plt.show()

运行结果：

Cofficients: [0.14839484]
intercept 43.92337096187816

通过回归方程拟合的直线与原 有数据点的关系如下图所示，依据该回归方程即可通过房屋的尺寸， 来预测房屋的成交价格。