关于解决Hash冲突的线性探测开放地址法和拉链法
在实际应用中,无论如何构造哈希函数,冲突是无法完全避免的。
开放地址法
这个方法的基本思想是:当发生地址冲突时,按照某种方法继续探测哈希表中的其他存储单元,直到找到空位置为止。这个过程可用下式描述:
H i ( key ) = ( H ( key )+ d i ) mod m ( i = 1,2,…… , k ( k ≤ m – 1))
其中: H ( key ) 为关键字 key 的直接哈希地址, m 为哈希表的长度, di 为每次再探测时的地址增量。
采用这种方法时,首先计算出元素的直接哈希地址 H ( key ) ,如果该存储单元已被其他元素占用,则继续查看地址为 H ( key ) + d 2 的存储单元,如此重复直至找到某个存储单元为空时,将关键字为 key 的数据元素存放到该单元。
增量 d 可以有不同的取法,并根据其取法有不同的称呼:
( 1 ) d i = 1 , 2 , 3 , …… 线性探测再散列;
( 2 ) d i = 1^2 ,- 1^2 , 2^2 ,- 2^2 , k^2, -k^2…… 二次探测再散列;
( 3 ) d i = 伪随机序列 伪随机再散列;
例1设有哈希函数 H ( key ) = key mod 7 ,哈希表的地址空间为 0 ~ 6 ,对关键字序列( 32 , 13 , 49 , 55 , 22 , 38 , 21 )按线性探测再散列和二次探测再散列的方法分别构造哈希表。
解:
( 1 )线性探测再散列:
32 % 7 = 4 ; 13 % 7 = 6 ; 49 % 7 = 0 ;
55 % 7 = 6 发生冲突,下一个存储地址( 6 + 1 )% 7 = 0 ,仍然发生冲突,再下一个存储地址:( 6 + 2 )% 7 = 1 未发生冲突,可以存入。
22 % 7 = 1 发生冲突,下一个存储地址是:( 1 + 1 )% 7 = 2 未发生冲突;
38 % 7 = 3 ;
21 % 7 = 0 发生冲突,按照上面方法继续探测直至空间 5 ,不发生冲突,所得到的哈希表对应存储位置:
下标: 0 1 2 3 4 5 6
49 55 22 38 32 21 13
( 2 )二次探测再散列:
下标: 0 1 2 3 4 5 6
49 22 21 38 32 55 13
注意:对于利用开放地址法处理冲突所产生的哈希表中删除一个元素时需要谨慎,不能直接地删除,因为这样将会截断其他具有相同哈希地址的元素的查找地址,所以,通常采用设定一个特殊的标志以示该元素已被删除。
例子
已知一个线性表(38,25,74,63,52,48),假定采用h(k)=k%6计算散列地址进行散列存储,若用线性探测的开放定址法处理冲突,则在该散列表上进行查找的平均查找长度为()。
A. 1.5 B. 1.7 C. 2 D. 2.3 2、
解题过程:
(1)计算h(k): 38%6 = 2 25%6 = 1 74%6 = 2 63%6 = 3 52%6 = 4 48%6 = 0
(2)定址: 把不冲突的和冲突的全部列出来即可 地址: 0 1 2 3 4 5
1、线性表第1个元素(38): 38(第1 次不冲突)
2、线性表第2个元素(25): 25(第1次不冲突)
3、线性表第3个元素(74): 74(第1 次冲突,地址 + 1)
4、线性表第3个元素(74): 74(第2 次不冲突)
5、线性表第4个元素(63): 63(第1 次冲突,地址 + 1)
6、线性表第4个元素(63): 63(第2 次不冲突)
7、线性表第5个元素(52): 52(第1 次冲突,地址 + 1)
8、线性表第5个元素(52): 52(第2 次不冲突)
9、线性表第6个元素(48): 48(第1次不冲突)
经过上述定址过程,线性表中的各个元素都有了唯一的地址。
2.3、结果 线性表中的 6 个元素,经过9次定址, 在该散列表上进行查找的平均查找长度为:9/6 = 1.5, 答案选:A
三、哈希表查找不成功怎么计算?
解答:先建好表,然后可以算出每个位置不成功时的比较次数之和,再除以表空间个数!
例如:散列函数为hash(x)=x MOD 13,用线性探测,建立了哈希表之后,如何求查找不成功时的平均查找长度!?
地址: 0 1 2 3 4 5 6 7 8 9 10 11 12
数据: 39 12 28 15 42 44 6 25 - - 36 - 38
成功次数: 1 3 1 2 2 1 1 9 1 1
不成功次数: 9 8 7 6 5 4 3 2 1 1 2 1 10
查找成功时的平均查找长度:ASL=(1+3+1+2+2+1+1+9+1+1)/10 =2.2
查找不成功时的平均查找长度:ASL=(9+8+7+6+5+4+3+2+1+1+2+1+10)/13=4.54
链地址法
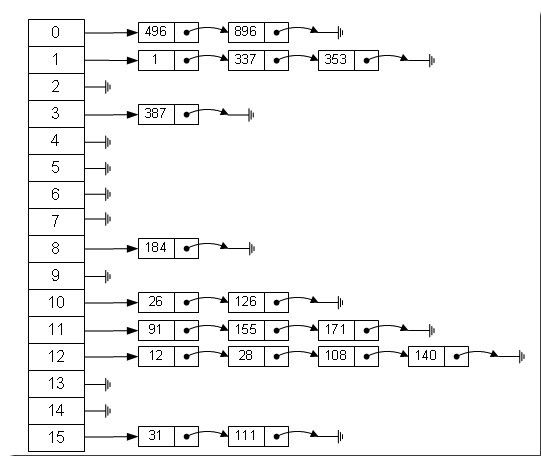
链地址法解决冲突的做法是:如果哈希表空间为 0 ~ m - 1 ,设置一个由 m 个指针分量组成的一维数组 ST[ m ], 凡哈希地址为 i 的数据元素都插入到头指针为 ST[ i ] 的链表中。这种方法有点近似于邻接表的基本思想,且这种方法适合于冲突比较严重的情况。
链地址法解决冲突的哈希表如下图所示。
哈希特点:
通过散列算法,变换成固定长度的输出;
散列值的空间通常远小于输入的空间, 不同的输入可能会散列成相同的输出,
而不可能从散列值来唯一的确定输入值
一种将任意长度的消息压缩到某一固定长度的消息摘要的函数 HASH主要用于
信息安全领域中加密算法,一些不同长度的信息转化成杂乱的128位的编码,HASH值
哈希表长度该定义多大:
一般采用哈希算法的时候,哈希表的长度设为多大?有什么依据?
越长碰撞越少,但耗得资源也就多了
最大的出发点就是没有冲突
哈希就是散列,散列就是把关键字分布均匀撒到到每一个桶内,哈希表越长,散列函数越好,自然查找效率就越高.
哈希表长度定义举例说明:
比如说要处理的数据集合有100,000个,每一项的数据占用内存约为50bytes,我的哈希表的长度在多大比较合适?
hash表里面存指针,表长整成数据集合的10倍,100000*4*10 也就是4MB内存
空间换时间(越长碰撞越少,内存消耗越多,查找和插入速率越接近O(1))
一万,一千万,一亿数据需要多少空间:
1万数据,1个数据1Byte
1,0000 -> 10,000 大约10KB
1千万数据,1个数据1Byte
1000,0000 -> 10,000,000 大约10M
1亿数据,1个数据1Byte
10000,0000 -> 100,000,000 大约100M
10亿数据,1个数据1Byte
10,0000,0000 -> 1,000,000,000 大约1G
1Byte = 8bit 表示最大数值 2^8 = 256
2Byte = 2*8bit 表示最大数值 2^16 = 65536 = 6,5536(约6千) = 65,536
4Byte = 4*8bit 表示最大数值 2^32 = 4294967296 = 42,9496,7296(约42亿) = 4,294,967,296
32位机器,地址4个字节表示,寻址就是42,9496,7296(约42亿),所以内存最多可以用4G,但不是所有地址都用于内存,所以内存最大支持会小于4G。
部分转载自:https://blog.csdn.net/noble_happy/article/details/78934294
https://blog.csdn.net/w_fenghui/article/details/2010387