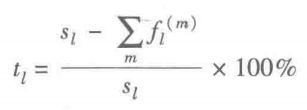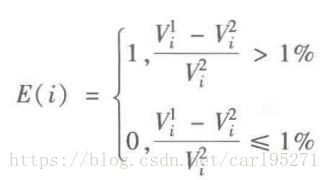数据挖掘项目---电力窃漏电用户自动识别
1.挖掘目标
1) 归纳出窃漏电用户的关键特征,构建窃漏电用户的识别模型
2) 利用实时监测数据,调用窃漏电用户识别模型,实现实时诊断
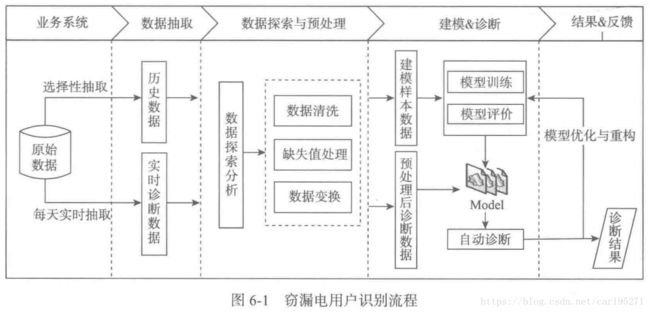
2.分析方法与过程
1) 从电力计量自动化系统、营销系统有选择性的抽取部分大用户用电负荷、终端报警及违约窃电处罚信息等原始数据。
2) 对样本数据探索分析,剔除不可能存在窃漏电行为行业的用户,即白名单用户,初步审视正常用户和窃漏电用户的用电特征。
3) 对样本数据进行预处理,包括数据清洗、缺失值处理和数据变换。
4) 构建专家样本集。
5)构建漏电用户识别模型。
6) 在线监测用户用电负荷及终端报警,调用模型实现实时诊断。
2.1 数据抽取
主要是获取和窃漏电相关的原始数据(随书也没有提供这方面的原始数据)。相关的原始数据主要有用电负荷数据、终端报警数据、违约窃电处罚信息以及用户档案资料等。
2.2 数据探索分析
主要是对数据进行初步的研究,发现数据的内在规律特征,有助于选择合适的数据预处理和数据分析技术。本案例主要采用分布分析和周期性分析等方法对电量数据进行数据探索分析。
1.分布分析
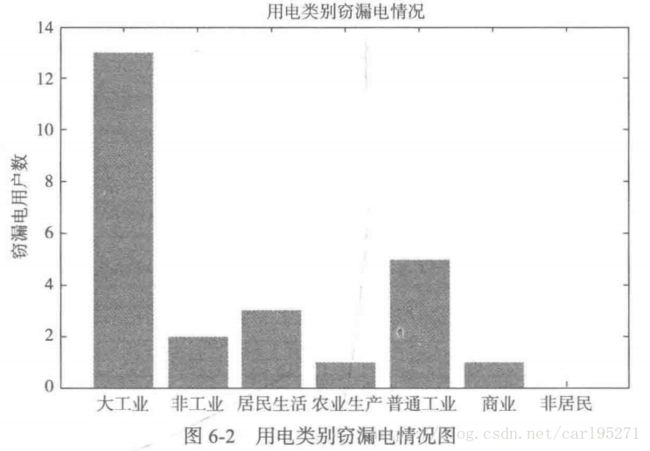
对2009年1月1日至2014年12月31日共5年所有的窃漏电用户进行分布分析,统计出各个类别用户的窃漏电用户分布情况,从下图中可以发现非居民类别不存在窃漏电情况,故在后面的数据预处理环节中,不考虑非居民类别的用电数据。
2.周期性分析
随机抽取一个正常用电用户和一个窃电用户,采用周期性分析对用电量进行探索。
(1)正常用户用电电量探索分析
下图是一个月内,正常用户每一天的用电量的分布状况。总体来看该用户用量比较稳定,没有太大的波动,这就是用户正常用电的电量指标特征。
(2) 窃漏电用户用电量探索分析
可以明显得看到,窃漏电用户的用电量出现了明显的下降趋势,该用户从2014年9月1号开始用电量下降,并且持续下降,这就是用户异常用电的电量指标特征。
2.3 数据预处理
1.数据清洗
1)由前面的数据探索得知,需要将非居民用电类别的用电数据过滤掉。
2)节假日的用电量会比工作日的明显偏低,为了尽可能达到较好的数据效果,过滤节假日的用电数据。
2.缺失值处理
存在有一些用户在某一天的用电量数据缺失了(...\chapter6\demo\data\missing_data.xls)。若将这些值抛弃掉,会严重影响供出电量的计算结果,最终导致日线损率数据误差很大。为了达到较好的数据效果,需要对缺失值处理。这里采用拉格朗日插值法对缺失值进行插值。
拉格朗日插值法具体的思路为:首先从原始数据集中确定因变量和自变量,取出缺失值前后各5个数据(前后数据中遇到数据不存在或者为空的,直接将数据社区,将仅有的数据组成一组),然后用一个高次多项式去拟合这10个数据,求出拟合曲线,用拟合曲线去预测缺失数据。具体代码和注释如下:
#-*- coding:utf-8 -*-
import pandas as pd
from scipy.interpolate import lagrange #interpolate是scipy的一个子库,包含大量的插值函数
inputfile = 'D:/Python DS DM/chapter6/demo/data/missing_data.xls' #输入数据路径,具体路径得修改
outputfile = 'D:/Python DS DM/practice code/chp06/tmp/missing_data_processed.xls' #输出数据路径
data = pd.read_excel(inputfile,header=None) #读入,header=None 没有表头
#自定义列向量插值函数
#s为列向量(Series),n为被插值的位置,k为取前后的数据个数,默认为5
def polyinterp_column(s,n,k=5):
y = s[list(range(n-k,n)) + list(range(n+1,n+1+k))]
#将s列向量中,n位置处,前k个和后k个数取出组成一个新的Series列向量
y=y[y.notnull()] #剔除空值,y中可能不到2k个数
#y.notnull() 也是一个布尔值的series列向量
return lagrange(y.index,list(y))(n)
#y.index 自变量。list(y) 因变量
#lagrange(y.index,list(y))应该是一个拟合好的插值函数,再f(n)
#逐个元素判断是否需要插值
for i in data.columns: #所有列
for j in range(len(data)): #len(DataFrame) 是行的数目
if (data[i].isnull())[j]: #data[i].isnull()是一个series的布尔列向量
(data[i])[j] = polyinterp_column(data[i],j)
data.to_excel(outputfile,header=None,index=False) #去掉行列索引输出3.数据变换
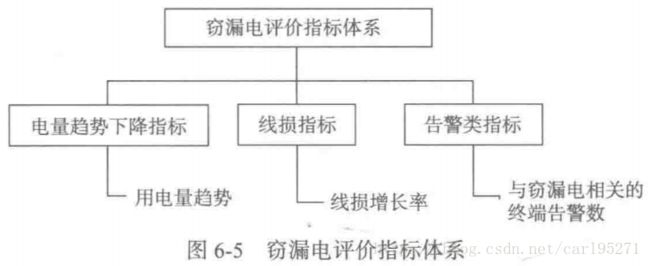
数据变换的目的:通过电力计量系统采集的电量、负荷,虽然在一定程度上能反映用户窃漏电行为的某些规律,但要作为构建模型的专家样本,特征不明显。基于数据变换,得到新的评价指标来表征窃漏电行为所具有的规律,评价指标体系如下图:
(1)电量趋势下降指标
统计某一天的电量下降趋势指标时,可以设定这一天前后各5天为统计的区间,计算这11天内的电量变化趋势。首先计算这11天的每天的电量变化趋势,其中第i天的电量变化趋势是考虑前后5天期间的用电量斜率,用最小二乘法得到这第i天前后5天,共11天的斜率:
若用电量趋势是不断下降的,则认为具有一定的窃电嫌疑。故计算这11天以内,当天比前一天用电量趋势减少的总天数:
(2)线损指标
线损率用于衡量供电线路的损失比例,一条线路上同时供给多个用户,若第l天的线路供电量为Sl,线路上各个用户的总用电量为 ,则线路线损率计算公式如下:
,则线路线损率计算公式如下:
对统计当天设定前后5天为统计窗口期,首先分别统计当天与前5天之间的线损率平均值![]() ,统计当天与后5天之间的线损率平均值
,统计当天与后5天之间的线损率平均值![]() ,若
,若![]() 比
比![]() 的增长率大于1%,则认为有一定的窃电嫌疑,故定义线损率指标如下:
的增长率大于1%,则认为有一定的窃电嫌疑,故定义线损率指标如下:
(3)告警类指标
与窃漏电相关的终端报警主要有电压缺相、电压断相、电流反极性等告警,计算发生与窃漏电相关的终端报警的次数总和,作为告警类指标。
2.4 构建专家样本
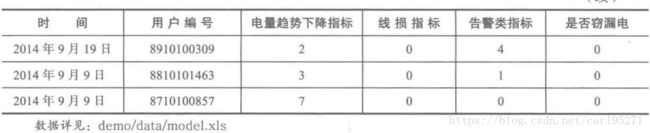
对2009年1月1日至2014年12月31日所有窃漏电用户及正常用户的电量、告警及线损数据和该用户在当天是否窃漏电的标识,按窃漏电评价指标进行处理并选取其中291个样本数据,得到专家样本库,数据详见 'demo/data/model.xls'
2.5 模型构建
1.构建窃漏电用户识别模型
在专家样本准备完成后,需要划分测试样本和训练样本,随机选取20%作为测试样本,剩下的作为训练样本。采用CART决策树分类模型来构建分类模型。构建CART决策树模型时输入项包括电量趋势下降指标、线损类指标和告警类指标,输出项为窃漏电标识。
(1)数据划分
对专家样本随机选取20%作为测试样本,剩下的80%作为训练样本。
#-*- coding: utf-8 -*-
import pandas as pd
from random import shuffle #导入随机函数shuffle,用来打乱数据,random是python内置模块
datafile = 'D:/Python DS DM/chapter6/demo/data/model.xls'
data = pd.read_excel(datafile)
data = data.as_matrix() #Convert the frame to its Numpy-array representation.
shuffle(data) #随机打乱数据
p=0.8 #设置训练数据比例
#len(DataFrame) or len(array) 返回行的数目
train = data[:int(len(data)*p),:] #前80%作为训练集
test = data[int(len(data)*p):,:] #后20%作为测试集(2)CART决策树
通过Scikit-Learn利用训练样本构建CART决策树模型,具体代码及注释如下:
#构建CART决策树模型
from sklearn.tree import DecisionTreeClassifier #导入决策树模型
treefile = 'D:/Python DS DM/practice code/chp06/tmp/tree.pk1' #模型输出名字
tree = DecisionTreeClassifier() #建立决策树模型
tree.fit(train[:,:3],train[:,3]) #训练模型
#保存模型
from sklearn.externals import joblib
joblib.dump(tree,treefile)
from cm_plot import * #导入自行编写的混淆矩阵可视化函数
cm_plot(train[:,3],tree.predict(train[:,:3])).show() #显示混淆矩阵可视化结果,cm_plot()函数返回plt,故能直接调用show()方法
#tree.predict() 函数直接给出预测结果,返回一个arraydef cm_plot(y, yp):
from sklearn.metrics import confusion_matrix #导入混淆矩阵函数
cm = confusion_matrix(y, yp) #混淆矩阵
import matplotlib.pyplot as plt #导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图,配色风格使用cm.Greens,更多风格请参考官网。
plt.colorbar() #颜色标签
for x in range(len(cm)): #数据标签
for y in range(len(cm)):
plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label') #坐标轴标签
plt.xlabel('Predicted label') #坐标轴标签
return plt混淆矩阵给出了预测结果的评价状况:
1)分类准确率(Accurancy)(160+56)/(160+56+3+13)=93.1%
2)正常用户被误判为窃漏电用户占正常用户的 13/(13+160)=7.5% (FP/(FP+TN) 1是正例Positive,0是负例Negative
3)窃漏电用户被误判为正常用户占正常窃漏电用户的3/(3+56)=5.1% (FN/(FN+TP))
2.模型评价
为了进一步评估模型的分类性能,故菜用测试样本对模型进行评价,采用ROC曲线评价方法进行评估,一个优秀的分类器所对应的ROC曲线应该是尽量靠近左上角的。CART决策树对测试数据集的测试代码如下所示:
from sklearn.metrics import roc_curve #导入ROC曲线函数
fpr, tpr, thresholds = roc_curve(test[:,3], tree.predict_proba(test[:,:3])[:,1], pos_label=1)
#tpr:true positive rate 真阳率,TPR=TP/(TP+FN) 所有真实正例样本中被预测正确的比例
#fpr:false positive rate 假阳率,FPR=FP/(TN+FP) 所有真实负例样本中被预测为正例的比例
#thresholds: 关于阈值截断点的含义参考下这个博客:https://blog.csdn.net/ybdesire/article/details/51999995
# https://blog.csdn.net/hh1294212648/article/details/77649127
#test[:,3] : y_true 真实的二元标签,array结构的
#tree.predict_proba()返回一个2d-array,第1列是负类的概率,第2列是正类的概率,区别tree.predict()
#pos_label=1: 正例标签是1
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of CART', color = 'green') #作出ROC曲线
plt.xlabel('False Positive Rate') #坐标轴标签
plt.ylabel('True Positive Rate') #坐标轴标签
plt.ylim(0,1.05) #边界范围
plt.xlim(0,1.05) #边界范围
plt.legend(loc=4) #图例,loc=4对应lower right的位置放置图例
plt.show() #显示作图结果