noip2010提高组
最近几次始终考的不怎么好，思路比较死。
---------------------------------------------------------------------------------------------------------------------------
一道简单的模拟，不多说，用stl很简单直观
代码：
#include
#include
#include
#include
#include
#include
#include
#include 
很明显的动规题，一开始想到的状态是：f[i]代表当走到第i个格子时的最大分数。
但后来分析一下题意发现卡片的消耗导致这种状态不能完成此题（因为这么定义无法判定卡片怎么消耗）
想了很久没想到，只好打了个深搜暴力放着。
考后看到std才知道原来状态是围绕卡片定义的：f[i][j][k][l]代表用了i张1步，j张2步，k张3步，l张4步。
而当前格数就用r = 1（一开始就在第一格） + i + j*2 + k*3 + l*4 算出来的！
想来是个不难的简单动规，可惜想到的人寥寥无几。
代码如上所述：
#include
using namespace std;
#define RG register
#define ll long long
#define in(x) x = read()
#define lin(x) scanf("%lld",&x)
#define llin(x) x = lread
#define din(x) scanf("%lf",&x)
#define dout(x) printf("%lf",x)
#define out(x) print(x)
#define lout(x) printf("%lld",x)
#define ex putchar('\n')
#define ko putchar(' ')
const ll p = 1e10 + 7;
const int MAXN = 351;
int n,m;
int w[MAXN];
int f[41][41][41][41];
int v[MAXN];
inline int read()
{
int X=0,w=1;
char ch=getchar();
while(ch<'0' || ch>'9') {if(ch=='-') w=-1;ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<3)+(X<<1)+ch-'0',ch=getchar();
return X*w;
}
inline ll lread()
{
ll X=0,w=1;
char ch=getchar();
while(ch<'0' || ch>'9') {if(ch=='-') w=-1;ch=getchar();}
while(ch>='0' && ch<='9') X=((X<<3)+(X<<1)+ch-'0')%p,ch=getchar();
return X*w;
}
void print(int x)
{
if(x<0)
{
putchar('-');
x=-x;
}
if(x>9)
{
print(x/10);
}
putchar(x%10+'0');
}
int main()
{
in(n);in(m);
for(int i = 1;i <= n;i++)
in(v[i]);
f[0][0][0][0] = v[1];
for(int i = 1;i <= m;i++)
{
int t;
in(t);
w[t]++;
}
for(int a = 0;a <= w[1];a++)
{
for(int b = 0;b <= w[2];b++)
{
for(int c = 0;c <= w[3];c++)
{
for(int d = 0;d <= w[4];d++)
{
int r = 1+a+b*2+c*3+d*4;
if(a != 0) f[a][b][c][d] = max(f[a][b][c][d],f[a-1][b][c][d] + v[r]);
if(b != 0) f[a][b][c][d] = max(f[a][b][c][d],f[a][b-1][c][d] + v[r]);
if(c != 0) f[a][b][c][d] = max(f[a][b][c][d],f[a][b][c-1][d] + v[r]);
if(d != 0) f[a][b][c][d] = max(f[a][b][c][d],f[a][b][c][d-1] + v[r]);
}
}
}
}
out(f[w[1]][w[2]][w[3]][w[4]]);
return 0;
}
这道题用到并查集+二分图染色思想（只用了思想没用任何相关算法）。
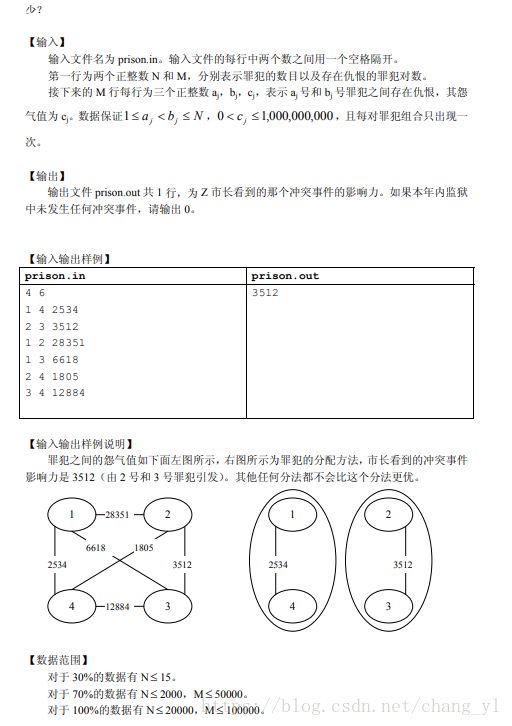
个人来说没想到并查集，导致模拟贪心直接爆炸。
总而言之，这题就类似于某道名为食物链的题，只是多了贪心要最小值。
贪心主要就是每次都拆怨气最大的俩位狱♂友，知道不行了肯定就上报那个怨♂气最大的嘛。
1、看到代码就知道，我把并查集多开了n个节点，相当于俩监狱。
2、priority_queue，最小堆来贪心。
3、并查集操作，都把现在点祖先赋为另一个监狱的点，可以想到发现俩点祖先为一个时说明肯定两人只能在同一个监狱了，于是输出（因为贪心最小堆的缘故找到一个肯定是接下来中最大的了直接输出结束程序就好）。
4、特判，没有怨气就输出0。
代码中还是有些细节说不太清，大家看看吧。
#include
using namespace std;
#define RG register
#define ll long long
#define in(x) x = read()
#define lin(x) scanf("%lld",&x)
#define llin(x) x = lread
#define din(x) scanf("%lf",&x)
#define dout(x) printf("%lf",x)
#define out(x) print(x)
#define lout(x) printf("%lld",x)
#define ex putchar('\n')
#define ko putchar(' ')
const ll p = 1e10 + 7;
const int MAXN = 1e5 + 5;
int n,m;
inline int read()
{
int X=0,w=1;
char ch=getchar();
while(ch<'0' || ch>'9') {if(ch=='-') w=-1;ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<3)+(X<<1)+ch-'0',ch=getchar();
return X*w;
}
inline ll lread()
{
ll X=0,w=1;
char ch=getchar();
while(ch<'0' || ch>'9') {if(ch=='-') w=-1;ch=getchar();}
while(ch>='0' && ch<='9') X=((X<<3)+(X<<1)+ch-'0')%p,ch=getchar();
return X*w;
}
void print(int x)
{
if(x<0)
{
putchar('-');
x=-x;
}
if(x>9)
{
print(x/10);
}
putchar(x%10+'0');
}
struct NODE
{
int x,y,val;
};
struct cmp
{
bool operator()(const NODE& a,const NODE& b)
{
return a.val < b.val;
}
};
priority_queue,cmp>gx;
int ant[MAXN];
int Find(int x)
{
if(ant[x] != x)
return ant[x] = Find(ant[x]);
return x;
}
int main()
{
in(n);in(m);
for(int i = 1;i <= 2*n;i++) ant[i] = i;
for(int i = 1;i <= m;i++)
{
int a,b,c;
in(a);in(b);in(c);
gx.push((NODE){a,b,c});
}
while(!gx.empty())
{
if(Find(gx.top().x) == Find(gx.top().y))
{
out(gx.top().val);
return 0;
}
int tx = gx.top().x;int ty = gx.top().y;
ant[ant[tx]] = ant[Find(ty+n)];
ant[ant[ty]] = ant[Find(tx+n)];
gx.pop();
}
cout << 0;
return 0;} 
一道搜索题（虽然可以优化为动规但是其实记忆化深搜和广搜都能过。。）
总的来说，只要能实现判断第一行到最后一行的算法就都行。
实际上这道题铺水的（可以理解为染色吧，能输到水的就是被染了色）最后一行的线段一定是切合在一起的，（如果不这样的话很明显看出中间会差一截不能完成。）所以我们可以就此用一个动规思想得到每个点能到的最左和最右，从而得到最后一行的最左和最右。
然后最后遍历一下最后一行就行。
具体还是看代码吧，毕竟实现方法很多，这是其中一种罢了：（注意宏定义，比较懒）
#include
using namespace std;
#define RG register
#define ll long long
#define in(x) x = read()
#define lin(x) scanf("%lld",&x)
#define llin(x) x = lread
#define din(x) scanf("%lf",&x)
#define dout(x) printf("%lf",x)
#define out(x) print(x)
#define lout(x) printf("%lld",x)
#define ex putchar('\n')
#define ko putchar(' ')
const ll p = 1e10 + 7;
const int MAXN = 505;
#define addx x + xx[i]
#define addy y + yy[i]
int xx[4] = {-1,0,1,0};
int yy[4] = {0,1,0,-1};
int n,m;
int cnt = 0;
int h[MAXN][MAXN];
int l[MAXN][MAXN],r[MAXN][MAXN];
bool vis[MAXN][MAXN];
bool flag = 0;
inline int read()
{
int X=0,w=1;
char ch=getchar();
while(ch<'0' || ch>'9') {if(ch=='-') w=-1;ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<3)+(X<<1)+ch-'0',ch=getchar();
return X*w;
}
inline ll lread()
{
ll X=0,w=1;
char ch=getchar();
while(ch<'0' || ch>'9') {if(ch=='-') w=-1;ch=getchar();}
while(ch>='0' && ch<='9') X=((X<<3)+(X<<1)+ch-'0')%p,ch=getchar();
return X*w;
}
void print(int x)
{
if(x<0)
{
putchar('-');
x=-x;
}
if(x>9)
{
print(x/10);
}
putchar(x%10+'0');
}
void dfs(int x,int y)
{
vis[x][y] = 1;
for(int i = 0;i < 4;i++)
{
if(addx < 1 || addx > n || addy < 1 || addy > m) continue;
if(h[addx][addy] >= h[x][y]) continue;
if(!vis[addx][addy]) dfs(addx,addy);
l[x][y] = min(l[x][y],l[addx][addy]);
r[x][y] = max(r[x][y],r[addx][addy]);
}
}
void work()
{
for(int i = 1;i <= m;i++)
{
if(!vis[1][i]) dfs(1,i);
}
for(int i = 1;i <= m;i++)
if(!vis[n][i])
{
flag = 1;
cnt++;
}
if(flag)
{
cout << 0;
ex;
out(cnt);
return;
}
int le = 1;
while(le <= m)
{
int maxr = 0;
for(int i = 1;i <= m;i++)
if(l[1][i] <= le)
maxr = max(maxr,r[1][i]);
cnt++;
le = maxr+1;
}
cout << 1;
ex;
out(cnt);
}
void init()
{
in(n);in(m);
memset(vis,false,sizeof(vis));
memset(l,0x3f,sizeof(l));
memset(r,0,sizeof(r));
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
in(h[i][j]);
for(int i = 1;i <= m;i++)
l[n][i] = r[n][i] = i;
}
int main()
{
init();
work();
return 0;
}