算法基础 - 求有向图的强连通分支(Tarjan算法)

强连通分支

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

Tarjan算法

Tarjan算法是用来求有向图的强连通分量的。求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法。

流程

对有向图先任取一个节点，只要这个节点没被遍历过，则从其开始进行深度优先遍历。这里记录两个数组，dfn[i] and low[i]，其中dfn[i]很容易理解，就是在是深度遍历的时候，遍历到第i个节点的时候，当前是第几个遍历到的节点，也就是说这个遍历序列的位置。第一个遍历到就是1，遍历到第10个节点的时候，遍历到就是10,相当于时间戳。

还有low[i]，这个就比较难理解了，其实这个记录的是，当前这个节点i最远能到之前哪个节点， 例如在图里面有一个环：1->2->3->4->1那么low[4] = dfu[1]，但是假如还包括一条变4->2，那么指向谁呢？ 答：指向小的那个！ 也就是找最大的强连通分支。

例子

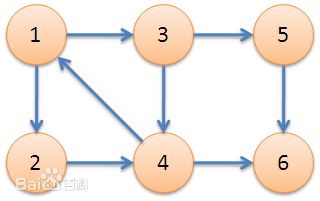
首先我们看这个图，先用肉眼找一下强连通分支，分别是：{1,2,3,4}, {5}, {6}这三个强连通分支

那么对图开始遍历，对于深度遍历，首先从1开始，一直遍历到6.
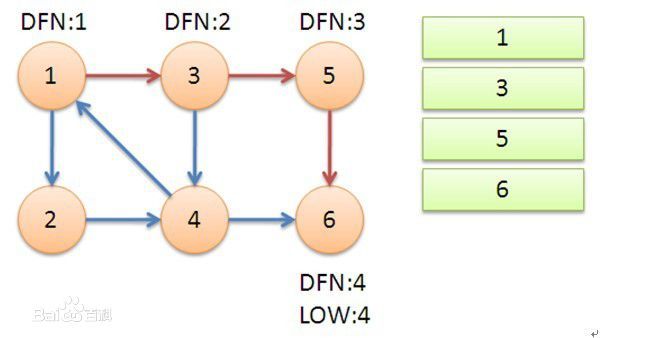
发现6到头了，然后比较当前节点是不是一个强连通的分支的根( dfu[i] == low[i] 就是)，发现是的，弹栈知道刚好6弹出栈。所弹出栈的所有节点，就是第一个子强连通图：{6}

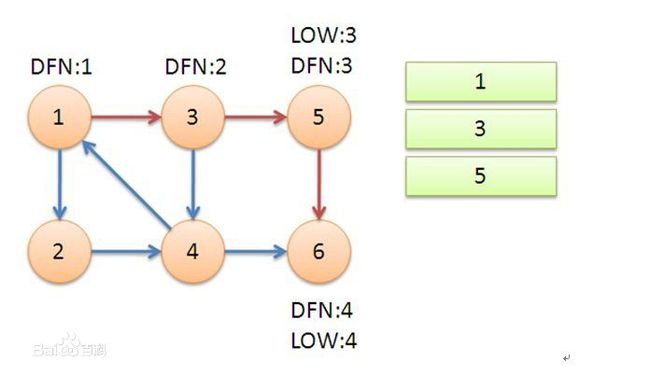
对于5 我们得到low[5] = min(low[5], low[6])，这样发现，5也是一个根，则弹栈得到：{5}，然后弹栈到3，得到low[3] = min(low[3], low[5]) = 2

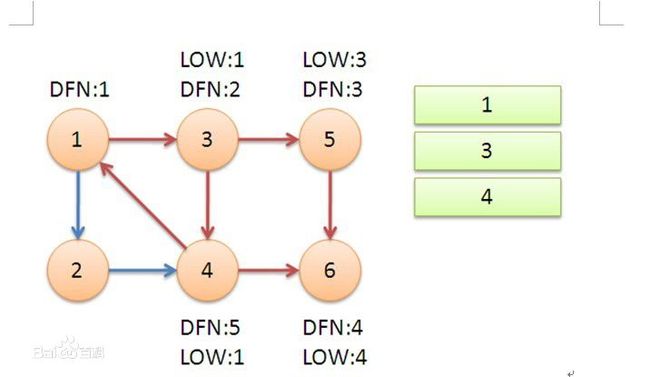
然后3号节点走到4号节点，继续走到1号节点，发现1号已经在栈里面了，说明找到一个强连通分支了，那么让low[4] = min( low[4], dfn[1] )这里是意思是让low[4]最小，也就能找到最大的环。4走完了之后（不走6 因为6是已经遍历过的节点，并且不在栈里面），弹栈，到3，3发现也走完了，得到low[3] = min(low[3], low[4]) = 1，然后弹栈到1，low[1] = min(low[1], low[3])

再然后遍历节点2，遍历到4的时候发现，也已经遍历过了，但是4在栈里面，那么low[2] = min(low[2], dfn[4]) = 5

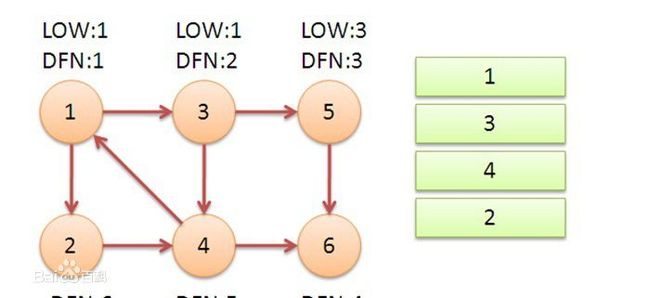
然后深度遍历完了，回退到1号节点，发现dfn[1] == low[1]就开始弹栈，得到第三个强连通分支：{1, 2, 3, 4}

代码

#include 
#include 
#include 
#include 
#include 


using namespace std;

#ifndef MAXNODE
#define MAXNODE 20005
#endif

int flag[MAXNODE] = {0}; //判断图中的点是否在栈内
int dfn[MAXNODE] = {0}; //dfu数组
int low[MAXNODE] = {0}; //low数组
int tpArr[MAXNODE] = {0}; //存放节点属于第几组联通图
int tpNum = 0; //对强连通分支设置ID
int _index = 0; //dfs遍历的ID

vector<int> graph[MAXNODE]; //图

stack<int> st; //栈

void tarjan(int n){
    st.push(n);
    flag[n] = 1;
    dfn[n] = ++_index;
    low[n] = _index;
    for (int i = 0; i < graph[n].size(); i++) {
        int cur = graph[n][i];
        if (dfn[cur] == 0) {
            tarjan(cur);
            low[n] = min(low[n], low[cur]);
        }else{
            if (flag[cur] == 1) {
                low[n] = min(low[n], dfn[cur]);
            }
        }
    }
    if (dfn[n] == low[n]) {
        tpNum++;
        do{
            n = st.top();
            st.pop();
            flag[n] = 0;
            tpArr[n] = tpNum;
        }while(dfn[n] != low[n]);
    }
}

测试添加图的代码：

int main(){
    int N,T; //节点总数和边数 节点ID从1开始
    cin>>N>>T;
    int s,e;
    for(int i = 0;i < T; i++){
        cin>>s>>e;
        graph[s].push_back(e);
    }
    for(int i = 1; i <= N; i++){
        if(dfn[i] == 0){
            tarjan(i);
        }
    }
    for(int i = 1; i <= N; i++){
        cout<' ';
    }
    return 0;
}

自己可以按照上面的图输入一下。

这个算法可以解决2-sat问题