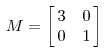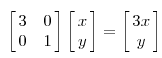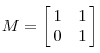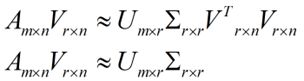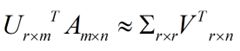《推荐系统实践》阅读笔记三 LFM模型、图模型、slop one和SVD算法

2.5 隐语义模型

LFM（latent factor model）。表示一类模型，有很多经典的模型，如：LSI、pLSA、LDA和topic model等。

LFM优势：

面对商品分类的时候，人工编辑给出的类别有很多缺点，如不好解决一物多类问题、不好设定物品与类别的权重、主观性因素太强等等。LFM由于其模型本身，能够有效地避免上述问题。

我们可以对书和用户兴趣进行分类，对于某个用户，可以首先得到他的兴趣分类，然后从分类之中挑选他可能喜欢的物品。而LFM就可以自动的给物品进行分类，并且确定用户对哪些类的物品感兴趣，以及感兴趣的程度。

LFM使用选择：

LFM在显性反馈数据（评分数据）上取得了良好的精度。在隐形反馈数据上，需要面临的问题是如何选择负样本，作者有两点建议：（1）对每个用户，保证正负样本数目相似；（2）采集负样本的时候，尽量选取物品本身很热门，但是用户没有行为的物品——这更说明了用户“不喜欢”这类物品。

参数：

LFM在训练过程中的参数有四个：（1）隐含类别个数；（2）学习速率；（3）正则化参数（防止过拟合）；（4）正负样本比例。实践证明，参数（4）对模型的性能影响最大。参数（4）控制了推荐算法挖掘长尾物品的能力——负样本比例越高，准确率、召回率越高，但是覆盖率越低。

LFM和基于邻域的算法的比较

1. UserCF和ItemCF的空间复杂度较大。

2. 离线计算时间两者相当，LFM会更加费时，但是没有质的差别。

3. LFM给用户推荐列表结果比较慢，不适合实时系统。如果应用在实时系统，也是先用别的方法给用户一个小的结果集合，然后LFM再优化排序。

4. ItemCF有很好的推荐理由，UserCF和LFM则没有。

5. 数据集稀疏的时候LFM的性能会明显下降。

2.6 图模型

推荐系统其实就是搞清楚用户和物品之间的关系。而这两者之间可以用二分图来表示。推荐的任务就是，对于用户节点U和他没有拥有的物品节点集合Set(items)，计算集合中每一个元素与用户节点U之间的关联程度。计算方式可以采用图的算法。

考虑因素：

设计算法的时候，有几个因素需要考虑：（1）顶点之间的路径数目；（2）顶点之间的路径长度；（3）路径经过了哪些顶点。

随机游走算法，PersonalRank算法，具体算法见书中描述。感觉和pagerank、Hits算法等类似。什么东西转化成了图，都可以“随机游走”。

该算法的时间复杂度非常高。

优化方法：

（1）减少迭代次数，会影响精度，不过从实践中检验，影响不会太大；（2）从矩阵论出发，重新设计算法。

2.7 Slop one算法

Slop one 算法思想简单，如果A, X ,Y 对Item1打了1分，用户X，Y还对Item2打了分，问用户A对item2的可能打分是多少？

User	Rating to Item 1	Rating to Item 2
X	5	3
Y	4	3
A	4	?

 根据SlopeOne算法, 应该是:4 - ((5-3) + (4-3))/2 = 2.5.

因为用户X对item2比item1少打了2分，用户Y对item2比item1少打了1分，那么我们认为item2得到的评分比item1的平均值要小1.5分。我们可以根据这里计算用户A对item2的评分。

SVD算法

SVD奇异矩阵分解是线性代数中一种重要的矩阵分解，在信号处理、统计学中都有重要的应用。奇异值分解在某些方面与对称矩阵或者Hermite矩阵基于特征向量的对角化类似。然而这两种矩阵分解尽管有相关性，但是还有明显的不同。对称矩阵特征向量分解的基础是频谱分析仪，而奇异值分解则是谱分析理论在任意矩阵上的推广。

总而言之，SVD算法在很多地方都有广泛的应用。比如feature reduction的PCA， 数据压缩的算法，还有搜索引擎语义层次检索的LSI，还有推荐系统的Latent Factor Model。

首先我们来复习一下什么是特征值分解：

1）特征值：

如果说一个向量v是方阵A的特征向量，将一定可以表示成为下面的形式：

                                                                      

这个时候λ就被称为特征向量v对应的特征值，一个矩阵的特征向量是一组正交向量。特征值分解是将一个矩阵分解成为下面的形式：

                                                      

其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角矩阵，每个对角线上的元素就是一个特征值。其实一个矩阵就是一个线性变化，因为一个矩阵可以乘以一个向量后得到的向量。其实就相当于将这个向量进行了线性变换。比如说下面这个矩阵：

                                           

它对应的线性变化是下面这种形式：

                                      

我们通过计算得到的M乘以一个向量(x,y)的结果是：

                                     

这实际上是对向量x,y的一个伸缩变换。对x轴拉伸3倍，对y轴不做任何变换。

而当矩阵是不对称的时候如下图所示：

                                      

它描述的变换是下面的样子：

这其实是在平面上对一个轴进行拉伸变换，在图中，蓝色的箭头是最重要的变化方向。如果我们想要描述好一个变换，那么我们就描述好这个变换的主要方向就好了。反过来看之前的特征值分解的式子，分解得到的矩阵是一个对角矩阵，里面的特征是是由大到小排列的，这些特征值所对应的特征值响亮就是描述这个矩阵变化的方向（从主要的变化到次要的变化排列）。

当这个矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换同样也有很多个方向。我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵主要的N个变化方向。我们利用这前N个变化的方向就可以近似这个矩阵的变换。也就是之前所说的提取矩阵的最主要特征。总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

2）奇异值：

下面谈谈奇异值分解。特征值分解是一个提取矩阵特征很不错的方法。但是它只是对方阵而言，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有N个学生，每个学生有M科成绩，这样形成的N*M的矩阵可能不是方阵。我们怎样才能描述这种矩阵的重要性质呢？奇异值分解可以干这样的事情，奇异值分解可以适用于任意矩阵的分解：

那么奇异值和特征值是如何对应起来的呢？首先，我们将一个矩阵的转置*A，将会得到一个方阵，我们用这个方阵求特征值可以得到：

这里得到的v，就是我们上面所说的右奇异向量。我们还可以得到：

这里的就是上面所说的奇异值，u就是上面所说的左奇异向量。奇异值跟特征值类似，在矩阵中也是从大到小排列，而且得减少特别快。在很多情况下，前10%甚至1%的奇异值的和就占到了全部奇异值之和的99%。也就是我们可以使用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：

r是一个远小于m、n的数，这样矩阵的乘法如下：

奇异值计算是一个难题，因为复杂度O(n^3)，计算复杂度成3次方增长。谷歌实现了并行化的SVD算法，MapReduce和MPi。还有Lanczos迭代，就是一种解对称房展部分特征值的方法，是将一个对称的方程转化为一个三对角矩阵再进行求解。

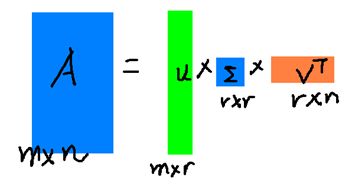
左边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这里，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和要远小于院士矩阵A。我们如果想要压缩矩阵存储空间来存储元素矩阵A，我们存下如下三个矩阵：U、Σ、V就好了。

其实针对PCA问题来说，前面的等式两边乘以V，就转化为：

我们可以从一个m行的矩阵压缩为一个r行的矩阵，这对SVD来说也是一样的。我们将SVD矩阵分解的两边同时乘以U'。就可以得到：

PCA几乎是对SVD的一个包装。

2）SVD与LSI

LSI（Latent Semantic Indexing）隐语义模型，是近些年来兴起的基于关键字索引的搜索引擎解决方案。其检索的实际效果更加接近人的自然语言。一定程度上增加了检索结果的相关性。目前已经得到了广泛的应用。

它的使用步骤：

（1）先统计、分析网页及链接中的关键词；

（2）将该网页与索引数据库中其他包含相同关键词或部分相同关键词的网页进行比对，以确定不同网页间的语义相关性以及网页与特定关键词间的相关性，

（3）同时将该网页与具有高语义相关性的网页进行比对分析，从中找出特定网页中存在关键词的相关项，即找出特定网页中虽然并不存在但与其内容相关的关键词。

3）SVD与推荐系统

SVD（Singluar Value Decomposition）的想法是根据已有的评分情况，分析出评分者对各个因子的喜好程度以及电影包含的各个因子的成都再反过来分析结果预测的评分的。SVD得出的奇异向量也是从奇异值由大到小排列的，按照PCA的规定来看就是方差最大的一个是第一个奇异向量，以此类推。

SVD矩阵分解的示意图：

     首先我们讲一个矩阵A转置A*，将会得到一个方阵，我们再对这个方阵求特征值可以得到：

这里得到v，就是我们上面的右奇异向量，此外我们还可以得到：

这里的这里的σ就是上面说的奇异值，u就是上面所说的左奇异向量。奇异值σ跟特征值类是，矩阵Σ中也是从大到小排列的，而且σ见效的也特别快，在很多情况下前10%甚至1%的奇异值和就占到了全部的奇异值和的99%以上了。也就是说，我们也可以用前r打的奇异值来近视描述矩阵，这里定义一下部分奇异值分解：

r是一个远小于m、n的数，这样矩阵的乘法看起来像是下面的样子：

现在可以使用U、Σ、V代表源矩阵，而且存储空间小。。。

未完待续。

User based CF 和 Item based CF 对比：

1 User based 看你好友买了什么东西， Item based看你之前买过什么东西。

2 User CF冷启动问题不像 Item based那么明显。所以User CF很适合像新闻，音乐推荐推荐这种实时性的东西。而item CF比较适合像购物推荐这种。因为新闻之类的实时性很强，而且很难挖掘一个文章或者新闻的受欢迎程度的。

3  Item based 一般迭代要快一些，因为物品一般比较少的么。

LDA算法简介：

参考文献：

LDA模型简介：http://cos.name/2010/10/lda_topic_model/

使用LFM模型进行TopN推荐 http://blog.csdn.net/harryhuang1990/article/details/9924377

LDA模型：http://wenku.baidu.com/link?url=JMIDiNQ4QeaBa9nfH4SwUt8JjaNV61mX_uCiVGXu5tdNTs3TgffMs7YKQMFMgqTikRYTPejq0eyc2Pwv3IobY027s1ficMLsUMSVTn4Teue

先验概率与后验概率及贝叶斯http://wenku.baidu.com/view/fe84f83143323968011c9276.html