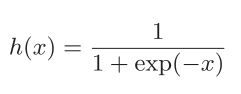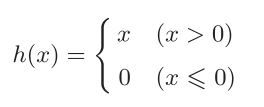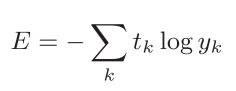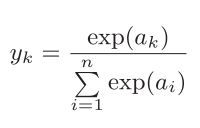卷积神经网络python实现（1）

目录

1、网络结构

2、各层详解

1）卷积层（conv）

A、概念解释

B、实现过程

C、多维输入数据计算

D、卷积层代码实现

2）池化层（pooling）

A、实现过程

B、池化层代码实现

3）激活层

A、sigmoid函数

B、阶跃函数

C、relu函数

4）affine层

5）dropout层

6）softmax-with-loss层

A、损失函数介绍

B、softmax-with-loss层结构介绍

C、代码实现

---

1、网络结构

11层卷积网络结构如下：

conv - relu - conv - relu - conv - relu - pool -

conv - relu - conv - relu - conv - relu - pool -

conv - relu - conv - relu - conv - relu - pool -

affine - relu - dropout - affine - dropout – softmaxwithloss

conv：卷积层

relu：激活层

pool：池化层

affine：全连接层，实现输入数据和节点参数矩阵的相乘

dropout：按照一定概率抛弃某些节点，防止过拟合

softmax-with-loss：将输入数据正规化后输出，并输出交叉熵误差

2、各层详解

1）卷积层（conv）

A、概念解释

填充（pad）：卷积运算前，想输入数据周围填入固定的数据（比如0），用P表示。

步幅（stride）：应用滤波器的窗口间隔大小。

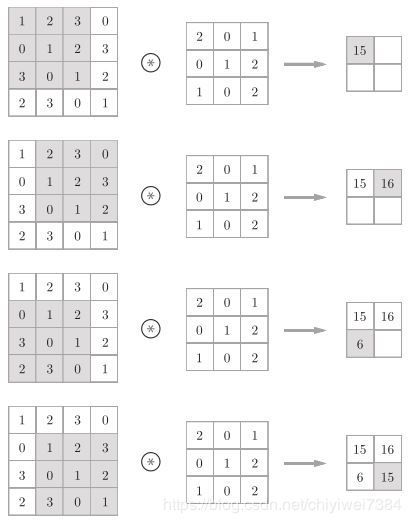
B、实现过程

如图1

                                           图1

假设待处理矩阵大小为 ( W , H ) ，卷积滤波器大小为 ( FW , FH ) ,填充为P，步幅为S，则输出矩阵大小为：

                                      

C、多维输入数据计算

实际应用中，输入多为三通道彩色图像，此时滤波器相应设为三通道，即：

 

通过im2col函数将四维矩阵展开为二维矩阵进行运算，函数形式如下：

                         col = im2col(x, FH, FW, self.stride, self.pad)

x为输入矩阵，输出矩阵的大小为

                             ( OH * OW * N ,  FH * FW * C )

D、卷积层代码实现

2）池化层（pooling）

A、实现过程

                                                                       图2

池化层滤波器大小一般为（2 , 2），随着滤波器的移动，依次选择窗口内的最大值作为输出。

B、池化层代码实现

处理多维数组时，依然用im2col函数改变维度以方便计算。

3）激活层

激活函数一般用非线性函数，本节介绍常用的几种激活函数。

A、sigmoid函数

函数形式如下：

Python代码实现：

B、阶跃函数

Python代码实现：

C、relu函数

函数形式如下：

Python代码实现：

本文所构建网络选用relu函数作为激活函数。

4）affine层

前文提到，affine层主要作用时实现矩阵的乘法运算。

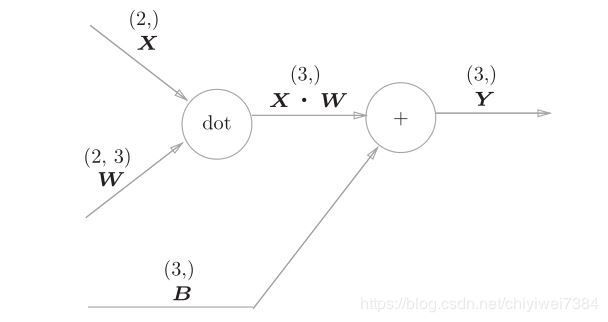
                                                              图3

图3为affine层的计算图，X , W , B 分别为输入数据，节点参数，偏置。

Affine层代码实现：

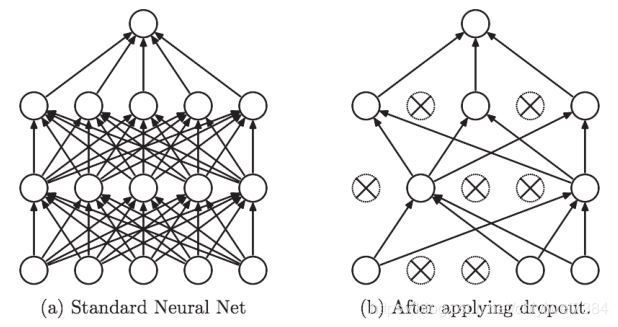
5）dropout层

Dropout是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递，如图4所示。训练时，每传递一次数据，就会随机选择要删除的神经元。然后，测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。

                                                                 图4

Dropout层python代码实现：

6）softmax-with-loss层

A、损失函数介绍

常用的损失函数包括均方误差和交叉熵误差。均方误差的计算公式如下：

这里，yk 是表示神经网络的输出，tk 表示监督数据，k表示数据的维数。E值越小，代表输出与监督数据越吻合。

cross-entropy-error层的输出为交叉熵误差，计算公式如下：

这里，log表示以e为底数的自然对数（log e ）。yk 是神经网络的输出，tk 是正确解标签。并且，tk 中只有正确解标签的索引为1，其他均为0 。因此，上式实际上只计算对应正确解标签的输出的自然对数。比如，假设正确解标签的索引是“2”，与之对应的神经网络的输出是0.6，则交叉熵误差是−log0.6 = 0.51；若“2”对应的输出是0.1，则交叉熵误差为−log0.1 = 2.30。也就是说，交叉熵误差的值是由正确解标签所对应的输出结果决定的。

B、softmax-with-loss层结构介绍

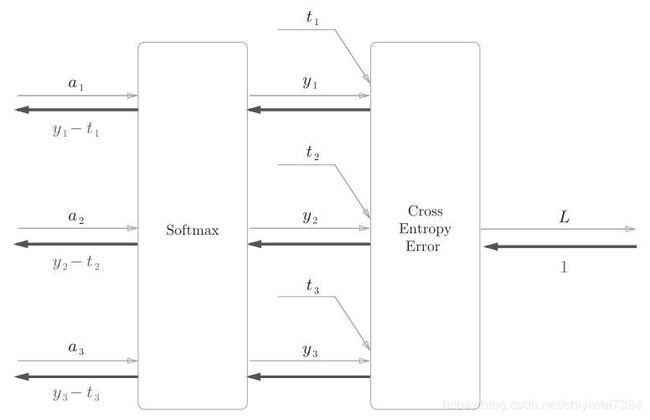
该层的计算图如图5所示。softmax-with-loss层包括正向传播和反向传播，本节先介绍正向传播。

                                                                              图5

softmax-with-loss层由softmax、cross-entropy-error两个函数构成。Softmax层的作用为将输入正规化输出，计算公式如下：

如图6，Softmax层将输入值正规化（将输出值的和调整为1）之后再输出。另外，因为手写数字识别要进行10类分类，所以向Softmax层的输入也有10个。

                                       图6

Softmax层代码实现：

C、代码实现