基于存储证明(Proof of storage)的Permacoin挖矿原理解析
过去的一周让人感觉五味杂陈,心力交瘁,工作非常忙,非常累,非常没有进展,时而芳香,时而谢特,本想着这周末什么也不干撸点没意义的事情度日呢,然而还是觉得把意义拆散来的可靠些。所以依旧很早爬起来总结一下过去一周上下班路上的思考。
序
既然我无法把家里的幸福感代入进工作,我也尽量不把这种工作上的挫败感带到家里,因此我只能在上下班的路上来点既和工作无关又和家庭无关的东西,作为一个缓冲区。最近一个月的主题是区块链而不是古罗马帝国历史。
利用路上的时间,我学习了区块链的基本原理和应用,但这些并没有让人兴奋,让人兴奋是一种叫做Permacoin的币种,其设计之巧妙让人叹为观止,不知怎地,看到这个就好像当年看到Skip List一般,简单,直接,容易理解。这是让我忍不住写下本文的第一个原因。
为什么写下本文还有一个原因,昨晚和朋友交流技术,很多尘封已久的故事恍如昨日涌上心头,在高中的时候同学们普遍觉得我的物理学的是最好的,But I tell them No,我最喜欢的其实是数学。今天我又一次发现,虽然我最喜欢折腾Linux Netfiler,然而我可能表现的更擅长TCP优化,如今,我差一点因为整日声称自己是华南Kafka第一人而卷入风波惹事端,唉,以后还是保持缄默。所以我不得不写一点其它方面的东西吸引一下自己的注意力。
本文依然是技术散文,而非Howto。Let’s go!
何为Permacoin
Permacoin是一个微软研究院和美国马里兰大学联合提出的与比特币竞争的币种,其特点主要在于,它的挖矿行为并非注释纯粹的工作量证明,除此之外必须加入一种有意义的担保,即对挖矿矿工的资格进行了某种限定。这正如很多大型企业招聘明确要求必须是985本科以上学历是一样的。
Permacoin认为,如果矿工不做一些有意义的事,那么它将失去挖矿资格。其挖矿行为就在于矿工要证明这种需要表达的意义。
就这么简单的道理,其背后的数学原理是非常值得鉴赏的,它很简单,优美,高雅,整个过程正如行云流水一般让你纵享丝滑。我从Permacoin进化的最开始说起,依然是见招拆招的方式来试图解决我在分析中碰到的任何问题。
为了理解Permacoin的实际意义,让我们从浪费来说起。
何为浪费
最初接触比特币的时候,让我想不通的是,一大堆硬件全功率奔徙挖矿,就是为了反算一个哈希,为此还形成了若干的矿池,为了获得廉价的电力资源以及廉价的制冷装备,这些矿池不得不建设在类似中国川西这种水电资源丰富且廉价的地区或者北欧这种足够冷又不至于结霜的地方…和类似BAT的那种大型IDC机房不同,这些矿池不产生任何业务数据,只是为了反算哈希,这些设备除了产生大量无法利用的热量之外,不会有任何用途!这值得吗?
几乎所有的人都会想当然认为这是一种浪费,但是想象一下下一代以及再下一代人,当他们在比特币系统的进化过程中长大并且普遍使用比特币作为支付手段以后,他们可能就会认为我们这一代人所谓的浪费是一种理所当然,不是吗?其实我们所有的人都在走着老路。日光之下,并无新事,我们也一样。
当第一家银行产生的时候(当然,这是一个缓慢的过程),人们不禁也会把银行的管理设施和某种浪费关联起来。直到现在,我们中的很多人(比如我)依然想不通为什么银行的大楼必须建的如此豪华,为什么银行员工的衣着必须如此昂贵体面,为什么银行的人不能穿廉价的拖鞋短裤T恤上班,然而可能薪资收入更高的互联网企业却完全可以随意。这难道不是一种浪费吗?难道一间简陋的小屋里,一群拖鞋短裤的金融精英在一起就不能处理银行业务吗?
和比特币挖矿一样,银行机构所谓的这种高大上的铺张浪费其实也是在建立一种共识,让所有人觉得这家银行靠谱,值得信赖,它有足够的资本让我相信我把钱放它那里后是安全的,其实仅此而已。你以为那些人穿着西装皮鞋,扎着领带舒服吗?他们在炎热的夏天必须穿在那个季节看起来厚厚的西装,扎着领带,这意味着空调温度必须打的足够低才能不让他们难受,同样,在寒冷的冬天,他们依然是那些行头,这意味着需要同样的电力供应使他们舒适而不至于受冻。银行不能开窗,不能让风把桌面和发型吹得凌乱从而有失体面,因此需要新风系统的能源持续供应,这一切的浪费在其它很多行业都是可以避免的。
和比特币挖矿的浪费相比,是不是银行的浪费更可怕呢?不光是在大多数人看来没有意义的电力消耗,还有人的精神上的消耗,这一切怎么解释呢?我们说,对于个体,那最重要的就是血液,生死为大,不可不察,而对于社会而言,其血液就是金融,金融为大,天经地义。即便最残酷的战争,说到底拼的还是金融实力。
我上面扯了一通后,也许你会对比特币挖矿浪费行为的怨言有所释怀。但是接下来我要说的,是比特币挖矿在产生这种浪费的同时,还可以做一些有意义的事情。
去中心化分布式存储
互联网时代,idear遍地开花,只有想不到没有做不到的。这不,分布式存储和去中心化一结合,就成就了Permacoin。本节先不谈Permacoin,先说说分布式存储。
分布式存储早就有了,但是一直很难做到去中心化,必须有一个执行中心来执行存储流程,比如类似把文件从m到n这一段存在位置P这种。如果能做到去中心化的分布式存储,世界就更加美妙了。当有人问你,你的文件 F F 存在哪里的时候,你的回答是,它存在全世界,虽然也不知道它具体存在哪里…最终我们的愿景是,任何人可以在任何设备上存储任何人的任何文件的任何部分,数数几个“任何”…但情况确实如此!
可是,问题来了,别人凭什么帮你存文件,一个合理却不现实的解释是,我也帮别人存了文件,但这不是一个人人为我,我为人人的社会,这是一个自私的社会,因此采用更加直接的办法反而更能行得通,那就是谁帮我存文件,我给谁钱,毕竟,你买类似Dropbox这样的存储服务,不也是要花钱的么?
好的,现在剩下两个问题:
1. 如果我不知道他是谁,怎么把钱给他;
2. 我把钱给他,怎么证明他真的帮我存了文件而没有欺骗我。
针对上述两个问题的回答,将会导出一个合理的分布式存储的去中心化方案。接下来就简单描述一下该方案。
Merkle树
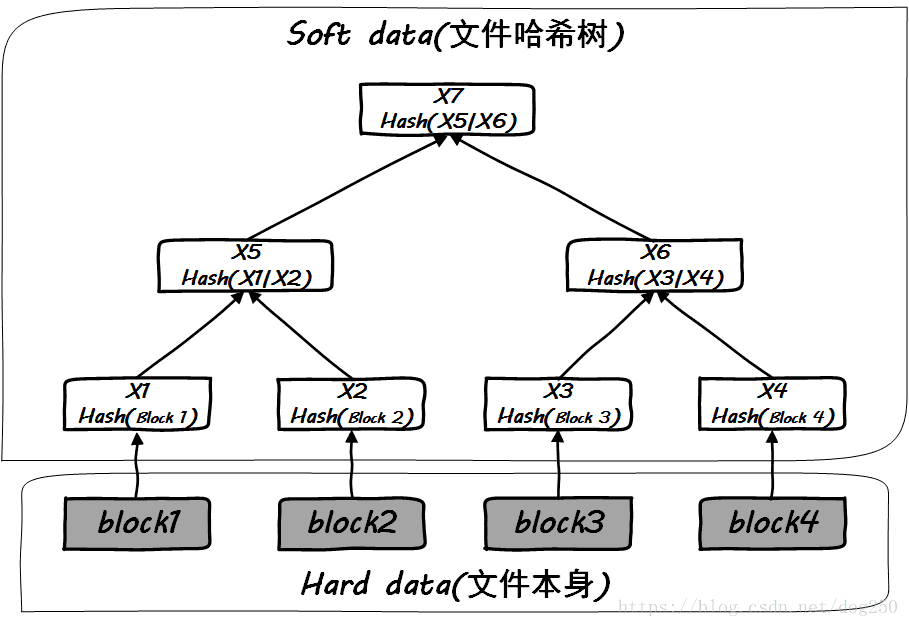
为了证明自己拥有某个文件或者文件块,在网络上直接传输该文件块本身,想必是一件效率很低的事情,然后Merkle树利用哈希函数的抗碰撞特性解决了这个问题。以下是一棵关于文件 F F 的Merkle树:
与直接传输文件块本身不同,有了Merkle树之后,我们传输文件块的哈希值即可。只要可以沿着从叶子到根的路径上全部通过,则可以证明自己拥有该文件。为了简单起见,我们假定,文件不再分割成文件块,而是整体存储。
对于去中心化分布式存储,一个问题就是如何辨别所谓的存储者是真的存了文件,还是只是算好了哈希值并保存后把源文件删除(节省自己的存储资源)。这就需要一个挑战/应答机制。
挑战/应答
文件 F F 的拥有者,即属主向帮存者发起一个挑战:
设文件F被分割为N块,s为集合{1,2,...N}中随机的任意值,r为任意随机数,则: 设 文 件 F 被 分 割 为 N 块 , s 为 集 合 { 1 , 2 , . . . N } 中 随 机 的 任 意 值 , r 为 任 意 随 机 数 , 则 :
challenge=(F[s]||r) c h a l l e n g e = ( F [ s ] | | r )
帮存者收到这个 challenge c h a l l e n g e 之后,会怎样产生一个应答呢?
如果帮存者真的保存了这个文件,那么它就可以拿出 F[s] F [ s ] 文件块的哈希值,然而还要更进一步,它完全可以在不久前私下保存了所有文件块的哈希值后把文件删除了,此时, challenge c h a l l e n g e 中的 r r 就派上了用场,文件属主不仅仅要求帮存者回答 F[s] F [ s ] 文件块的哈希值,还要求它做以下的运算:
h=H(F[s]||r) h = H ( F [ s ] | | r )
这样一来,即便它保存了 F[s] F [ s ] 文件块的哈希值也没卵用,随机数 r r 会打乱一切,除非它真的保存有 F[s] F [ s ] 文件块,不然它反算这个哈希值的难度将会非常大,几乎是不可能的。所以说,帮存者需要回复下面的应答:
response=(h||πF[s]) r e s p o n s e = ( h | | π F [ s ] ) (πF[i]为F[i]的哈希值) ( π F [ i ] 为 F [ i ] 的 哈 希 值 )
文件属主收到后将会做一系列的校验。首先属主肯定有整棵的关于文件 F F 的Merkle树,其次它还保存着原始的 challenge c h a l l e n g e 值,因此它很快就能知道帮存者是否在撒谎。当然,属主可以任何时候发起任意次数的挑战。
也许你要问,仅仅挑战一个或者几个文件块而不是直接挑战整个文件能证明帮存者存储了整个文件吗?确实不能,但这是一个保证和效率之间的权衡问题。如果随机数 s s 足够随机,那么它将均匀分布在集合 {1,2,...N} { 1 , 2 , . . . N } 中,从而让恶意的帮存者无法判断具体的挑战分布,实际中的系统会对撒谎行为进行惩罚,但本文只是理论分析就不再展开。因此对于帮存者而言,最保险的方案就是,整个文件全部帮存。
付款
现在该说如何付款了。
既然属主发起的挑战帮存者都成功应对了,那么该属主付钱了吧。典型直接的方案就是在应答报文里加一个银行卡号,但这会影响匿名性,属主可以拿着银行卡号去查询帮存者的各种信息…这个时候,比特币便是一个很好的付款载体了。
比特币钱包就是一个公钥,因此帮存者的应答只要添加自己的钱包地址就可以了。但是这完备吗?中间被截获了被更改了怎么办?所以说还需要帮存者的私钥签名,因此应答信息成了:
设Kpub为帮存者公钥,用于验证签名,Paddr为帮存者比特币钱包,用于收款,则: 设 K p u b 为 帮 存 者 公 钥 , 用 于 验 证 签 名 , P a d d r 为 帮 存 者 比 特 币 钱 包 , 用 于 收 款 , 则 :
K=(Kpub||Paddr) K = ( K p u b | | P a d d r )
m=(h||πF[s]|K) m = ( h | | π F [ s ] | K ) (πF[i]为F[i]的哈希值) ( π F [ i ] 为 F [ i ] 的 哈 希 值 )
response=(m||Signpriv(m)) r e s p o n s e = ( m | | S i g n p r i v ( m ) )
属主会做如下方法来验证 response r e s p o n s e 的身份真实性:
m=response−Sign m = r e s p o n s e − S i g n
VerifyKpub(m) V e r i f y K p u b ( m )
接下来的校验同上。
冗余分存
以上的论述我自己反复看了几遍,感觉还算清楚,现在我们去掉假设,即不再让一个帮存者帮存整个文件,而只是一个文件的一些部分,可以自行推导,以上的的论述依然适用。
然而通篇到目前,我们只是谈了文件的分存问题,没有涉及文件恢复。由于这是去中心化的完全分布式存储,理论上同一块文件会在多个帮存者那里同等概率被保存,只要帮存者足够多,便不存在文件丢失的问题,但是如果所有保存某个文件块的帮存者结成联盟勒索文件属主索要大额比特币怎么办??这种问题是可以通过技术解决的。
请看我的下面这篇文章了解一下密钥分存技术:
《密钥分存技术(现代虎符)-如何把密钥存在不同的地方》:https://blog.csdn.net/dog250/article/details/79823688
然后我们来看如何应对。
一个方案就是,每一个帮存者不是帮存特定的文件块,而是帮存文件块的部分,这么做的目的就是,假设有 m m 个帮存者存储了文件块 F[i] F [ i ] ,存在自然数 n n (n<m) ( n < m ) ,只需要 n n 个部分就能恢复文件块 F[i] F [ i ] ,具体的原理涉及到了二项式定理以及编码细节,详情参见我上周写的那篇关于密钥分存的文章。
显然,这个方案增强了整个分布式存储系统的容错性,是的文件属主不再依赖特定的帮存者,同时任何一个帮存者均无法独自恢复文件块 F[i] F [ i ] ,大家必须一起对虎符,这会在所有存储同一个文件块 F[i] F [ i ] 的所有帮存者之间形成心理博弈,它们便很难联盟勒索了。
去中心分布式存储的引申
当我第一次看到上面的idear时,我感觉这太棒了,你的文件竟然可以如此存储而保持机密性,同时没有任何一个存储中心可以肆意妄为,这真的很棒。然而更加好玩的是,这个思想竟然可以应用到比特币挖矿行为上。
本文接下来的内容将详细阐述基于存储证明的比特币挖矿行为的细节。让我们先从存储证明说起吧。
存储证明(Proof of storage)
你认为当前基于工作量证明的比特币挖矿行为浪费了宝贵的电力,好吧,我也这么认为,虽然这种行为并不比传统的银行更浪费资源。然而,却有办法让这种浪费更有意义,比如本文将要说的,矿工们必须分布式存储一个有意义且重要的大文件,才能实施挖矿行为,换句话说,不是随便一个矿工就可以肆意浪费电能赚钱的,你必须参与分布式存储。
这样在挖矿设备的投资便可以用于大规模分布式存储,这是一件好事。
那么,需要做的仅仅就是,在挖矿过程中证明自己确实帮忙存储了文件,至于如何做到这一点,这正是Proof of storage(存储证明)的细节。
Proof of storage挖矿过程实例
让我们从最简单的开始。
假设有一个大文件 F F ,比如它是人类几千年的历史档案,这个文件显然相当大,但非常有意义,任何一个单独的个人都无法保存整个这一个文件,那么最简单的做法就是把文件切割,存到Hadoop HDFS里面去,但是我们不想这么做,我们希望去中心化地存储。当然,可以按照本文前面讲的那种方法分布式存储到全球,同时支付费用,这显然是可行的。但是本文描述的方法是,它可以和比特币挖矿行为结合起来玩,这样既可以让那些暴发户矿工付出点良心上的代价,又可以满足分布式存储的需求,妙哉,妙哉啊!
首先,规定三个数, N N , k1 k 1 和 k2 k 2 ,其中:
- N N 的意义:表示该大文件被分割成了多少块,显然这是一个很大的数字。
- k1 k 1 的意义:表示每一个节点(即矿工)必须保存文件 F F 的文件子块数。
- k2 k 2 的意义:表示每一个节点(即矿工)在挖矿成功后必须上报的存储证明文件子块数。
示意图如下所示:
此外,每一个节点具体保存那些子块是由其公钥决定的,而公钥是不会重复的,因此概率上看,即可实现任意的文件子块均匀地被存储在任意的节点中。
让我们直接开始算法的过程:
∀i∈{1,2,3...k1}设: ∀ i ∈ { 1 , 2 , 3... k 1 } 设 :
m[i]=H(Kpub||i)modN m [ i ] = H ( K p u b | | i ) mod N
此时,所有的 m[i] m [ i ] 便形成了一个集合,我们把这个集合设为 Gm G m :
Gm={m[0],m[1],m[2],...m[k1]} G m = { m [ 0 ] , m [ 1 ] , m [ 2 ] , . . . m [ k 1 ] }
该集合其实是一个文件 F F 的子块的索引集合,它指示了公钥 Kpub K p u b 所有者节点需要存储文件 F F 的哪几个子块,该节点我们设为节点 NK N K 。我们注意到,每一个节点具体存储哪几个子块,是由该节点的公钥决定的,每一个节点显然都有一个公钥,用来生成比特币钱包然后接收挖矿奖励的比特币。
由上面的设定,我们知道,节点 NK N K 需要存储的文件子块为:
GF={(F[i],πi)|i∈Gm} G F = { ( F [ i ] , π i ) | i ∈ G m }
其中 πi π i 为文件子块 F[i] F [ i ] 的哈希值,处于一棵Merkle树的叶子位置,用于证明自己真的拥有正确的文件子块 F[i] F [ i ] ,毕竟如果用错误的数据代替,块的哈希值将无法通过Merkle树的验证。
接下来,花式技巧要来了。这里将是关键。
基于存储证明的谜题,虽然要求矿工至少存储 k1 k 1 个文件子块,但是却不是每次必须把拥有这 k1 k 1 个子块的证明出示给验证者,这是为了效率考虑,毕竟现实中 k1 k 1 的值可能会非常大,全部出示存储证据效率会很低,所以基于Proof of storage的挖矿机制可以只要矿工能出示这 k1 k 1 个文件子块里面随机的稍微小一些的 k2 k 2 个存储证明就行了,显然这里 k1>k2 k 1 > k 2 。
理论上,只要 k2 k 2 个随机数足够随机,即均匀分布在 k1 k 1 个索引之间,矿工就必须不得不保存所有的 k1 k 1 个文件子块,毕竟它并不知道这里面的哪几个子块需要证明为其所存储,在概率上,每一个子块均有同等的可能被要求存储证明。
那么,要如何选择 k2 k 2 个存储证据呢?显然,这里面必须引入随机且无法预测的因素。区块链最后一个区块的哈希值便是一个很好的随机源。
设当前区块链最后一个区块的哈希值为 Z Z ,这里的 Z Z 随着区块链的延展在不断发生变化,谁也无法预知它的变化趋势,接下来的事情和标准比特币的挖矿行为完全一致,即找出一个 s s 值,满足去块头里面的难度需求即可,然而当这个 s s 值被找出来后,挖矿并没有像比准比特币系统里那样结束!矿工除了出示 s s 值之外,还必须按照以下的规则出示 k2 k 2 个文件子块的存储证明:
∀i∈{1,2,3...k2}设: ∀ i ∈ { 1 , 2 , 3... k 2 } 设 :
n[i]=m[H(Kpub||Z||i||s)modk1] n [ i ] = m [ H ( K p u b | | Z | | i | | s ) mod k 1 ]
所有的 n[i] n [ i ] 便形成了另一个集合(注意和第一个集合 Gm G m 的区别和联系),显然它是 Gm G m 的真子集(因为 k1>k2 k 1 > k 2 ),我们把这个集合设为 Gn G n :
Gn={n[0],n[1],n[2],...n[k2]} G n = { n [ 0 ] , n [ 1 ] , n [ 2 ] , . . . n [ k 2 ] }
最后矿工交付下面的ticket供校验者查验即可:
ticket=(Kpub,s,{F[i],πi}∀i∈Gn) t i c k e t = ( K p u b , s , { F [ i ] , π i } ∀ i ∈ G n )
ticket是矿工挖矿的最终交付件,将接收大众的检验。
Proof of Storage校验过程
校验过程非常简单,检验者收到矿工的 ticket t i c k e t 后,除了像标准比特币系统计算区块的哈希后和难度值比较外,还会根据其提供的 Kpub K p u b , s s 以及形成共识的 Z Z , k2 k 2 ,来生成集合 G′n G n ′ ,如果:
G′n=Gn G n ′ = G n ( Gn G n 包含在 ticket t i c k e t 中)
那么校验者会根据 ticket t i c k e t 中的 {F[i],πi}∀i∈Gn { F [ i ] , π i } ∀ i ∈ G n 中提供的文件子块索引以及 πi π i 来校验Merkle树,一直校验到树的root。
显然,如果矿工并没有存储文件子块,那么它将不会拥有正确的 πi π i (文件子块 F[i] F [ i ] 的哈希值)的值,Merkle树校验将会失败!
总结和问题
我们来总结一下。
和标准的比特币挖矿不同,基于存储证明的挖矿行为在标准的基于工作量证明之外,还必须提供它确实存储了指定的文件子块这样的证据。如此一来,虽然不可避免地也是消耗了大量的电能,但是至少矿工做了一件不得已的善事,即“为了挖矿赚比币,它必须帮忙存储一个有意义的文件的一部分,否则,它便无法挖矿”
可见,这是被逼的!
被逼的矿工一定会想办法做坏事。
通篇整个过程看来,我们发现其实根本就不用存储实际的 F[i] F [ i ] ,而只要存储 F[i] F [ i ] 的哈希值即可,因为整个过程中用到 F[i] F [ i ] 地方就只有最后校验Merkle树的过程。因此矿工可以做以下两件事:
- 第一次挖矿前按照规矩老老实实下载根据自己公钥生成的 Gm G m 指定索引的文件子块,然后为每一个子块计算哈希值后把这些子块删除。
- 伙同多个矿工一起交换子块的哈希值后所有节点均可以永久删除存储的子块,这种事是利好团伙的,虽然在挖矿行为上它们是竞争关系,但在拒绝存储子块这件事上,它们有着共同的利益。
鉴于这个教训,我们可以总结出两点:
- 每一个矿工要存储的文件子块集合要根据各个矿工自己密钥生成,保证足够的均匀性,保证一个大文件均匀地被存储在各个矿工那里
- 必须有一种措施保证每一个矿工节点确实在本地存储了文件子块集合,而不是仅仅存一个哈希集合来欺骗
为此,必须将文件子块 F[i] F [ i ] 本身加入到引入随机因素的哈希计算中!所以上述的Proof of storage挖矿行为只是理想中的行为,只是为了帮助理解整个过程而已,真正的Permacoin所使用的方法与此并不相同。
且见下文分解
Permacoin的做法
解决作弊行为的措施貌似非常简单,但是在涉及到信息安全(这里强调完整性以及不可抵赖性)的领域,有一个原则,那就是“不要自己发明算法和协议,要使用经过考验的胜出机制”,所以这里就不再有更多的臆想了,直接上Permacoin的Paper上的做法。
和理想中的Proof of storage不同,Permacoin自带了防作弊的手法!不同点体现在集合 Gn G n 的生成上。
为了体现差异,我再把理想中的 Gn G n 生成的算法展示一遍:
∀i∈{1,2,3...k2}设: ∀ i ∈ { 1 , 2 , 3... k 2 } 设 :
n[i]=m[H(Kpub||Z||i||s)modk1] n [ i ] = m [ H ( K p u b | | Z | | i | | s ) mod k 1 ]
Permacoin的 Gn G n 生成算法与此不同,它是这么生成的:
σ0=0 σ 0 = 0
n1=m[H(Kpub||Z||s)modk1] n 1 = m [ H ( K p u b | | Z | | s ) mod k 1 ]
For F o r i=1,2,...k2 i = 1 , 2 , . . . k 2
Do: D o :
hi=H(Kpub||Z||σi−1||F[ni]) h i = H ( K p u b | | Z | | σ i − 1 | | F [ n i ] ) (这里是关键,将 F[ni] F [ n i ] 本身引入)
σi=signKpriv(hi) σ i = s i g n K p r i v ( h i )
ni+1=H(Kpub||Z||σi)modk2 n i + 1 = H ( K p u b | | Z | | σ i ) mod k 2
Done D o n e
以上的做法几乎封闭了所有的作弊通道。你想作个弊试试?
关于作弊和51攻击
很多人忽略了社会工程学,很多人忽略了博弈论,以为比特币以及各种另类币所代表的金融行为只能用技术来解释,这是大错特错。
技术上,如果有人或者团体掌握了51%以上的算力,就有能力发动攻击。但在现实中,真的会有人这么做吗?他发动攻击的目的是什么?他把比特币系统攻破了,能得到美元或者黄金吗?请注意,攻击者根本就没有任何动机从内部瓦解比特币系统。
发动51攻击造成的后果是使得区块链恶意分叉,从而完成一笔或者几笔双重支付,然而请注意,如果你仅仅为了一双皮鞋而发动这样的攻击是完全没有意义的,但是如果你针对全球的皮鞋行业发动了一个针对大额比特币双重支付的攻击,其后果便是人们对比特币系统丧失信心,这足以让比特币大幅贬值甚至市场崩溃,这相当于攻击者在万米高空肢解了自己乘坐的飞机,请问他能得到什么好处,难道是永恒?
51攻击就好比说,如果有人掌握了XX,就可以支配银行一样,但是除了极少数国家,银行并非那么危险,所有人的共识造成了银行即便在战争中都是安全的,虽然抢劫银行的事情时有发生,但依然是小概率事件,并且涉案金额都很小。危险性并不在比特币系统本身,而在之外。比如利用了比特币匿名性的勒索病毒就是如此。
在一个系统中,在分析坏事的时候,一定要考虑做这种事的动机,比特币的攻击行为并不像软件漏洞或者病毒那样,后者一旦把原理释放,所谓的脚本小子都能造成严重的后果,但是比特币系统完全不同,这是一个金融博弈系统,自带负反馈机制,这种负反馈完全可以抵消攻击者的攻击行为带来的收益,因此他并没有什么动机去发动攻击。
3个月回归!
跋
本周心力交瘁,感觉到了压力。
谈笑没鸿儒,往来全白丁,
不会调素琴,也看不懂经,
…
黄鹤之飞尚不得过,怒而飞,其翼若垂天之云…
魂飞苦,摧心肝,愁空山,
一桥飞架南北,天堑变通途。
参考资料
Permacoin: Repurposing Bitcoin Work for Data Preservation:http://soc1024.ece.illinois.edu/permacoin.pdf