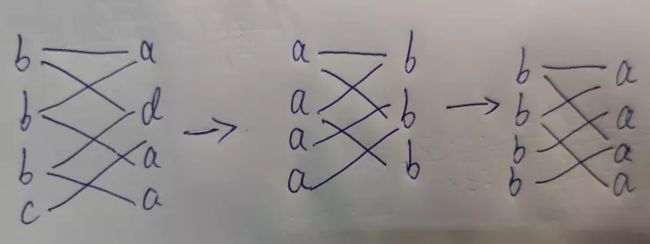标签传播算法（Label Propagation Algorithm, LPA）初探

0. 社区划分简介

0x1：非重叠社区划分方法

在一个网络里面，每一个样本只能是属于一个社区的，那么这样的问题就称为非重叠社区划分。

在非重叠社区划分算法里面，有很多的方法：

1. 基于模块度优化的社区划分

基本思想是将社区划分问题转换成了模块度函数的优化，而模块度是对社区划分算法结果的一个很重要的衡量标准。

模块度函数在实际求解中无法直接计算得到全局最优解析解（类似深度神经网络对应的复杂高维非线性函数），所以通常是采用近似解法，根据求解方法不同可以分为以下几种方法：

1. 凝聚方法(down to top): 通过不断合并不同社区，实现对整个网络的社区划分，典型的方法有Newman快速算法，CNM算法和MSG-MV算法；
2. 分裂方法(top to down): 通过不断的删除网络的边来实现对整个网络的社区划分，典型的方法有GN算法；
3. 直接近似求解模块度函数(近似等价解): 通过优化算法直接对模块度函数进行求解，典型的方法有EO算法；

2. 基于谱分析的社区划分算法
3. 基于信息论的社区划分算法
4. 基于标签传播的社区划分算法

undone

Relevant Link:

https://www.cnblogs.com/LittleHann/p/9078909.html

 

1. Label Propagation简介

LPA是一种基于标签传播的局部社区划分。对于网络中的每一个节点，在初始阶段，Label Propagation算法对于每一个节点都会初始化一个唯一的一个标签。每一次迭代都会根据与自己相连的节点所属的标签改变自己的标签，更改的原则是选择与其相连的节点中所属标签最多的社区标签为自己的社区标签，这就是标签传播的含义了。随着社区标签不断传播。最终，连接紧密的节点将有共同的标签。

0x1：LPA基本思想

LPA认为每个结点的标签应该和其大多数邻居的标签相同，将一个节点的邻居节点的标签中数量最多的标签作为该节点自身的标签（bagging思想）。给每个节点添加标签（label）以代表它所属的社区，并通过标签的“传播”形成同一个“社区”内部拥有同一个“标签”。

笔者思考：

在基本思想上，LPA 和 Kmean 本质非常类似，在 LPA 的每轮迭代中，节点被归属于哪个社区，取决于其邻居中累加权重最大的label（取数量最多的节点列表对应的label是weight=1时的一种特例），而 Kmeans的则是计算和当前节点“最近”的社区，将该节点归入哪个社区。
但是这两个算法还是有细微的区别的:

1. 首先: Kmeans是基于欧式空间计算节点向量间的距离的，而LPA则是根据节点间的“共有关系”以及“共有关系的强弱程度”来度量度量节点间的距离；
2. 第二点: Kmeasn中节点处在欧式空间中，它假设所有节点之间都存在“一定的关系”，不同的距离体现了关系的强弱。但是 LPA 中节点间只有满足“某种共有关系”时，才存在节点间的边，没有共有关系的节点是完全隔断的，计算邻居节点的时候也不会计算整个图结构，而是仅仅计算和该节点有边连接的节点，从这个角度看，LPA 的这个图结构具有更强的社区型；

0x2：LPA算法优点

LPA算法的最大的优点就是算法的逻辑非常简单，相对于优化模块度算法的过程是非常快的，不用pylouvain那样的多次迭代优化过程。

LPA算法利用自身的网络的结构指导标签传播，这个过程是无需任何的任何的优化函数，而且算法初始化之前是不需要知道社区的个数的，随着算法迭代最后可以自己知道最终有多少个社区。

 

笔者思考： 其实 LPA 之所以可以做到无需开发者指定聚类的社区个数，核心原因是因为 LPA 是一个彻底的 down to top 聚类算法，其实如果对 Kmeans 稍加改造，将其初始化过程改为将所有节点都初始化为单独的cluster，然后也进行 down to top 的聚类，Kmeasn也可以做到无需显式指定cluster数量。

0x3：LPA算法缺点

划分结果不稳定，随机性强是这个算法致命的缺点。具体体现在：

1. 更新顺序：节点标签更新顺序随机，但是很明显，越重要的节点越早更新会加速收敛过程；
2. 随机选择：如果一个节点的出现次数最大的邻居标签不止一个时，随机选择一个标签作为自己标签。这种随机性可能会带来一个雪崩效应，即刚开始一个小小的聚类错误会不断被放大。不过话也说话来，如果相似邻居节点出现多个，可能是weight计算的逻辑有问题，需要回过头去优化weight抽象和计算逻辑；

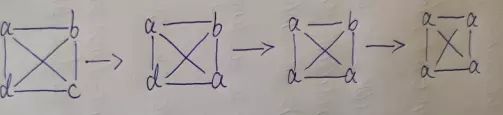
0x4：LPA的一个简单例子

算法初始化：a、b、c、d各自为独立的社区；

第一轮标签传播：

一开始c选择了a，因为大家的社区标签都是一样的，所以随机选择了一个；

d也根据自己周围的邻居节点来确定标签数，最多的是a，所以就是d为a了；

继续标签传播：以此类推，最后就全部都是a了；

Relevant Link:

https://www.jianshu.com/p/cff65d7595f9
https://arxiv.org/pdf/0709.2938.pdf
https://blog.csdn.net/Katherine_hsr/article/details/82343647
http://sighingnow.github.io/%E7%A4%BE%E4%BC%9A%E7%BD%91%E7%BB%9C/community_detection_k_means_clustering.html

 

2. LPA算法过程

0x1：算法过程描述

第一步：先给每个节点分配对应标签，即节点1对应标签1，节点i对应标签i； 
第二步：遍历N个节点（for i=1：N），找到对应节点邻居，获取此节点邻居标签，找到出现次数最大标签，若出现次数最多标签不止一个，则随机选择一个标签替换成此节点标签；
第三步：若本轮标签重标记后，节点标签不再变化（或者达到设定的最大迭代次数），则迭代停止，否则重复第二步   

0x2：边权重计算

社区图结构中边的权重代表了这两个节点之间的的“关系强弱”，这个关系的定义取决于具体的场景，例如：

1. 两个DNS域名共享的client ip数量；
2. 两个微博ID的共同好友数量；

0x3：标签传播方式

LPA标签传播分为两种传播方式，同步更新，异步更新。

1. 同步更新

同步的意思是实时，即时的意思，每个节点label更新后立即生效，其他节点在统计最近邻社区的时候，永远取的是当前图结构中的最新值。

对于节点，在第 t 轮迭代时，根据其所在节点在第t-1代的标签进行更新。也就是

，其中表示的就是节点在第 t 次迭代时的社区标签。

函数表示的就是取参数节点中社区标签最多的。

需要注意的是，这种同步更新的方法会存在一个问题，当遇到二分图的时候，会出现标签震荡，如下图：

这种情况和深度学习中SGD在优化到全局最优点附近时会围绕最优点附近进行布朗运动（震荡）的原理类似。解决的方法就是设置最大迭代次数，提前停止迭代。

2. 异步更新

异步更新方式可以理解为取了一个当前社区的快照信息，基于上一轮迭代的快照信息来进行本轮的标签更新。

0x4： 算法代码

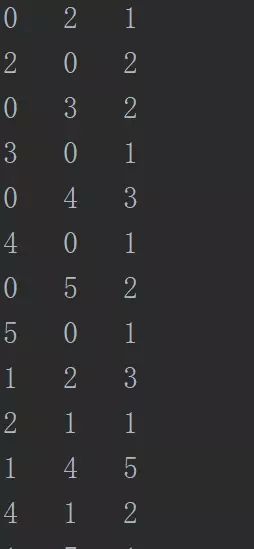
1. 数据集

3列分别是：【node_out，node_in，edge_weitght】

2. 社区初始化

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import string

def loadData(filePath):
    f = open(filePath)
    vector_dict = {}
    edge_dict = {}
    for line in f.readlines():
        lines = line.strip().split("   ")
        for i in range(2):
            if lines[i] not in vector_dict:
                vector_dict[lines[i]] = int(lines[i])
                edge_list = []
                if len(lines) == 3:
                    edge_list.append(lines[1 - i] + ":" + lines[2])
                else:
                    edge_list.append(lines[1 - i] + ":" + "1")
                edge_dict[lines[i]] = edge_list
            else:
                edge_list = edge_dict[lines[i]]
                if len(lines) == 3:
                    edge_list.append(lines[1 - i] + ":" + lines[2])
                else:
                    edge_list.append(lines[1 - i] + ":" + "1")
                edge_dict[lines[i]] = edge_list
    return vector_dict, edge_dict

if __name__ == '__main__':
    filePath = './label_data.txt'
    vector, edge = loadData(filePath)
    print(vector)
    print(edge)

初始化时，所有节点都是一个独立的社区。

3. LPA社区聚类迭代

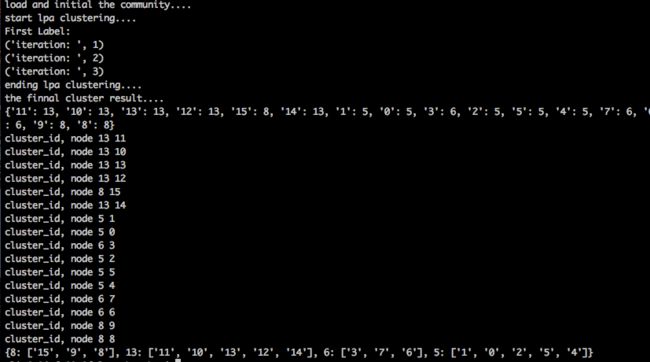
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import string


def loadData(filePath):
    f = open(filePath)
    vector_dict = {}
    edge_dict = {}
    for line in f.readlines():
        lines = line.strip().split("   ")
        for i in range(2):
            if lines[i] not in vector_dict:
                vector_dict[lines[i]] = int(lines[i])
                edge_list = []
                if len(lines) == 3:
                    edge_list.append(lines[1 - i] + ":" + lines[2])
                else:
                    edge_list.append(lines[1 - i] + ":" + "1")
                edge_dict[lines[i]] = edge_list
            else:
                edge_list = edge_dict[lines[i]]
                if len(lines) == 3:
                    edge_list.append(lines[1 - i] + ":" + lines[2])
                else:
                    edge_list.append(lines[1 - i] + ":" + "1")
                edge_dict[lines[i]] = edge_list
    return vector_dict, edge_dict


def get_max_community_label(vector_dict, adjacency_node_list):
    label_dict = {}
    for node in adjacency_node_list:
        node_id_weight = node.strip().split(":")
        node_id = node_id_weight[0]
        node_weight = int(node_id_weight[1])

        # 按照label为group维度，统计每个label的weight累加和
        if vector_dict[node_id] not in label_dict:
            label_dict[vector_dict[node_id]] = node_weight
        else:
            label_dict[vector_dict[node_id]] += node_weight

    sort_list = sorted(label_dict.items(), key=lambda d: d[1], reverse=True)
    return sort_list[0][0]


def check(vector_dict, edge_dict):
    for node in vector_dict.keys():
        adjacency_node_list = edge_dict[node]   # 获取该节点的邻居节点
        node_label = vector_dict[node]          # 获取该节点当前label
        label = get_max_community_label(vector_dict, adjacency_node_list)   # 从邻居节点列表中选择weight累加和最大的label
        if node_label >= label:
            continue
        else:
            return 0    #  找到weight权重累加和更大的label
    return 1


def label_propagation(vector_dict, edge_dict):
    t = 0
    print('First Label: ')
    while True:
        if (check(vector_dict, edge_dict) == 0):
            t = t + 1
            print('iteration: ', t)
            # 每轮迭代都更新一遍所有节点的社区label
            for node in vector_dict.keys():     
                adjacency_node_list = edge_dict[node]
                vector_dict[node] = get_max_community_label(vector_dict, adjacency_node_list)
        else:
            break
    return vector_dict



if __name__ == '__main__':
    filePath = './label_data.txt'
    vector, edge = loadData(filePath)
    print "load and initial the community...."
    #print(vector)
    #print(edge)
    print "start lpa clustering...."
    vector_dict = label_propagation(vector, edge)
    print "ending lpa clustering...."
    print "the finnal cluster result...."
    print(vector_dict)

    cluster_group = dict()
    for node in vector_dict.keys():
        cluster_id = vector_dict[node]
        print "cluster_id, node", cluster_id, node
        if cluster_id not in cluster_group.keys():
            cluster_group[cluster_id] = [node]
        else:
            cluster_group[cluster_id].append(node)
    

    print cluster_group

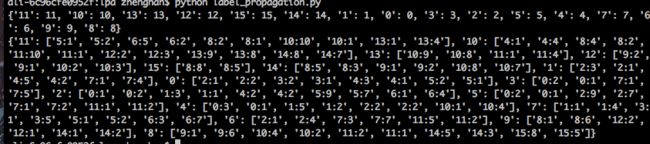
最后得到的聚类社区为：

{8: ['15', '9', '8'], 13: ['11', '10', '13', '12', '14'], 6: ['3', '7', '6'], 5: ['1', '0', '2', '5', '4']}

Relevant Link: 

https://github.com/GreenArrow2017/MachineLearning/tree/master/MachineLearning/Label%20Propagation
https://www.jianshu.com/p/cff65d7595f9

 

3. LPA算法改进思路

0x1：标签随机选择改进

给节点或边添加权重（势函数、模块密度优化、LeaderRank值、局部拓扑信息的相似度、标签从属系数等），信息熵等描述节点的传播优先度。

这样，在进行邻居节点的最大标签统计的时候，可以将邻居节点的weight权值等作为参考因素。

0x2：标签初始化改进

可以提取一些较为紧密的子结构来作为标签传播的初始标签（例如非重叠最小极大团提取算法），或通过初始社区划分算法先确定社区的雏形再进行传播。  

Relevant Link:

https://www.cnblogs.com/bethansy/p/6953625.html
https://blog.csdn.net/zzz24512653/article/details/26151669