[译]背景:着色的物理和数学(1)
[译]背景:着色的物理和数学(1)
(译者注:本文是翻译的Naty Hoffman的《Background: Physics and Math of Shading》。我希望通过翻译此文,彻底理解PBR的原理。某些我实在不知道如何恰当翻译的地方,就把英文原文也放上了。原文太长,因此分几部分依次放上来。)
在本课堂讲义中,我们将复习基于物理的渲染(Physically Based Rendering)模型的基础。首先,定性地描述PBR的物理学基础。然后,定量地描述PBR的数学模型。最后,探讨如何将这些数学模型实现为着色代码。
着色的物理学
着色描述的是光与物相互作用的那些物理现象。为了理解这些现象,就需要理解一点光的本质。
光是一种横向电磁波,意思是,它的振动方向与它的传播方向是垂直的(见Figure 1)。既然是波,光就由其波长——从波峰到波峰的距离表征。电磁波波长覆盖的范围很广,但是只有一小部分(大约400-700纳米)才对人可见,因此对着色有意义(见Figure 2)。
与光相关的一个属性叫做折射率。折射率是个复数:它的实部度量物质如何影响光速(相对真空中的速度降低;它的虚部度量光在传播过程中是否被吸收(转换为其他形式的能量)。折射率是光的波长的函数。
(译者注:参考 https://baike.baidu.com/item/复折射率)
均匀介质
光-物交互的最简单情形就是光通过均匀介质传播。这样的介质的折射率是处处相同的(在光波长的数量级上;在讨论可见光时,这指的是任何远小于100纳米的变量都忽略不计)。
所谓透明的介质,就是其折射率的复数部分对可见光波长来说很小。这意味着没有明显的吸收作用,任何穿过介质的光直接沿直线穿行,没有改变方向。透明介质的例子包括水和玻璃(见Figure 3)。
(译者注:这里的“没有改变方向”,是指光在水中和玻璃中穿梭时没有改变方向,不是说光在两种介质之间时不改变方向。)
如果一种均匀介质确实对可见光发生了明显的吸收作用,它会吸收一定量的经过它的光。光传输的距离越远,吸收的就越多。但是,光的方向不会改变,只有强度改变了(而且,如果吸收对某种可见波长是选择性的,光的颜色也会改变)——见Figure 4。
注意,介质的规模和吸收能力一样很重要。例如,水实际上是吸收了一点点可见光的,特别是光谱的红色端。在几英尺范围内这是微不足道的(如Figure 3所示),但是在很远的距离上看就相当明显了——见Figure 5。
散射
在均匀介质中,光总是沿直线传播,不改变方向(尽管它的强度会因吸收而减弱)。不均匀介质的折射率是各处不同的。如果折射率缓慢而连续地变化,那么光会弯曲成曲线。然而,如果折射率突然地改变(比如在比光的波长更短的距离上改变),那么光就会发生散射:它被拆分到多个方向上。注意,散射没有改变光的总的强度。
微观粒子引入了孤立的“岛”的概念,在它周围的折射率是各不相同的。这导致光不断地转换散射方向(见Figure 6)。注意,散射开的光在不同方向上的分布是不均匀的,具体情况由粒子的类型决定。有的导致向前散射(大部分光向前),有的导致向后散射(大部分光反向),有的则导致复杂的分布(在某些方向上分布很多)。
在雾状介质上,散射现象比较强烈,这使得光的传播方向随机化(Figure 7)。在半透明或不透明介质上,散射现象特别强烈,这使得光的传播方向完全随机了(Figure 8)。
与吸收类似,散射效果也受规模的影响。例如,清洁的空气在很近的距离内的散射效果微乎其微,在很远的距离上则会引起很大的散射效果(Figure 9)。
介质的外观(Media Appearance)
前面的章节介绍了光与物交互的两种模式。折射率的复数部分不为零的介质会吸收光线,光的强度会随着传输距离的增加而减少(如果只吸收特定波长,可能还会改变光的颜色),但光的方向不变。另一方面,急速变化的折射率会引起散射——光的方向改变(被拆分为多个方向上的光),但光的总能量或光谱分布不变。还有第三种交互模式:自发光,即从其他形式的能量转换为光(与吸收相反)。这是光源的情况,但在研究着色时不常见。Figure 10展示了这三种交互方式。
大多数介质都有一定程度的散射和吸收光。每种介质的外观都由散射和吸收的相对量决定。Figure 11展示了多种散射和吸收组合的介质的情况。
平面边界处的散射
麦克斯韦方程可以用于计算折射率改变时光的行为,但是大多数时候不存在解析解。有一个特殊情况有解,而且它和表面着色关系密切。这就是两个不同折射率的介质之间的无限大的完美的平面边界。这很好地描述了物体的边界的情况:一边是空气的折射率,一边是其他物体的折射率。麦克斯韦方程在此情形下的方案被称为菲涅耳方程(Fresnel Equations)。
虽然真实物体的表面不是无限大,但是与可见光的波长相比,它们可以被认为是无限大的。至于“完美地平”,会有人反驳说没有什么物体的表面是真的平的——不说别的,原子们就会形成兆分之一小的“凹凸”。但是,与其他事情一样,与光波长相近的数量级才有研究意义。实际上制作100纳米数量级上的完美平面是可以做到的——这种表面被称为光学平面,通常被用于制作高质量光学仪器,比如望远镜。
在此特殊情形下,光不是在所有方向发生散射,而是分为了2个方向:反射和折射(Figure 12)。
如你可在Figure 12中所见的,反射角等于入射角,但是折射角不同,它依赖于介质的折射率(如果你对严格的数学公式感兴趣,就查一下Snell法则)。反射光和折射光的比例可以用菲涅耳方程描述,我们将在后续章节详细讨论之。
非光学平面的表面
当然,大多数现实世界的表面没有被打磨到望远镜镜片那样的光滑。达不到光学平面的表面上,会发生什么?大多数情形下,都会有这样的不规则表面:它们的远大于光波长,但远小于可见或可渲染的尺度(就是说,它们比着色采样的一个像素还要小)。此时,表面就像是由大量的极小的光学平面组成的。表面的最终表现,就是很多不同朝向的小平面的表现的集合——每个小平面的朝向都略有不同(Figure 13)。
在微观水平上,表面越粗糙,反射就越模糊,这是因为构成表面的小平面的朝向就比表面的的总朝向偏离得越严重(Figure 14)。从着色的角度,通常可以用统计学的方式处理这些微几何形态,并将表面视为从一个点上可以朝多个方向反射(和折射)光线(Figure 15)。
下表面散射
(译者注:subsurface,也被译为次表面、子表面等,理解含义即可。)
折射光后来怎么样了?这由物体的构成决定。对于金属,折射光立即被吸收了(金属对可见光的吸收系数(折射率的虚部)很高)——能量立即被自由电子吸收了。另一方面,非金属(电介质、绝缘体)的表现就很常规。光被折射进入后,非金属就展现出我们前面章节讨论的吸收和散射行为。大多数情况下,一部分折射光在被充分散射后会重新离开表面。总之,如Figure 16所示。
在Figure 16右侧,你可以看到下表面散射光(用蓝色箭头表示)从表面的多处离开了,离开点与入射点距离各不相同。Figure 17展示了这些距离与像素的关系的两种情形。在左上方,像素大于进-出下表面散射距离。此时,进-出距离可以忽略,下表面散射光可以被视为由入射点出来的,就像右上方描述的那样。此时着色完全可以在局部的片段着色器中解决:某点的输出光仅依赖于此点的入射光。在Figure 17下方,像素小于进-出距离。此时,一个点的着色要收到其他点的光的影响。为适应这一情形,局部的片段着色器就不适用了,必须使用其他的专门的渲染技术。这被称为“下表面散射”技术,但重点是,普通的散射着色方案也是对同一物理现象(折射光的下表面散射)的结果。唯一的区别就是在观察数量级(单个像素尺寸的数量级)上散射距离的大小。这个深刻的结论告诉我们,在距离摄像机比较远的时候(例如远距离的角色的皮肤),那些展现出“下表面散射”行为的材质,也可以被常规的散射着色方法处理。另一方面,在距离摄像机很近的时候(例如十分接近一个塑料玩具),那些展现出“常规散射”行为的材质,会出现“下表面散射”的现象。
着色的数学
测量一般的电磁辐射(radiation)(包括可见光)的学问被称为辐射测量学(radiometry)。有很多种测量光的物理量,我们只关心一种:辐射率(radiance),用于度量一个单独的光线的强度。我们用通用的辐射度量符号L表示辐射率;当对一个表面上的点着色时,Li表示入射光的辐射率,Lo表示出射光的辐射率。
辐射率(和其他辐射度量学物理量一样)是一个光谱量:它是波长的函数。理论上,为表示可见光的辐射率,需要存储一个连续的光谱分布图。某些特制的渲染应用程序中确实使用了密集的光谱采样。但在生产渲染(电影和游戏)中,存储的是RGB三元组。很多教程(包括Read-Time Rendering)都介绍了三元组与光谱分布的关系。
BRDF
如Figure 17右上方所示,一般都假设着色可以在局部(一个单独的片段内)处理。此时,一个给定的表面上的某点如何反光,这仅取决于入射光和出射光(观察者)方向。本文中,我们用v表示单位长度的向量,其指向出射光方向,用l表示单位长度的向量,其指向入射光的反方向(让所有向量都背向表面,会比较方便)。表面对光的反射情况用BRDF函数(双向反射分布函数Bidirectional Reflectance Distribution Function)量化描述,我们用f(l, v)表示它。每个方向都可以用两个数值(例如极坐标)参数化表示,所以BRDF的总的维度是4。很多情况下,围绕着表面的法线旋转入射光和观察者,不会影响BRDF的输出结果。这样各向同性的BRDF函数可以用3个角度做参数,如Figure 18所示。在实际应用中,一个BRDF使用的角度数量从1到5不等;一些常用的角度如Figure 19所示。
原则上,BRDF函数只对在表面上方的入射光和观察者有定义(穿透表面用BTDF函数建模,BSDF函数则同时包含反射和穿透);换句话说,点积nl和nv(在BRDF函数中很常见)必须都是非负数。避免背面入射光很简单:只收集正面方向上的入射光,或者将背面的入射光的贡献值设置为0。背面的观察者理论上永远不会出现,但是插值的顶点法线和法线映射(游戏中常见的技术)可能创造出这样的情况。nv为负数时的BRDF的求值可以避免(将nv裁切为0或使用其绝对值)。某些时候,直接使用nv为负数时的BRDF的值可能产生更好的结果,但必须对数学计算十分谨慎。
BRDF函数可以直观地用两种方式解读,都是有效的。一种是,给定一束来自某个方向的入射光,BRDF可以算出在表面上所有方向上的出射光线的反射和散射的相对分布情况。另一种是,给定一个观察者的方向,BRDF可以算出对此出射方向有贡献的所有入射光的相对分布情况。这两种解读如Figure 20所示。
BRDF函数是一个光谱量。理论上,额外加入输入和输出光的波长,会极大增加它的维度。但是,实际应用中两个不同的波长不会相互干扰(荧光和磷光现象会有这种干扰,不过它们极少用在着色产品上),所以出射光的波长只会受相同波长的入射光的影响。这意味着,我们不必将入射和出射波长当作BRDF的参数,我们只需将BRDF当作一个乘以光谱值(颜色值)的函数。在着色产品中,这指的就是乘以RGB颜色值的BRDF函数。
BRDF被用于反射率方程(reflectance equation):
尽管这个方程看起来很吓人,它的含义确很简单:输出光的辐射率等于(BRDF乘以入射光辐射率乘以cos因子)在(表面上所有方向)上的积分。如果你不熟悉积分,你可以把它看作是连续的加权平均。(译者注:这个解释反而让我糊涂,幸好我知道什么是积分)方程中的⊗符号用于表示各个元素分别进行的向量乘法,用到它是因为BRDF和光颜色都是RGB向量。
注意,任何一个接收入射光返回出射光的函数都可以自称为BRDF函数。一个物理上正确的BRDF函数应该满足两个条件:可交换性和能量守恒。
可交换性意思是交换l和v后BRDF的输出不变,即
能量守恒是指表面反射的光总能量不能超过入射光的总能量。数学上用下述不等式描述:
这意味着,对任何可能的入射光l,(BRDF乘以出射方向v乘以cos因子)的积分不能超过1。
BRDF函数描述的至少有两种现象(对非金属):表面反射和下表面散射。不同的现象有不同的行为,BRDF一般对每个现象都有专门的部分。BRDF中描述表面反射的部分被称为specular项,描述下表面散射的部分被称为diffuse项——见Figure 21。
表面反射(Specular项)
未完待续。。
![[译]背景:着色的物理和数学(1)_第1张图片](http://img.e-com-net.com/image/info8/2e6362f3560d4ebbae925d89ec249c6d.jpg)
![[译]背景:着色的物理和数学(1)_第2张图片](http://img.e-com-net.com/image/info8/8a718c372bc64231b007e3e594cc7108.jpg)
![[译]背景:着色的物理和数学(1)_第3张图片](http://img.e-com-net.com/image/info8/b762cb0467094c36886108173a0a24c2.jpg)
![[译]背景:着色的物理和数学(1)_第4张图片](http://img.e-com-net.com/image/info8/b45c1b49820d406e895909cc7427af66.jpg)
![[译]背景:着色的物理和数学(1)_第5张图片](http://img.e-com-net.com/image/info8/1b825e92ba2d4405a461cb85c7185edd.jpg)
![[译]背景:着色的物理和数学(1)_第6张图片](http://img.e-com-net.com/image/info8/e782817399d5443989dfc170fc923a21.jpg)
![[译]背景:着色的物理和数学(1)_第7张图片](http://img.e-com-net.com/image/info8/9d285c5be43346cf81965f8b9dbbea08.jpg)
![[译]背景:着色的物理和数学(1)_第8张图片](http://img.e-com-net.com/image/info8/2834d3c2787540cc83fb07e19e590ca9.jpg)
![[译]背景:着色的物理和数学(1)_第9张图片](http://img.e-com-net.com/image/info8/46cc20109daa4bc991a8ae98fbf6dc92.jpg)
![[译]背景:着色的物理和数学(1)_第10张图片](http://img.e-com-net.com/image/info8/d2f1aadc75724216b18fdd8934be5bb7.jpg)
![[译]背景:着色的物理和数学(1)_第11张图片](http://img.e-com-net.com/image/info8/be8d3638ddfd4ed097653e0760d3791b.jpg)
![[译]背景:着色的物理和数学(1)_第12张图片](http://img.e-com-net.com/image/info8/21fe14161c7943489cfcd30ecb415ccd.jpg)
![[译]背景:着色的物理和数学(1)_第13张图片](http://img.e-com-net.com/image/info8/20081382d06f41af8b0ea0d86197309a.jpg)
![[译]背景:着色的物理和数学(1)_第14张图片](http://img.e-com-net.com/image/info8/a2fb569347f5414fa873e4772282bfba.jpg)
![[译]背景:着色的物理和数学(1)_第15张图片](http://img.e-com-net.com/image/info8/83a3778464384e60925d8774cc63b48a.jpg)
![[译]背景:着色的物理和数学(1)_第16张图片](http://img.e-com-net.com/image/info8/17d8ecddc7d541c488c263b2c0ab2e38.jpg)
![[译]背景:着色的物理和数学(1)_第17张图片](http://img.e-com-net.com/image/info8/2acc4a3c299d46df8e869a47787cb01f.jpg)
![[译]背景:着色的物理和数学(1)_第18张图片](http://img.e-com-net.com/image/info8/70e4bbe057094504bba02071b310fe6d.jpg)
![[译]背景:着色的物理和数学(1)_第19张图片](http://img.e-com-net.com/image/info8/da2e01dce209422492b4580d03dfec2c.jpg)
![[译]背景:着色的物理和数学(1)_第20张图片](http://img.e-com-net.com/image/info8/26ae5d15c96443f8805428104b2b17b3.jpg)
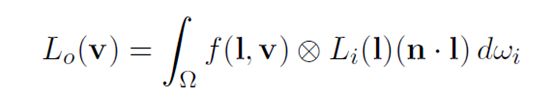
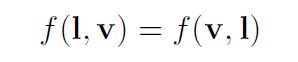

![[译]背景:着色的物理和数学(1)_第21张图片](http://img.e-com-net.com/image/info8/22853db0bfa5408980fba6fa388d46cd.jpg)